初等数论基础：积性函数的定义和性质证明

积性函数是数论中一类常用函数.本节介绍这类函数的一些初等性质及其应用.

定义2.2.1　定义在正整数集上而取值在复数集内的函数f（x）称为积性函数，若

（1）存在正整数a使得f（a）≠0，

（2）对任意两个互素的正整数a，b，有f（ab）=f（a）f（b）.

例2.2.2　对任意给定的实数λ，定义在正整数集上的函数fλ（a）=aλ是积性函数.

命题2.2.3　设f（x）是积性函数.则f（1）=1.

证明　由f（x）是积性函数知存在正整数a使得f（a）≠0.注意到（a，1）=1，有

f（a）=f（a·1）=f（a）f（1）.

这就导致f（1）=1.证毕.

命题2.2.4　设f1（x），f2（x）均为积性函数.则f（x）=f1（x）f2（x）也是积性函数.

证明　据命题2.2.3知f（1）=f1（1）f2（1）=1.设正整数a，b互素.则

f（ab）=f1（ab）f2（ab）=f1（a）f1（b）f2（a）f2（b）

=［f1（a）f2（a）］［f1（b）f2（b）］=f（a）f（b），

故结论成立.证毕.

定理2.2.5　设f（x）是积性函数，a是大于1的整数且其标准分解式为a=则

其中求和号表示对a的一切正因数求和.

证明　据命题1.4.14知a的一切正因数为

注意到=1（i≠j），有

据命题2.2.3知=f（1）=1.故结论成立.证毕.

推论2.2.6　设大于1的整数a的标准分解式为则a的所有正因数的和为(www.xing528.com)

而a的正因数的个数为

τ（a）=（α1+1）（α2+1）…（αn+1）.

证明　据例2.2.2知定义在正整数集上的函数f1（a）=a是积性函数.由定理2.2.5，有

而据例2.2.2知定义在正整数集上的函数f0（a）=a0=1是积性函数.由定理2.2.5，有

=（α1+1）（α2+1）…（αn+1）.

推论2.2.7　设a，b是正整数且（a，b）=1.则τ（ab）=τ（a）τ（b），S（ab）=S（a）S（b）.这表明τ和S是积性函数.

例2.2.8　由于28=22×7，故

作为上面结果的应用，本节剩余部分介绍梅森素数和完全数并揭示它们之间的紧密联系.首先定义梅森素数.这是以法国数学家梅森（Mersenne，1588—1648）的名字命名的一类有趣整数.为此，先给出以下事实.

命题2.2.9　若a，n是正整数，n＞1且an-1为素数，则a=2且n是素数.

证明　若a＞2，则（a-1）|an-1且1＜a-1＜an-1，这与an-1为素数矛盾.若a=2且n=kl，1＜k，l＜n，则2k-1|2n-1且1＜2k-1＜2n-1，这也与an-1为素数矛盾.证毕.

定义2.2.10　称形如2p-1的素数为梅森素数.由上述命题2.2.9知，若2p-1为梅森素数，则p必为素数，例如3，7都是梅森素数.称正整数n为完全数，若S（n）=2n.例如，6，28均为完全数.

关于梅森素数和完全数，有以下重要结果.

定理2.2.11（欧几里得-欧拉）　设q=2p-1为梅森素数.则

是完全数.反之，任何偶完全数均可如此构造.

证明　据推论2.2.7知

故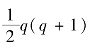为完全数.反之，设a是偶完全数.若a=2n，n≥1，则矛盾.故可记据推论2.2.7及a是完全数知

故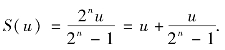但u及　皆为u之正因数，而S（u）为u的所有正因数之和，这表明u只有两个正因数，故u是素数且于是u=2n-1是梅森素数，从而n是素数且a=2n-1u.证毕.

注2.2.12　公元前6世纪的古希腊数学家毕达哥拉斯（Pythagoras，约公元前580—前500）是最早研究完全数的人，他已经知道6和28是完全数.定理2.2.11的正面部分是欧几里得在《几何原本》中证明的；而其反面部分则是欧拉证明的.另一方面，梅森首先对形如2p-1的素数展开系统研究.为纪念他，就把形如2p-1的素数称为梅森素数.由于梅森素数和完全数的重要联系以及在其他领域的广泛应用，千百年来一直吸引着众多数学家和无数的数学爱好者对它进行探究.但梅森素数在正整数中的分布异常稀疏，截止到2020年5月，一共才发现51个梅森素数.据定理2.2.11，也就有了51个完全数，这些完全数均为偶数.是否存在奇完全数是数论中一个未解决的难题.