初等数论基础：高斯函数及数论推论的应用

本节介绍高斯（Gauss）取整函数［x］的基本性质及其在求正整数标准分解式等方面的应用.

定义2.1.1　设x∈R.以［x］表示不超过x的最大整数，并称其为x的整数部分，而称｛x｝=x-［x］为x的小数部分.例如，

容易看出，对任意x∈R，有0≤｛x｝＜1.

下面的命题是容易验证的.

命题2.1.2　设x，y∈R，m∈Z.

（1）若x≤y，则［x］≤［y］.

（2）若m≤x＜m+1，则［x］=m.

（3）x-1＜［x］≤x＜［x］+1.

（4）［m+x］=m+［x］.

（5）［x］+［y］≤［x+y］≤［x］+［y］+1.

例2.1.3　求实数x使得2［x］+5x-31=0.

证明　据命题2.1.2（3）知x-1＜［x］≤x.故解之得从而［x］=4，进而有解毕.

命题2.1.4　设a，b是正整数.则不超过a且为b的倍数的正整数的个数为

证明　若a＜b，则结论显然成立.当a≥b时，在1，2，…，a中，能被b整除的数有

故结论成立.证毕.

例2.1.5　不大于350且为23的倍数的正整数的个数为　

下面考虑高斯函数在求某些整数的标准分解式中的应用.为此，需要一个预备结果.

命题2.1.6　设x∈R，n是正整数.则　

证明　据命题2.1.2（3）知　于是

进而有由命题2.1.2（2）知结论成立.证毕.

推论2.1.7　设m，a，b是正整数.则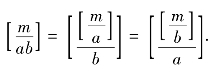

设m是正整数，p是素数.记m的标准分解式中素因数p的指数为Ep（m）.例如，18的标准分解式为18=2×32.故E2（18）=1，E3（18）=2，E5（18）=0.(www.xing528.com)

定理2.1.8　设n是大于1的整数，p是素数.则

证明　当p＞n时，p不可能整除n！，故此时Ep（n！）=0.下设p≤n.此时，从1到n这n个数中能被p整除的是p，2p，…于是

据推论2.1.7，有于是

依次类推便得

推论2.1.9　设n是大于1的整数.则

例2.1.10　求30！的标准分解式.

解　不大于30的素数有2，3，5，7，11，13，17，19，23，29.按定理2.1.8可分别求出这些素因数在30！的标准分解式中的指数分别为26，14，7，4，2，2，1，1，1，1.于是

30！=226×314×57×74×112×132×17×19×23×29

就是30！的标准分解式.解毕.

例2.1.11　求最大的正整数k使得10k|199！.

解　注意到10=2×5及E2（199！）＞E5（199！），有k=E5（199！）.故k=47.解毕.

推论2.1.12　设n=n1+n2+…+ns，其中ni是正整数，i=1，2，…，s.则是整数.

证明　据推论1.4.11，只需证明对任意素数p，有

Ep（n！）≥Ep（n1！n2！…ns！）=Ep（n1！）+Ep（n2！）+…+Ep（ns！）.

事实上，据命题2.1.2（5），对任意正整数j，有

据定理2.1.8，结论成立.证毕.

注2.1.13　推论2.1.12也可用组合方法证明.事实上，设想有n个带有标记的球和s个盒子.现在要把这n个球装到这s个盒子当中，其中第1个盒子有n1个球，第2个盒子有n2个球，…，第s个盒子有ns个球.容易验证，上述装球的方法总数就是　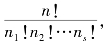这当然证明了它是整数.

推论2.1.14　设m是正整数.则m个连续整数的乘积能被m！整除.

证明　只需对m个连续正整数的情形进行证明.设这m个正整数为n+1，n+2，…，n+m，其中n是非负整数.当n=0时结论显然成立.若n＞0，则据推论2.1.12，

是整数，从而m！|（n+1）（n+2）…（n+m）.证毕.