趣味数独游戏：小学生入门级简史

数独是当今世界上广为流行的一种数学填数字益智游戏，其名称来自日本语すぅとく（Sudoku），意思是“独立的数字”或“在规定范围内只出现一次的数字”，概括来说，它就是一种填数字游戏。它与中国古代的“九宫格”游戏具有如出一辙的渊源关系。这种在欧美流行多年的数独，近年来在我国逐渐开展与普及，有不少人对此着迷。数独玩法很简单，拿起纸和笔就能玩数独，有的在计算机上或上网玩数独，甚至还可以拿着手机玩数独游戏。有的报刊上几乎天天都登有数独题；有的地方还出现了有关数独的爱好者组织（如数独联盟等），国际上还成立了国际数独联盟，每年都会组织国际数独比赛。由此可见数独游戏在世界上普及的程度。

追溯数独的起源，早在4000年前我国就可看到它的影子。它的基本结构就是九宫格，即带有9个方格的九宫图。传说在上古时期（约在公元前21世纪初）大禹治水的时候，洛河里出现了一只乌龟，在龟背上画有一幅图，人们称其为“洛书”，它由许多圆点组成图形，如图1-1所示。该图形共有45个圆点（或圈点），分别组合成方形。东、西、南、北各为7、3、1、9个圆点；四角各为8、6、2、4个圆点；中间则为5个圆点。

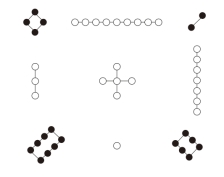
图1-1

到了北周（557—581年）时，易学家把它和九宫图联系起来，即将八卦和中央之宫合起来，称作九宫。于是，在当时的数学中就出现了用数字代替圆点数的九宫图，即带数的九宫格。而且在书中列有数的排列法，北周甄鸾注解道：“二四为肩，六八为足，左三右七，戴九履一，五居中央”，如图1-2所示。到了宋朝（960～1279年），开始出现了“重排九宫”游戏。这就是格子数字游戏的起源。

图1-2

但是，应该指出，中国古代的九宫图与现代的数独只是外形上的相似，而在内容上是不同的。其实中国古代的九宫图体现的是现代数学书中的“幻方”，它的规律是每行、每列以及两条对角线上的各数之和相等；而标准数独是由9个九宫组成一个阵，它要求每行、每列以及每个九宫格内的数1～9不重复。例如，在我国发现有一张古代的藏宝图，这张藏宝图被藏宝的主人刻意地分成了杂乱无章的9块图形，令人莫名其妙，幸好在这些图形的背面都分别标注有等数字。如何将这9个标有分数的图形正确地放入图1-3中，使填入的格子中的每一行、每一列、两条对角线上3个格子中的数字之和都相等，这样就可得到一张完整无缺的藏宝图。

图1-3

解题的方法：第一步，将9个数字相加，得到

第二步，将，说明每一行、每一列、每一条对角线上3个数字之和都等于。

第三步：将分成9个数，分别填入相应的方格中，将图1-4中分数化简后得如图1-5的藏宝图。

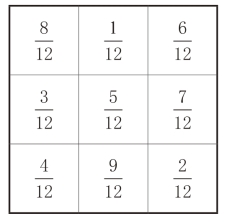
图1-4

图1-5

由此可见，中国古代的九宫图与现代的数独有着本质上的区别。但是，在中国古代的九宫改造变成现代的数独的漫长历史长河中，有一个变化的突破点，就是18世纪80年代的瑞士数学家里昂哈德·欧拉（Leonhard euler）的“拉丁方”，这也就是现代数独的起源。

当时欧洲有个普鲁士王国（PRUSSIA，1871年以普鲁士为中心建立了统一的德意志帝国）。据说，有一年，这个王国的国王腓特烈举办阅兵式。他计划从6支部队中各选6名官兵，组成36人的方队，作为阅兵的先导部队。组队的要求是各部队的6名官兵分别是少尉、中尉、上尉、少校、中校、大校各一名。而且这36名官兵要组成一个方阵，方阵中每一行、每一列都有各部队、各级别的官兵各一人。(www.xing528.com)

怎样才能排出这样的方阵呢？当时著名的瑞士数学家欧拉正在普鲁士王国的柏林，于是国王请他来帮忙解决这一难题。欧拉绞尽脑汁采用各种方法也没有排出这6×6的36人方阵来。可是在1782年他排出了3×3的9人方阵。他用拉丁字母A、B、C来代表不同级别的官兵，然后将这些字母填入九宫中，如图1-6所示。按照该3×3的九宫格完全符合国王腓特烈的要求。由于在该方阵中使用了希腊和拉丁字母，后人称其为“希腊·拉丁方”。

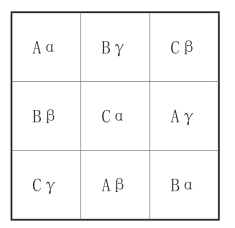
图1-6

我们可以把图1-6中的A、B、C和α、β、γ分别用1、2、3代替，排成两个九宫，如图1-7和图1-8所示。由图可见，这两个九宫格中数的排列就接近现代的数独规定了。因此。有人认为，拉丁方是数独的雏形。当然，它也只能是数独的雏形，因为它的九宫格还没有组成九九相连的现代数独的阵式。

图1-7

图1-8

真正意义上的数独，出现在20世纪70年代。1979年5月，美国的一本《数学逻辑》杂志上第一次发表了两道数学智力游戏题，当时名为Number place（数字排位），这个游戏题类似于现在的数独。这两道最早的数独题如图1-9和图1-10所示，它由9个相连的九宫的格内都含有1至9这9个数。掌握了这一规定，就能帮助你顺利地做出答案。下面两道题中各有四个画有圆圈的方格，你可以把它们当作填数的首选，不过并非一定如此。题目下还附有答案的范围。

图1-9

图1-10

那么，这两道最早的数独题是谁创造出来的呢？据说原作者叫哈瓦德·冈恩（Howard Garn），他是一位退休的建筑设计师，已于1989年去世，这两道题是他74岁时创作的。

可是，这两道题当时在美国并未产生很大的影响，倒是后来被一位日本学者引进日本，在日本引起了重视。1984年4月，日本《益智游戏》杂志《Puzzle Tsushin Nikoli》员工金元信彦接触到美国猜谜书上某版本的数字游戏，认为可以用来吸引读者的眼球，便对其进行改进且增加难度，在该杂志上首先刊登了此类难题，并取名为数独（Sudoku），意思是“独立的数字”，推出后一炮打响。

真正把数独推向世界的是新西兰韦恩·古德（Wayne Gould），他曾是一位在香港高等法院任职的法官。1997年3月的一天，退休的古德到东京去旅游，晚上住在酒店里，随手翻看杂志，无意中看到了杂志上登载的数独游戏。他饶有兴趣地算了一个晚上，深深地迷上了这种数独游戏。从那以后，古德用了6年的时间，设计了数独游戏的计算机程序，还创立了一个提供这种游戏的网站，来自世界各国的网友光顾了他的网站，据说该网站的点击率相当高。为了进一步提高点击率，提升人气，必须与传统媒体合作。古德找到了英国的一些媒体，可是开始并不顺利。终于有一天，有名的《泰晤士报》决定试试看，主编迈克尔·哈维接见了古德，古德向他展示了数独的玩法，嗅觉灵敏的主编在几分钟内就意识到这是一种令人叫绝的游戏，他迅速下了决定，英国《泰晤士报》于2004年11月12日首次刊登数独，并进行连载，引起了人们极大的关注与兴趣，成为全球最疯狂的数字迷宫，进而引发了一场声势浩大的“数独”热，在短短的数月间便蔓延至全球，成为人们非常喜爱的一种智力数字游戏。

在《泰晤士报》刊登后仅隔两天，《每日邮报》就跟进了，随后英国有名的报纸如《每日电讯报》《独立报》《卫报》纷纷刊登了有关数独的内容，这些报纸在英国乃至全世界都具有很大的影响力。接着全球有数十家日报相继刊登数独，有些甚至放在头版上。有了这些媒体的支持，数独这回真正走向了全世界。

这股风很快又吹到了美国，想不到这种“出口转内销”的游戏在美国兴起了新浪潮。不仅各种杂志、报纸争先刊登，而且各种数独书不断推出，更有各种数独组织和沙龙纷纷出现。据不完全统计，美国市场上流行的数独书有150多种，各种专门的数独杂志遍布大小超市，而且有不少美国人视数独为日常“用品”。