OFDM与多载波传输在室内可见光通信中的研究

3.2.1　单载波基带传输系统模型

单载波基带传输系统如图3.1所示[2，3]。信源产生符号序列{am}，通过发送滤波器 gTx（t），对传输符号进行脉冲成形，假设符号周期为T。信号经过带宽为W的传输信道 h（t）。信号被接收后，再分别通过接收滤波器和均衡器，最后抽样判决后恢复信号。用 gTx（t）、gRx（t）和h-1（t）分别表示发射滤波器、接收滤波器和均衡器的冲激响应。

图3.1　单载波基带通信系统模型

均衡器的输出信号表示为

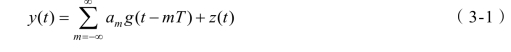
其中，z（t）为加性噪声，g（t）为系统的冲激响应。

假设接收端能准确估计信道特性，并能够补偿信道的影响。那么系统的冲激响应只受发送滤波器和接受滤波器的影响。当忽略噪声项时，均衡器的采样输出信号可以表示为

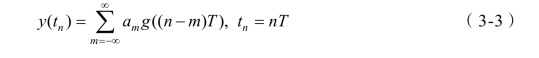
其中第n个抽样值 an表示为

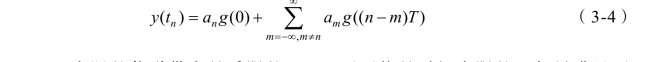
实际的信道带宽是受限的，g（t）不可能是时间有限的。如果满足不等式 g（（n-m）T）≠0，∀m≠n，那么式（3-4）中的第2项将会对 an产生符号间干扰（ISI）。符号间干扰由系统冲激响应的拖尾引起，会降低数字通信系统的性能。为了尽量降低或彻底消除 ISI，必须仔细设计接收滤波器和发射滤波器。图3.2所示为由系统冲激响应拖尾引起抽样信号ISI的示意图。可以看出，符号周期T决定了ISI的大小。符号周期越短，ISI的影响越大。这意味着，在单载波传输系统中，除非g（（n-m）T）=0，∀m≠n，否则，当数据速率增大时（即在图3.2中减小T），ISI会变得十分严重。

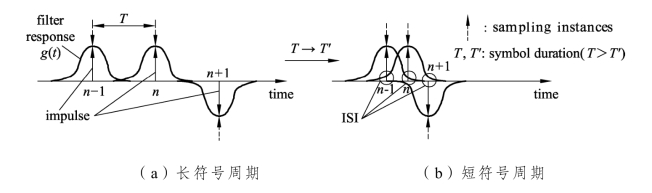
图3.2　ISI和符号周期的示意图

只要系统冲激响应满足下面的时域条件，就可以彻底消除ISI。

式（3-5）的时域冲激响应对应的频域响应为

其中 G（f）为 g（t）的傅立叶变换。式（3-5）或者式（3-6）的条件被称为奈奎斯特准则。只要满足奈奎斯特准则，就能保证在单载波系统中进行高速数据传输无ISI的影响。满足奈奎斯特准则的滤波器称为奈奎斯特滤波器。

理想的低通滤波器（LPF）冲激响应是sinc函数，就是奈奎斯特滤波器。频域响应表示为(www.xing528.com)

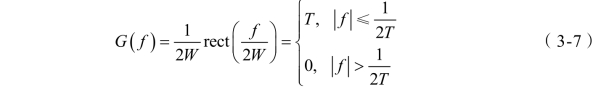
其中W=R/2=1/（2T）。在式（3-7）中，R和W分别对应奈奎斯特速率和奈奎斯特带宽。数据速率为R，不受ISI影响，所需的最小带宽W被称为奈奎斯特带宽。然而，理想的LPF滤波器在物理上是不可实现的，因为其冲激响应不是因果的[即在t＜0的情况下，g（t）≠0，并且持续时间是无限的]。

另一个物理可实现的奈奎斯特滤波器是升余弦滤波器，频率响应为

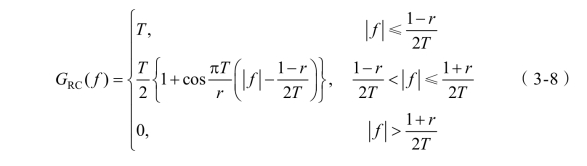
其中，r为滚降系数，取值范围为0≤r≤1。式（3-8）满足无ISI条件，但没有理想低通滤波器的频域响应那样陡峭。升余弦滤波器的脉冲响应占用的频带大于奈奎斯特带宽，实际带宽由滚降系数r决定。图3.3所示为滚降系数r为0、0.5、1时，升余弦滤波器的冲激响应和频率响应。在r=0时，升余弦滤波器与理想LPF的带宽相同。在r=1时，其带宽是奈奎斯特带宽的2倍。

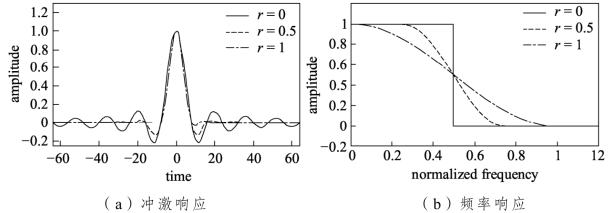
图3.3　升余弦滤波器

3.2.2　高速单载波传输的挑战

为了支持每秒传输 Rs个符号的速率，所需的最小传输奈奎斯特带宽为 Rs/2Hz。这意味着在单载波传输系统中，需要很大的传输带宽来支持更高的数据速率。信号带宽随着符号速率的增大而增大。当信号带宽大于无线信道的相干带宽时，信号会受到频率选择性衰落的影响，从而会产生ISI。假设均衡器能够完美补偿信道的影响。利用自适应均衡器，可以处理由时变多径衰落信道引起的ISI。但是，随着数据速率的增大，均衡器的复杂度增加。例如，用有限冲激响应（FIR）滤波器来实现自适应滤波，通过自适应调整抽头系数，可以将ISI的影响降低到最小。事实上，数据速率越大，ISI的影响越明显，所需的均衡器抽头越多，均衡器的实现复杂度越大。

在多径衰落信道中，最大似然序列检测器（MLSD）是最优的ML检测器，M表示调制符号阶数，L表示在多径衰落信道上产生的ISI跨度。根据在连续符号间隔内接收到的符号序列的观察值，以最大化后验概率做出判决。它的复杂度取决于调制阶数和多径数。因为ISI跨度的记忆长度为L，所以为相应的欧式距离的度量，用于在MLSD中选择最佳的序列。通过增大M，可以实现更高的数据速率，但是最优均衡器的复杂度将变得不可接受。例如，在时延扩展为10μs的多径衰落信道上，调制采用64-QAM，数据传输速率为10Mb/s，则 L=16，ML=6416。另外，当M和L较大时，可以使用更加实用的次优均衡器，如最小均方误差（Minimum Mean Square Error，MMSE）和最小二乘（Least Square，LS）均衡器。然而，ISI随着数据速率的增大而增大，次优均衡器仍然由于复杂度太大而无法实现。这是因为当信道频率的选择性增加时，均衡器的频率响应变得更加陡峭。总之，由于接收机的均衡器过于复杂，高数据速率的单载波传输实现困难。

3.2.3　多载波传输方案

为了克服宽带信道频率选择性对单载波传输的影响，可以使用多载波实现高数据速率传输。图3.4给出了多载波传输系统的基本结构和概念。在发射机端，通过多个窄带滤波器Hk（f），将宽带信号分解为若干个窄带信号。在接收机端，通过多个窄带滤波器 Gk（f）[每一个与Hk（f）匹配]，再将这些窄带信号合成。将有频率选择性衰落的宽带信道划分为若干个具有频率平坦衰落的窄带信道，从而降低了子信道上实现均衡器的复杂度。只要能够保持子信道间的正交性，就可以抑制载波间干扰（ICI），从而可以实现无失真的传输。

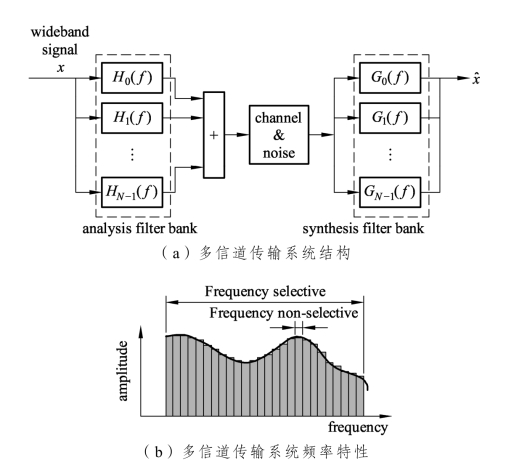
图3.4　多信道传输系统的结构和频率特性

3.2.4　OFDM传输方案

正交频分复用（OFDM）传输方案是多信道系统的一种，如图3.5（a）所示，OFDM有多个子载波，每个子载波信道不需要使用独立的滤波器和振荡器。为了提高带宽效率，子载波的频谱相互重叠，将式（3.6）中单载波的奈奎斯特准则推广到多载波的准则，可以产生频域上重叠的正交子载波信号。在实现时，采用离散傅立叶变换（DFT）和离散傅立叶逆变换（IDFT）。通过快速傅立叶（FFT）和快速傅立叶逆变换（IFFT）可以快速实现DFT和IDFT。图3.5（b）给出了由IDFT/DFT实现的OFDM传输结构。在OFDM传输系统中，对发射信号 Xl[k]，k=0，1，…，N-1，采用N点IFFT，可以生成 x[n]，n=0，1，…，N-1，它们是对N个子载波信号之和的采样。令 y[n]表示接收信号的采样，y[n]=w[n]+x[n]，w[n]表示加性噪声。在接收机端，采用N点FFT，可以得到包含噪声的发射信号。如图3.5（c）所示，当所有子载波的持续时间T有限时，可以认为OFDM信号的频谱是经过频移的sinc函数在频域上的总和，其中所有重叠的相邻sinc函数的间隔是1/T。

因为每个符号上的每个子载波信号都是时间有限的（不是带宽有限的），所以 OFDM信号会产生带外辐射，这将引起不可忽略的邻道干扰（Adjacent Channel Interference，ACI）。从图3.5（d）可以清楚地看到，频谱的第一旁瓣与主瓣相比较大。因此为了减少带外辐射，OFDM方案在外侧的子载波上设置了一个保护带宽，被称为虚拟子载波（Virtual Carrier，VC）。为了更好地消除OFDM符号间的ISI，OFDM系统在时域间隙插入保护间隔，称为循环前缀（Cyclic Prefix，CP）。

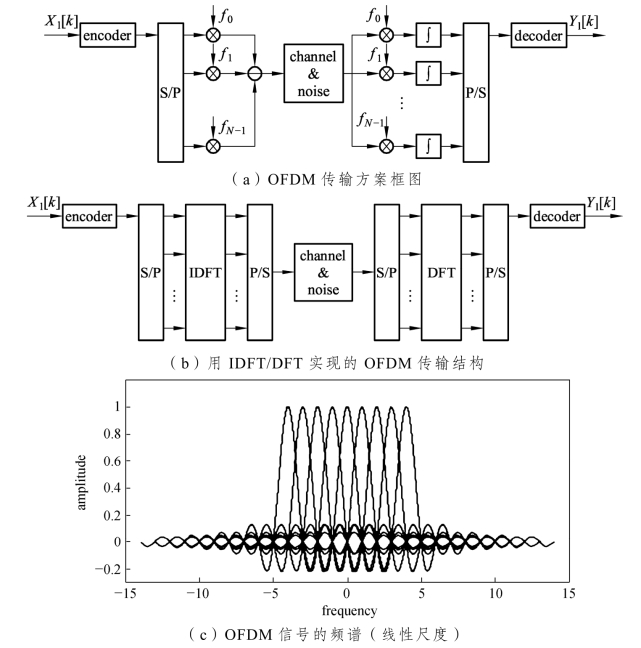
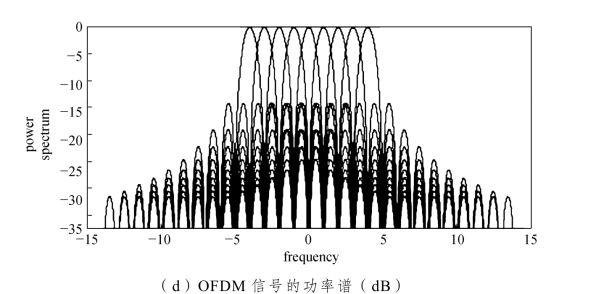
图3.5　OFDM传输方案的结构和频谱特征