数据分析：柳钢矿渣和粉煤灰胶凝材料的最佳掺量研究

1.数据分析方法

正交试验结果的极差分析包括以下4个方面的内容：

（1）分析因素与抗压强度的关系。根据试验结果计算每个因素水平相同的各次试验结果的均值K，并绘制各种因素与抗压强度的趋势图，从而分析各因素的水平变化时抗压强度的变化规律。

（2）分析因素影响抗压强度的主次关系。计算各因素的极差R，确定各个因素对指标影响的主次顺序。

（3）分析比较计算结果，挑选水平最佳的因素组合，即这3个因素各取什么水平时，抗压强度最高。

（4）通过综合分析，确定最优配合比，为下一步试验指出方向。

其中，极差R指的是各列中各个水平对应的试验指标平均值的最大值和最小值之差。极差的大小反映了试验中的相应因素对指标作用的显著性。极差大的因素，意味着其不同水平给指标所造成的影响较大，通常是主要因素；极差小的因素，意味着其不同水平给指标所造成的影响比较小，通常是次要因素。

2.正交试验分析

（1）正交试验3d数据分析。

L16（45）正交试验的3d抗压强度极差分析，见表4.1.4。

表4.1.4　正交试验3d抗压强度极差分析表

从3d抗压强度极差分析表4.1.4可以看出，激发剂NS的极差R为12.35，相对影响最大，说明激发剂NS是影响矿渣胶凝材料3d强度的最主要因素；NL的极差为12.15，影响次之；NH的极差为4.17，相对影响最小。由此可知，复合激发剂中各个组分对矿渣胶凝材料的3d抗压强度影响的主次顺序为：A＞B＞C。

根据表4.1.4数据，对于数量性水平的四水平的因素，以因素NS、NL、NH各水平实际值作为横坐标，以K值为纵坐标，对应作图，如图4.1.1～图4.1.3所示。

图4.1.1　3d抗压强度NS掺量与K值直观分析图

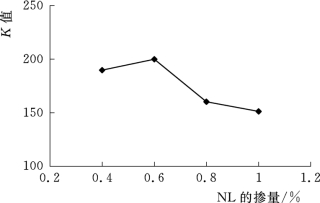
图4.1.2　3d抗压强度NL掺量与K值直观分析图

图4.1.3　3d抗压强度NH掺量与K值直观分析图

由表4.1.4的计算和图4.1.1～图4.1.3可以看出各因素所绘制的趋势图均存在一个峰值，又因为以抗压强度作为评价胶凝材料的指标，故选取最大抗压强度相对应各因素的水平作为最佳的配方。从图4.1.1～图4.1.3分析得知，NS掺量以A3=4%强度最好；NL掺量以B2=0.6%为最好；NH掺量以C3=0.6%为最好。

（2）正交试验7d数据分析。

L16（45）正交试验的3d抗压强度极差分析，见表4.1.5。

表4.1.5　正交试验7d抗压强度极差分析表

L16（45）正交试验的7d抗压强度极差分析，见表4.1.5。从7d抗压强度极差分析表可以看出，激发剂NS的极差R为13.42，相对影响最大，说明激发剂NS是影响矿渣胶凝材料7d强度的最主要因素；NL的极差为11.54，影响次之；NH的极差为2.55，相对影响最小。由此可知，复合激发剂中各个组分对矿渣胶凝材料的7d抗压强度影响的主次顺序为：A＞B＞C。

图4.1.4～图4.1.6给出了7d抗压强度随复合激发剂中各个因素水平变化的直观趋势图。

图4.1.4　7d抗压强度NS掺量与K值直观分析图

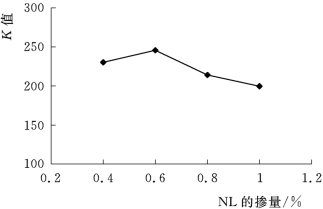
图4.1.5　7d抗压强度NL掺量与K值直观分析图

与3d抗压强度的各因素趋势图类似，图4.1.4～图4.1.6中也存在着一个峰值，NS掺量以A3=4%强度最好；NL掺量以B2=0.6%为最好；NH掺量以C2=0.6%为最好。(www.xing528.com)

（3）正交试验28d数据分析。

L16（43）正交试验的28d抗压强度极差分析，见表4.1.6。

从28d抗压强度极差分析表4.1.6可以看出，激发剂NS的极差R为15.37，相对最大，说明激发剂NS是影响矿渣胶凝材料28d强度的最主要因素；NL的极差为13.23，影响次之；NH的极差为3.85，相对最小。由此可知，复合激发剂对胶凝材料28天强度影响的主次顺序为：A＞B＞C。

图4.1.6　7d抗压强度NH掺量与K值直观分析图

表4.1.6　正交试验28d抗压强度极差分析表

图4.1.7　28d抗压强度NS掺量与K值直观分析图

图4.1.7～图4.1.9给出了28d抗压强度随复合激发剂中各个因素水平变化的直观趋势图。

与7d抗压强度的各因素趋势图类似，NS掺量以A3=4%强度最好；NL掺量以B2=0.6%为最好；NH掺量以C2=0.6%为最好。

对照表4.1.4～表4.1.6，对应于每一因素Ki达到最高的水平，可以粗略地判断出各种因素的优化取值，由此可以选出各因素的最佳组合为A3B2C2。

图4.1.8　28d抗压强度NL掺量与K值直观分析图

图4.1.9　28d抗压强度NH掺量与K值直观分析图

（4）正交设计的直观分析简单直观，是一种常用的方法。但直观分析在分析前要做误差较小的假定，而实际中往往并非如此，因此就不能给出试验误差大小的估计，更不能给出分析精度的估计。为了判断和排除试验误差造成的错觉，还需进一步进行正交试验的方差分析。从直观分析可以看到，各种因素对3d、7d和28d强度的影响具有大致相同的规律，为了简化问题起见，我们以28d强度指标作为方差分析的判断。

1）计算各因素及总的试验数据平方和。

类推可得：S4=21.19，S5=8.38。

2）计算误差平方和。

表4.1.2中第4、5列为空列，因此S误=S4+S5=29.57。

3）确定自由度。

构成平方和的独立变量的个数称为自由度，分别用f总、fA、f误来表示S总、SA、S误的自由度。如果平方和由n项组成，总的自由度就等于n-1；如果一个平方和由n部的平方和组成，则总的自由度等于各部分自由度之和，由此得出：

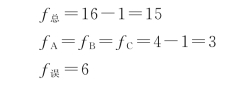
4）显著性检验。

我们将S总/f总、SA/fA、SB/fB、SC/fC、S误/f误称为平均平方和或方差。但是因素引起的波动与方差引起的波动大小还不能断定某因素影响的显著性，根据数理统计，只要将比值与Fa（fi·f误）值进行比较就可以得出以下结论。当FA≥Fα（fA·f误），即SA/fA比S总/f总大得多时，我们就说因素A对指标的影响是显著的。Fα（fA·f误）叫做临界值，α叫做显著性水平，通常α=0.01、α=0.05、α=0.25。如果取α=0.01，也就是说，我们有1-α=1-0.01=0.99=99%的把握说该因素影响是否显著。

查F分布表可知，F0.01（3，6）=9.78，F0.05（3，6）=4.76，故因素A、B作用高度显著，因素C作用不显著，这与直观分析结果分析结果相一致，其优化参数的选择与直观分析方法相同。

显著性方差分析见表4.1.7。

表4.1.7　显著性检验方差分析