1.设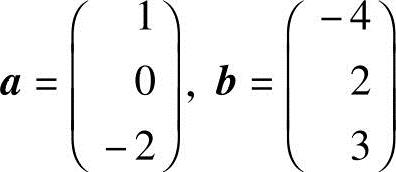 ,c与a正交,且b=λa+c,求λ和c.
,c与a正交,且b=λa+c,求λ和c.
解 以aT左乘题设关系式得
aTb=λaTa+aTc,
因a与c正交,有aTc=0;a≠0,有aTa≠0,故得
从而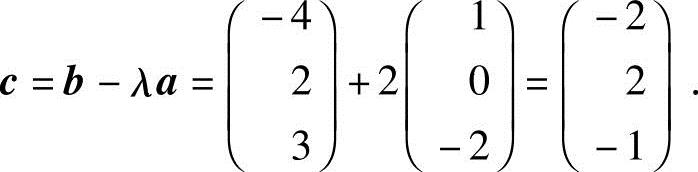
2.试用施密特法把下列向量组正交化:
解
3.下列矩阵是不是正交矩阵?并说明理由:
解 (1)不是,因为第1个列向量不是单位向量;
(2)是,因为此矩阵的3个列向量构成规范正交基,即它们两两正交,并且都是单位向量.
4.设x为n维列向量,xTx=1,令H=E-2xxT,证明:H是对称的正交阵.
证 对称性:HT=(E-2xxT)T=E-2xxT=H.
正交性:HTH=H2 (由H的对称性)
=(E-2xxT)(E-2xxT)
=E-4xxT+4(xxT)(xxT)
=E-4xxT+4x(xTx)xT=E (由xTx=1).
5.设A与B都是n阶正交阵,证明:AB也是正交阵.
证法一 因(AB)(AB)T=(AB)(BTAT)
=A(BBT)AT
=AAT (由BBT=E)
=E (由AAT=E),由定义,知AB是正交阵.
证法二 因A,B是正交阵,故A,B均可逆,且A-1=AT,B-1=BT.于是AB可逆,且有
(AB)-1=B-1A-1=BTAT=(AB)T,
从而AB是正交阵.
6.求下列矩阵的特征值和特征向量:
解 (1)A的特征多项式为
所以A的特征值为λ1=λ2=λ3=-1(三重根).
对于特征值-1,解方程(A+E)x=0.由
得对应的特征向量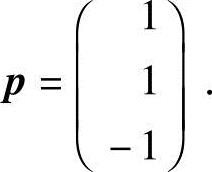
(2)A的特征多项式为
所以A的特征值为λ1=-1,λ2=0,λ3=9.
当λ1=-1时,解方程(A+E)x=0.由
得对应的特征向量 ;
;
当λ2=0时,解方程Ax=0.由
得对应的特征向量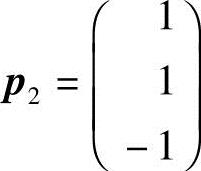 ;
;
当λ3=9时,解方程(A-9E)x=0.由
得对应的特征向量 .
.
(3)A的特征多项式为
所以A的特征值为λ1=λ2=-1,λ3=λ4=1.
当λ1=λ2=-1时,解方程(A+E)x=0.由
得对应的线性无关的特征向量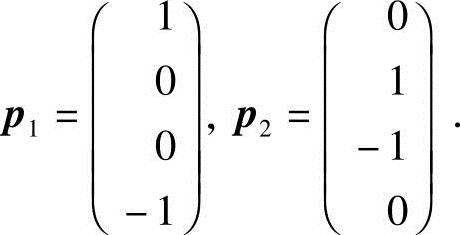
当λ3=λ4=1时,解方程(A-E)x=0.由
得对应的线性无关的特征向量
7.设A2-3A+2E=O,证明:A的特征值只能取1或2.
证 设λ是A的特征值,则λ2-3λ+2是A2-3A+2E=O的特征值.但是,零矩阵只有特征值0,故λ2-3λ+2=0得λ=1或λ=2.
注 本题并不是说A必须有特征值1和2,例如,当A=E时,满足题设条件,但A只有特征值1.
8.设A为正交阵,且|A|=-1,证明:λ=-1是A的特征值.
证 由特征方程的定义,
λ=-1是A的特征值⇔|A+E|=0,因此,只需证|A+E|=0.由A为正交阵,知ATA=E,则
|A+E|=|A+ATA|=|(E+AT)A|=|E+AT·A|=|(A+E)T|·|A|
=|A+E|·|A|=-|A+E|
⇒2|A+E|=0⇒|A+E|=0.
9.设λ≠0是m阶矩阵Am×nBn×m的特征值,证明:λ也是n阶矩阵BA的特征值.
证 根据特征值的定义证明.
设λ是矩阵AB的任一非零特征值,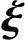 是对应于它的特征向量.即有
是对应于它的特征向量.即有
AB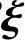 =λ
=λ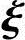 . (5-3)用矩阵B左乘上式两边,得
. (5-3)用矩阵B左乘上式两边,得
(BA)B =λ(B
=λ(B ),
),
若B ≠0,则由特征值定义知,λ是矩阵BA的特征值.下面证明B
≠0,则由特征值定义知,λ是矩阵BA的特征值.下面证明B ≠0.事实上,由λ≠0,特征向量
≠0.事实上,由λ≠0,特征向量 ≠0,有λ
≠0,有λ ≠0,再由式(5-3)得AB
≠0,再由式(5-3)得AB ≠0,因此B
≠0,因此B ≠0.
≠0.
10.已知3阶矩阵A的特征值为1,2,3,求|A3-5A2+7A|.
解 设φ(λ)=λ3-5λ2+7λ.因1,2,3是A的特征值,故φ(1)=3,φ(2)=2,φ(3)=3是φ(A)=A3-5A2+7A的特征值.又因为φ(A)是3阶方阵,于是φ(1),φ(2),φ(3)是φ(A)的全部特征值.由特征值性质得
|A3-5A2+7A|=|φ(A)|=φ(1)φ(2)φ(3)=3×2×3=18.
11.已知3阶矩阵A的特征值为1,2,-3,求|A*+3A+2E|.
解 由特征值性质,得|A|=1×2×(-3)=-6≠0,知A可逆,故A*=|A|A-1=-6A-1,并且
A*+3A+2E=-6A-1+3A+2E.
把上式记作φ(A),有φ(λ)=-6λ-1+3λ+2.因为当λ(≠0)为A的特征值时,-6λ-1+3λ+2是A*+3A+2E的特征值.分别取λ=1,2,-3知-1,5,-5是A*+3A+2E的特征值.注意到A*+3A+2E为3阶方阵,故|A*+3A+2E|=(-1)×5×(-5)=25.
12.设A,B都是n阶矩阵,且A可逆,证明:AB与BA相似.
证 因A可逆,故
BA=(A-1A)BA=A-1(AB)A,
由定义,AB与BA相似.
13.设矩阵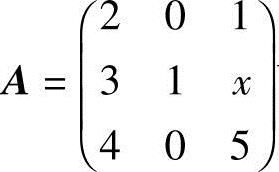 可相似对角化,求x.
可相似对角化,求x.
解 先求A的特征值
得 λ1=λ2=1(二重根),λ3=6(单重根).
对应单根λ3=6,可求得线性无关的特征向量恰有1个,故矩阵A可对角化的充分必要条件是对应重根λ1=λ2=1,有2个线性无关的特征向量,即方程(A-E)x=0有2个线性无关的解,亦即系数矩阵A-E的秩R(A-E)=1(由教材中第四章的定理4.7).由
要R(A-E)=1,得x-3=0,即x=3.因此,当x=3时,矩阵A能对角化.
14.已知 是矩阵
是矩阵 的一个特征向量.
的一个特征向量.
(1)求参数a,b及特征向量p所对应的特征值;
(2)问A能不能相似对角化?并说明理由.
解 (1)利用特征值和特征向量的定义.
设p所对应的特征值是λ,则由题设,(A-λE)p=0,即
于是,得到以a,b,λ为未知数的线性方程组
(2)A不能相似于对角阵.理由是:当a=-3,b=0时,求得矩阵A的特征多项式f(λ)=A-λE=-(λ+1)3,故λ=-1是A的三重特征值.但A+E≠O,从而R(A+E)≥1,故齐次方程(A+E)x=0没有3个线性无关的解.于是,矩阵A对应于特征值λ=-1没有3个线性无关的特征向量.由方阵相似于对角阵的充要条件(见教材中的定理5.6)知,A不能相似于一个对角阵.
15.设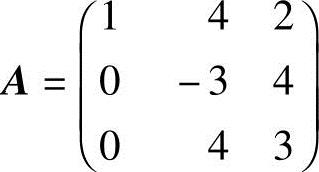 ,求A100.
,求A100.
解 利用矩阵A的相似对角阵来求A100.
(1)求A的特征值:
所以A的特征值为λ1=-5,λ2=1,λ3=5,并且它们各不相同,由教材中定理5.6之推论,知A可对角化.
(2)对应λ1=-5,解方程(A+5E)x=0.由
得对应的特征向量 ;
;
对应λ2=1,解方程(A-E)x=0.由
得对应的特征向量 ;
;
对应λ3=5,解方程(A-5E)x=0.由
得对应的特征向量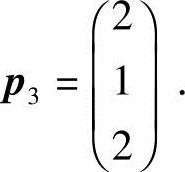
(3)令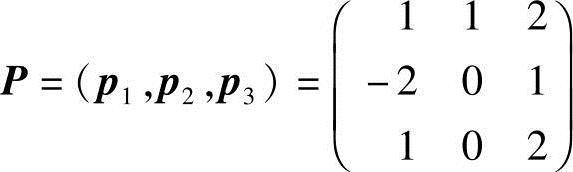 ,
,
则由定理5.4,P为可逆阵,且
于是 A=PΛP-1⇒A100=PΛ100P-1.
求出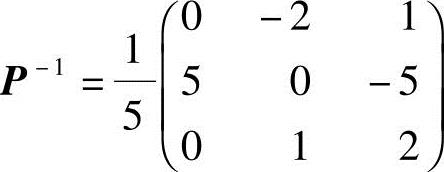 ,得
,得
16.试求一个正交的相似变换矩阵,将下列对称阵化为对角阵:
解 (1)先求特征值:
所以A的特征值为λ1=-2,λ2=1,λ3=4.
再求特征向量:
对应λ1=-2,解方程(A+2E)x=0.由
得基础解系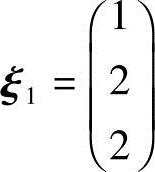 ,将
,将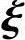 1单位化,得单位特征向量
1单位化,得单位特征向量 ;
;
对应λ2=1,解方程(A-E)x=0.由
得基础解系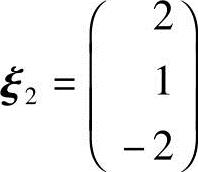 ,将
,将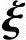 2单位化,得单位特征向量
2单位化,得单位特征向量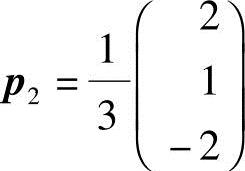 ;
;
对应λ3=4,解方程(A-4E)x=0.由
得基础解系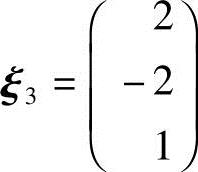 ,将
,将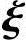 3单位化,得单位特征向量
3单位化,得单位特征向量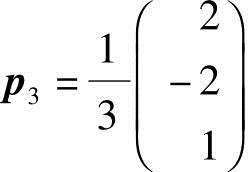
令 ,
,
则P为正交阵,且有
(2)先求特征值:
所以A的特征值为λ1=10,λ2=λ3=1(二重根).
再求特征向量:
对应λ1=10,解方程(A-10E)x=0.由
得基础解系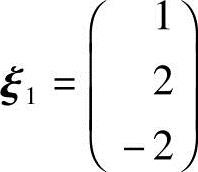 ,将
,将 1单位化,得单位特征向量
1单位化,得单位特征向量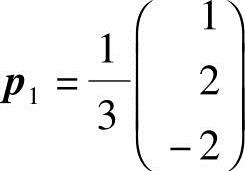 ;
;
对应λ2=λ3=1,解方程(A-E)x=0.由
得基础解系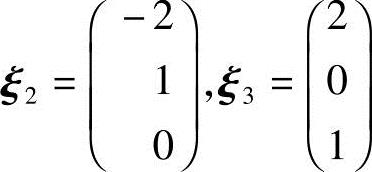 .将
.将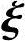 2,
2,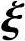 3正交化得:
3正交化得:
再将η2,η3单位化得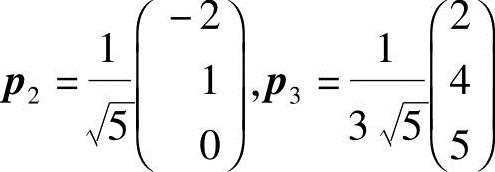 .
.
令
则P为正交阵,且有
17.设矩阵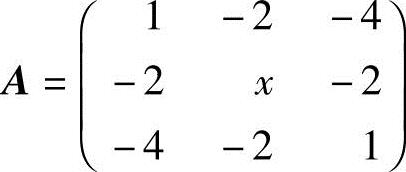 与
与 相似,求x,y;并求一个正交阵P,使P-1AP=Λ.
相似,求x,y;并求一个正交阵P,使P-1AP=Λ.
解 先求x,y.
因A与Λ相似,故A的特征值是5,-4,y.由特征值性质:
5+(-4)+y=A的特征值之和
=A的对角元之和=2+x得y=1+x.
因λ=-4是A的特征值,有A+4E=0.由
得x=4.再代入y=1+x,得y=5.于是A的特征值为λ1=λ3=5,λ2=-4.
再求正交阵P.
对应λ1=λ3=5,解方程(A-5E)x=0.由
得基础解系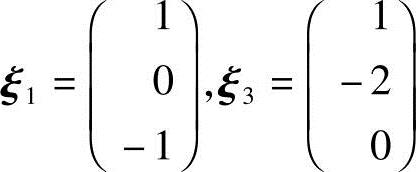 .将
.将 1,
1,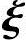 3正交化得:
3正交化得:
再将η1,η3单位化得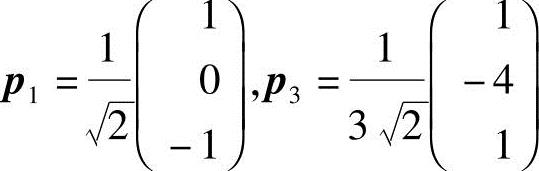 ;
;
对应λ2=-4,解方程(A+4E)x=0.由
得基础解系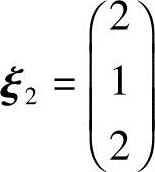 ,将
,将 2单位化,得单位特征向量
2单位化,得单位特征向量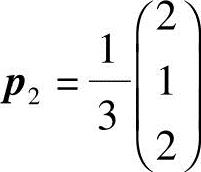 .
.
令 ,则P为正交阵,且有
,则P为正交阵,且有
注 (1)在寻找x,y的关系式时,题解中用了A的对角元之和=Λ的对角元之和以及|A+4E|=0,也可利用特征值的另一性质:|A|=A的特征值之积=Λ的特征值之积=|Λ|,得3x+8=4y.但由|A-5E|=0不能得到x,y的关系式,因|A-5E|≡0.
(2)因相似对角阵Λ是给定的,所以要注意P中列向量的排列必须与Λ中的对角元对应.
18.设3阶方阵A的特征值为λ1=2,λ2=-2,λ3=1;对应的特征向量依次为
求A.
解 因A的特征值互异,故由教材中的定理5.4,知向量组p1,p2,p3线性无关,于是,若记矩阵P=(p1,p2,p3),则P为可逆阵,且有
容易求得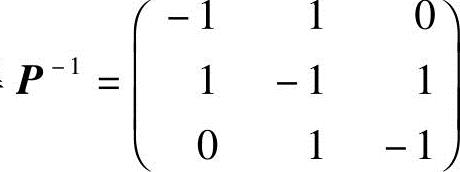 .于是
.于是
19.设3阶对称阵A的特征值为λ1=1,λ2=1,λ3=0;对应λ1,λ2的特征向量依次为
求A.
解 因A对称,故由教材中的定理5.9,必有正交阵Q=(q1,q2,q3),使
显然q1,q2可依次取为p1,p2的单位化向量,即
由教材中的定理5.8,q3与p1,p2正交,于是q3可取为方程
的单位解向量.由
可知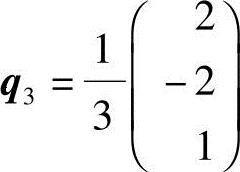 .于是
.于是
20.在某国,每年有比例为p的农村居民移居城镇,有比例为q的城镇居民移居农村,假设该国总人口数不变,且上述人口迁移的规律也不变.把n年后农村人口和城镇人口占总人口的比例依次记为xn和yn(xn+yn=1).
(1)求关系式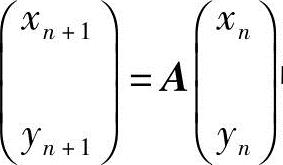 中的矩阵A;
中的矩阵A;
(2)设目前农村人口与城镇人口相等,即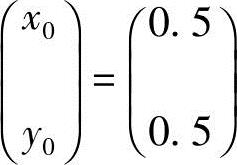 ,求
,求 .
.
解 (1)由题设,有 ,,
,,
用矩阵表示为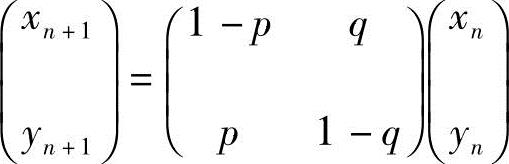 ,故
,故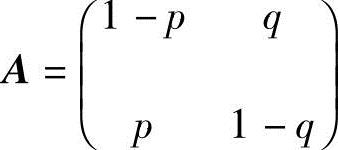 .
.
(2)由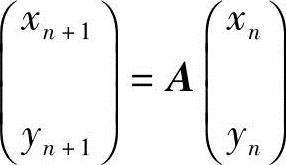 可知
可知 ,即该问题归结为求An.
,即该问题归结为求An.
由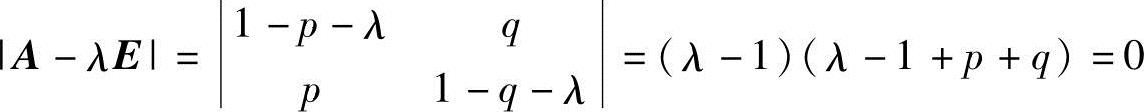 ,得A的特征值为λ1=1,λ2=1-p-q.(https://www.xing528.com)
,得A的特征值为λ1=1,λ2=1-p-q.(https://www.xing528.com)
对应于特征值λ1=1的特征向量为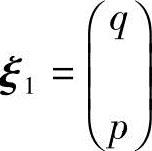 ;
;
对应于特征值λ2=1-p-q的特征向量为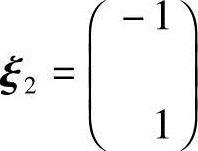 .
.
令 ,则P可逆,且
,则P可逆,且 ,其中,r=1-p-q.因此
,其中,r=1-p-q.因此
故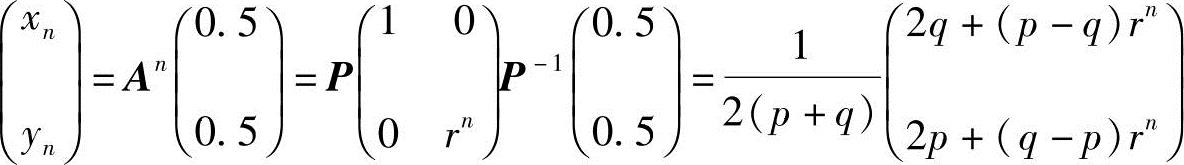 ,其中,r=1-p-q.
,其中,r=1-p-q.
21.(劳动力就业转移)某城市共有30万人从事农、工、商各行业的工作,假定这个总人数在若干年内保持不变,而社会调查表明:
(1)在这30万就业人员中,目前约有15万人从事农业,9万人从事工业,而6万人经商.
(2)在从事农业的人员中,每年约有20%改为从事工业,10%改为经商.
(3)在从事工业的人员中,每年约有20%改为从事农业,10%改为经商.
(4)在经商的人员中,每年约有10%改为从事农业,10%改为从事工业.
预测一两年后从事各行业人员的人数,以及经过多年之后,从事各行业人员总数的发展趋势.
解 若用三维向量xn表示第n年后从事这三种职业的人员总数(单位:万人),则由题
设 ,xn=Axn-1,其中,
,xn=Axn-1,其中, .因此
.因此
要求经过多年之后从事各行业人员总数的发展趋势,首先求An.
于是A的特征值为λ1=1,λ2=0.7,λ3=0.5.
对应特征值λ1=1,解方程(A-E)x=0.由
得特征向量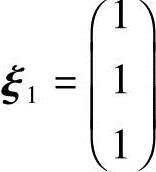 ,单位化得
,单位化得 ;
;
对应特征值λ2=0.7,解方程(A-0.7E)x=0.由
得特征向量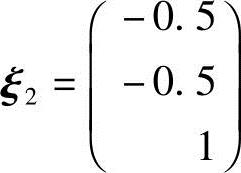 ,单位化得
,单位化得 ;
;
对应特征值λ3=0.5,解方程(A-0.5E)x=0.由
得特征向量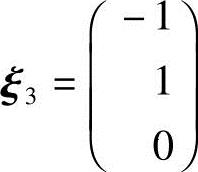 ,单位化得
,单位化得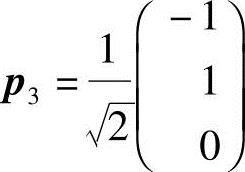 .
.
令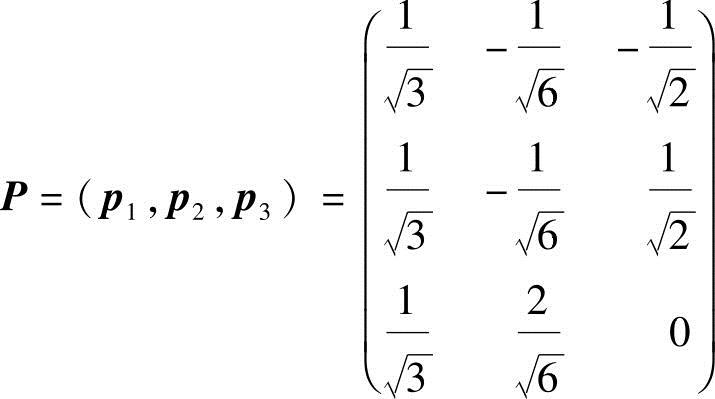 ,则P是正交阵,由A是对称阵得PTAP=
,则P是正交阵,由A是对称阵得PTAP= ,因此
,因此 ,从而
,从而
当n→∞时,
22.(1)设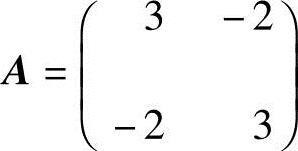 ,求φ(A)=A10-5A9;
,求φ(A)=A10-5A9;
(2)设 ,求φ(A)=A10-6A9+5A8.
,求φ(A)=A10-6A9+5A8.
解 因为A是对称矩阵,故正交相似于对角阵.
(1)由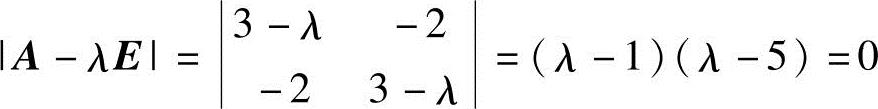 ,得A的特征值为λ1=1,λ2=5.
,得A的特征值为λ1=1,λ2=5.
对应特征值λ1=1,解方程(A-E)x=0得单位特征向量为 ;
;
对应特征值λ2=5,解方程(A-5E)x=0得单位特征向量为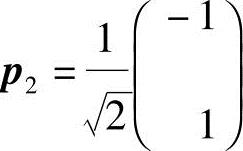 .
.
令 ,则P是正交阵,且有
,则P是正交阵,且有
其中,φ(x)=x10-5x9,φ(1)=-4,φ(5)=0.
于是A的特征值为λ1=-1,λ2=1,λ3=5.
因为A是对称阵,故存在正交矩阵Q=(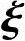 1,
1,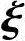 2,
2,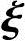 3),使
3),使
故A=QΛQT,且Q的列向量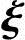 i是对应特征值λi的单位特征向量(i=1,2,3).从而
i是对应特征值λi的单位特征向量(i=1,2,3).从而
其中,φ(x)=x10-6x9+5x8,φ(-1)=12,φ(1)=0,φ(5)=0.这样,只需计算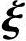 1,即对应特征值λ1=-1的单位特征向量,代入上式得φ(A).
1,即对应特征值λ1=-1的单位特征向量,代入上式得φ(A).
解方程(A+E)x=0,由
得特征向量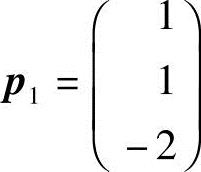 ,单位化得
,单位化得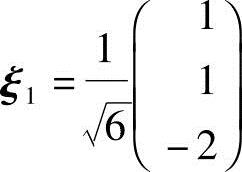 ,故
,故
23.用矩阵记号表示下列二次型:
(1)f=x2+4xy+4y2+2xz+z2+4yz;
(2)f=x2+y2-7z2-2xy-4xz-4yz;
(3)f=x21+x22+x23+x24-2x1x2+4x1x3-2x1x4+6x2x3-4x2x4.
解 (1)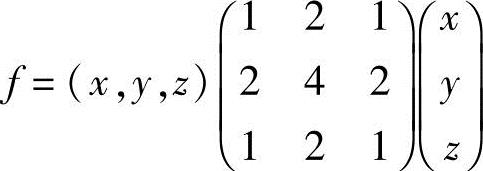 ;
;
(2) ;
;
(3) .
.
24.求一个正交变换把下列二次型化成标准形:
(1)f=2x21+3x22+3x23+4x2x3;
(2)f=x21+x23+2x1x2-2x2x3.
解 (1)二次型f的矩阵为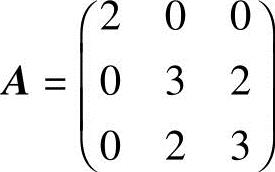 ,它的特征多项式为
,它的特征多项式为
所以A的特征值为λ1=1,λ2=2,λ3=5.
对应特征值λ1=1,解方程(A-E)x=0,由
得特征向量 ,单位化得
,单位化得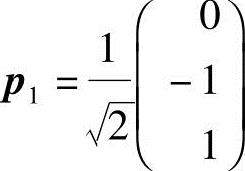 ;
;
对应特征值λ2=2,解方程(A-2E)x=0,由
得单位特征向量 ;
;
对应特征值λ3=5,解方程(A-5E)x=0,由
得特征向量 ,单位化得p
,单位化得p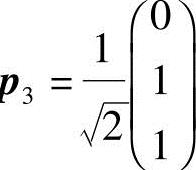 .
.
令P=(p1,p2,p3),则P是正交阵,作正交变换x=Py,即
便把f化为标准形f=y21+2y22+5y23.
(2)二次型f的矩阵为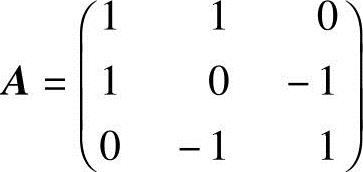 ,它的特征多项式为
,它的特征多项式为
所以A的特征值为λ1=2,λ2=1,λ3=-1.
对应特征值λ1=2,解方程(A-2E)x=0,由
得特征向量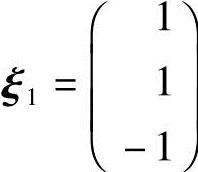 ,单位化得
,单位化得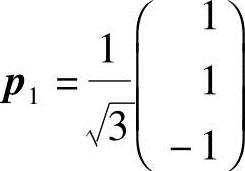 ;
;
对应特征值λ2=1,解方程(A-E)x=0,由
得特征向量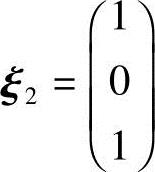 ,单位化得
,单位化得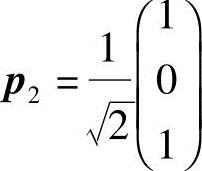 ;
;
对应特征值λ3=-1,解方程(A+E)x=0,由
得特征向量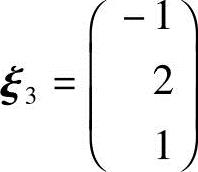 ,单位化得
,单位化得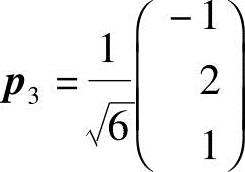 .
.
令P=(p1,p2,p3),则P是正交阵,作正交变换x=Py,即
便把f化为标准形f=2y21+y22-y23.
25.求一个正交变换把二次曲面的方程
3x2+5y2+5z2+4xy-4xz-10yz=1
化成标准方程,并指出该方程表示什么曲面?
解 记二次曲面为f=1,则f为二次型,它的矩阵为
所以A的特征值为λ1=0,λ2=2,λ3=11.
对应特征值λ1=0,解方程Ax=0,由
得特征向量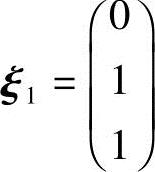 ,单位化得
,单位化得 ;
;
对应特征值λ2=2,解方程(A-2E)x=0,由
得特征向量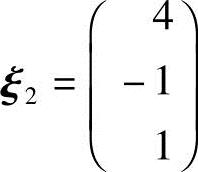 ,单位化得
,单位化得 ;
;
对应特征值λ3=11,解方程(A-11E)x=0,由
得特征向量 ,单位化得
,单位化得 .
.
令P=(p1,p2,p3),则P是正交阵,作正交变换x=Py,即
在此变换下,二次曲面的方程化为标准方程2v2+11w2=1,它表示椭圆柱面.
26.证明:二次型f=xTAx在x=1时的最大值为矩阵A的最大特征值.
证 设λ1≥λ2≥…≥λn为A的n个特征值,因为A是对称阵,故有正交变换x=Qy,使
f(x)=yTQTAQy=yTΛy=λ1y21+λ2y22+…+λny2n.
又x2=xTx=yTQTQy=yTy=y2,
从而
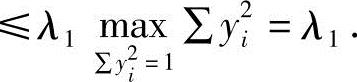
另一方面,取y0=e1=(1,0,…,0)T,即y0是第1个分量为1的单位坐标向量,再令x0=Qy0,则‖x0‖=‖y0‖=1,且二次型f在x0处的值为
f(x0)=yT1Λy0=λ1.
综合以上知maxf(x)=λ1.
‖x‖=1
27.用配方法化下列二次型成标准形,并写出所用变换的矩阵:
(1)f(x1,x2,x3)=x21+3x22+5x23+2x1x2-4x1x3;
(2)f(x1,x2,x3)=x1x2+x1x3-3x2x3.
解 (1)由于f中含变量x1的平方项,故把含x1的项归并起来,配方可得
f=x21+2x1x2-4x1x3+3x22+5x23
=(x1+x2-2x3)2-x22-4x23+4x2x3+3x22+5x23
=(x1+x2-2x3)2+2x22+4x2x3+x23,
再对后面含有x2的项配方,可得
f=(x1+x2-2x3)2+2(x2+x3)2-x23.
令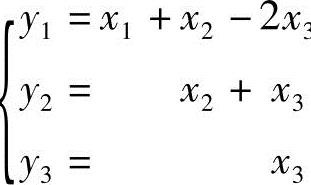 ,,即,
,,即, ,,,
,,,
写成矩阵形式:x=Cy,这里 .在此可逆变换下,就把f化成标准形f=y21+2y22-y23.
.在此可逆变换下,就把f化成标准形f=y21+2y22-y23.
(2)在f中不含有平方项,由于含有交叉项x1x2,故可先作可逆线性变换
代入可得f=y21-2y1y3-y22+4y2y3,再配方,得f=(y1-y3)2-(y2-2y3)2+3y23.
令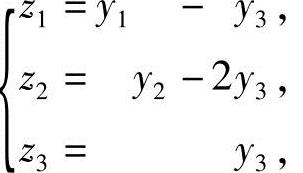 即
即 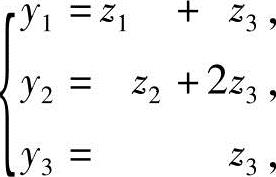
就把f化成标准形f=z21-z22+3z23.所用变换为x=Cz,其中
28.设f=x21+x22+5x23+2ax1x2-2x1x3+4x2x3为正定二次型,求a.
解 二次型f的矩阵为
由赫尔维茨定理(教材中的定理5.13),A正定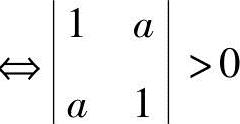 且A>0.
且A>0.
由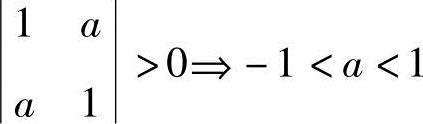 ;
;
由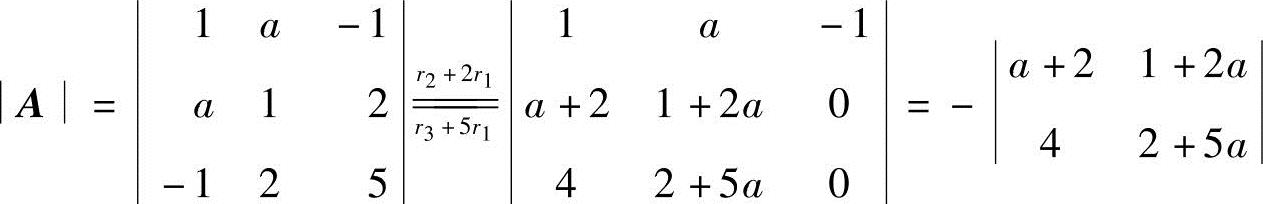
 综上可知,当
综上可知,当 时,A正定,从而f正定.
时,A正定,从而f正定.
29.判别下列二次型的正定性:
(1)f=-2x21-6x22-4x23+2x1x2+2x1x3;
(2)f=x21+3x22+9x23-2x1x2+4x1x3.
解 (1)f的矩阵为 ,它的一阶主子式a11=-2<0;2阶主子式
,它的一阶主子式a11=-2<0;2阶主子式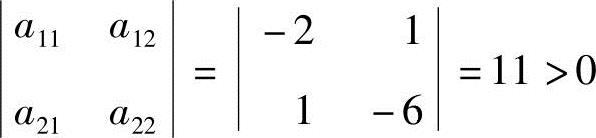 ;3阶主子式,即A=-38<0.根据赫尔维茨定理知f为负定二次型.
;3阶主子式,即A=-38<0.根据赫尔维茨定理知f为负定二次型.
(2)f的矩阵为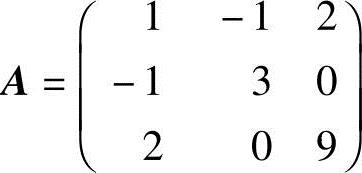 ,它的一阶主子式a11=1>0;2阶主子式
,它的一阶主子式a11=1>0;2阶主子式
 ;3阶主子式,即A=6>0.根据赫尔维茨定理知f为正定二次型.
;3阶主子式,即A=6>0.根据赫尔维茨定理知f为正定二次型.
30.证明对称阵A为正定的充分必要条件是:存在可逆矩阵U,使A=UTU,即A与单位阵E合同.
证 充分性:若存在可逆矩阵U,使A=UTU,任取x∈Rn,x≠0,就有Ux≠0,且A的二次型在该处的值
f(x)=xTAx=xTUTUx=[Ux,Ux]=Ux2>0,
即矩阵A的二次型是正定的,从而A是正定矩阵.
必要性:因为A是对称矩阵,故必存在正交阵Q,使
QTAQ=Λ=diag(λ1,λ2,…,λn),
其中,λ1,λ2,…,λn是A的全部特征值.由A正定,知λi>0(i=1,2,…,n).记对角阵Λ1=diag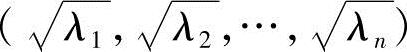 ,则有
,则有
从而
A=QΛQT=QΛ1Λ1QT=QΛ1(QΛ1)T.
记U=(QΛ1)T,显然U可逆,且由上式知A=UTU.
实验5
1.设向量组 ,将其正交规范化.
,将其正交规范化.
解 程序设计如下:
Q的前3列就是所要求的规范正交向量组.
注 设A是m×n矩阵,当m=n时,输出的变元Q是n阶正交矩阵,其列组就是待求的规范正交向量组,R是一个n阶可逆的上三角矩阵.当n<m时,输出的变元R是一个m×n行阶梯形矩阵,而Q是m阶正交矩阵,在Q中取前n列,就是待求的规范正交向量组.
2.将矩阵 对角化,但不用eig函数,而用poly,roots和null函数分步作业.
对角化,但不用eig函数,而用poly,roots和null函数分步作业.
解 在MATLAB编辑器中建立M文件如下:
运行结果为:
可逆矩阵为
对角矩阵为
3.用正交变换将二次型f=x21+x22+x23+x24+2x1x2-2x1x4-2x2x3+2x3x4化为标准形.
解 在MATLAB编辑器中建立M文件如下:
运行结果为:
正交矩阵为
对角矩阵为
标准化的二次型为
f=
-y1^2+y2^2+y3^2+3*y4^2
4.假设在一个大城市中的总人口是固定的,人口的分布则因居民在市区和郊区之间的迁徙而变化.每年有6%的市区居民搬到郊区去住,而有2%的郊区居民搬到市区.若开始时有30%的居民住在市区,70%的居民住在郊区,问10年、30年及50后市区和郊区的居民人口比例是多少?最终的变化趋势又如何?
解 这个问题可以用矩阵乘法来描述.第n年后市区和郊区的居民人口比例构成二维向量,记作xn,则
用下列MATLAB程序进行计算:
为求xn,先求A的特征值和特征向量,在MATLAB编辑器中建立M文件如下:
运行结果为:
由实验结果可以看到,将x0用A的两个线性无关的特征向量线性表示,表示式为x0=0.75p1-0.05p2,因
Ap1=p1,Ap2=0.92p2,故xn=Anx0=0.75p1-0.05·0.92np2.
显然,当n→∞时,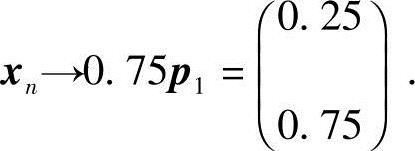
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




