线性代数学习辅导-向量空间中定义内积的意义及问题解析

问题5.1 在向量空间中定义内积有什么意义？

答 在向量空间中，向量之间的运算只定义了线性运算（加法与数乘），即加法和数乘运算.如果把三维向量空间R³与解析几何中的三维几何空间相比较，就会发现前者缺少向量的几何度量性质，如向量的长度、两向量之间的夹角等.在Rⁿ中引入向量的内积，就能合理给出向量的长度、两向量之间的夹角等定义，使之成为一个可度量的向量空间，于是进一步就有了正交向量组、单位向量、正交矩阵等概念.

问题5.2 若矩阵A与B相似，则它们有相同的特征值.反过来，若矩阵A与B有相同的特征值，那么

（1）它们是否相似？

（2）在什么条件下，它们必定相似？

答 （1）若矩阵A与B有相同的特征值，它们可能相似，也可能不相似.例如，

若取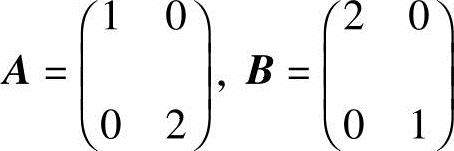，易求得两矩阵的特征值相同，均为λ₁=1，λ₂=2.将矩阵A的第1，2行及第1，2列交换可得到矩阵B，令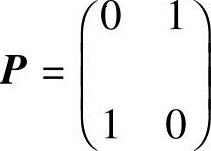，则P可逆且P^-1=P，于是P^-1AP=PAP=B，由矩阵相似的定义，知A与B相似.注：把对角阵Λ的对角元交换次序变为对角阵Λ₁，则Λ与Λ₁相似.

若取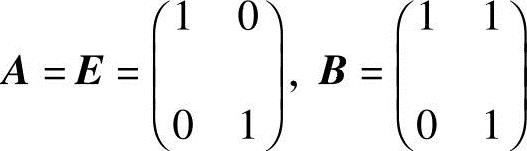，易求得两矩阵的特征值相同，均为1，但二者不相似.否则，存在2阶可逆矩阵P使得E=P^-1AP=B，与B≠E矛盾.

（2）当n阶矩阵A和B都能对角化时，若它们有相同的特征值，则它们一定相似.

事实上，设n阶矩阵A和B都能对角化且特征值相同，则A与对角阵Λ相似，B与对角阵Λ₁相似.由（1）知，Λ与Λ₁相似，从而A与B相似.

问题5.3 化二次型为标准形，为什么一定要用可逆变换？(www.xing528.com)

答 线性代数在某种意义下是研究不变性的.例如，矩阵经初等变换秩不变，对线性方程组的增广矩阵作初等行变换，所得新方程组与原方程组同解（解不变），等等.

化二次型为标准形，用可逆变换，一方面，可保证还原（变回去）；更重要的是，在形式简化的条件下，还保证变换前后两个二次型的秩和其他一些性质不变.比如实二次型还会保持各种惯性指数不变，正（负）定性不变，等等.

问题5.4 二次型的标准形是否唯一？

答 不唯一.例如，二次型f（x₁，x₂）=x₁x₂.采用配方法.

若令

在此可逆变换下，就把f化成标准形f=y²₁-y²₂. （5-1）

若令

在此可逆变换下，就把f化成标准形f=4y²₁-y²₂.（5-2）

式（5-1）和式（5-2）都是f的标准形，虽然对应的矩阵不相同，但这些矩阵却都是合同的.