1.设向量组
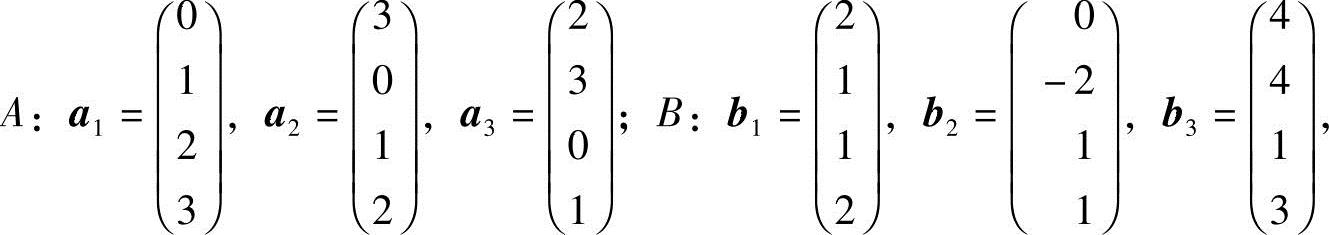
证明:B组能由A组线性表示,但A组不能由B组线性表示.
证 设A=(a1,a2,a3),B=(b1,b2,b3).利用B组能由A组线性表示⇔R(A)=R(A,B);A组不能由B组线性表示⇔R(B)<R(B,A).

可见,R(A)=R(A,B)=3,所以B组能由A组线性表示.
由矩阵(A,B)的行阶梯形,可知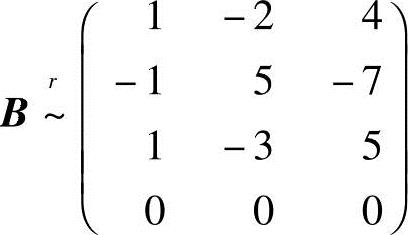 ,继续将右边的矩阵化成行阶
,继续将右边的矩阵化成行阶
梯形:
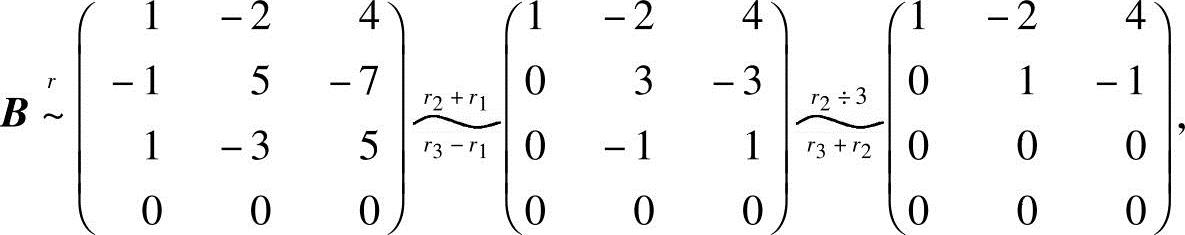
得R(B)=2<R(B,A)=3,故A组不能由B组线性表示.
注 若所作的初等行变换不同,则所得到的矩阵行阶梯形也不同.但矩阵的秩不变,它就是矩阵的行阶梯形中非零行的行数.
2.设向量组
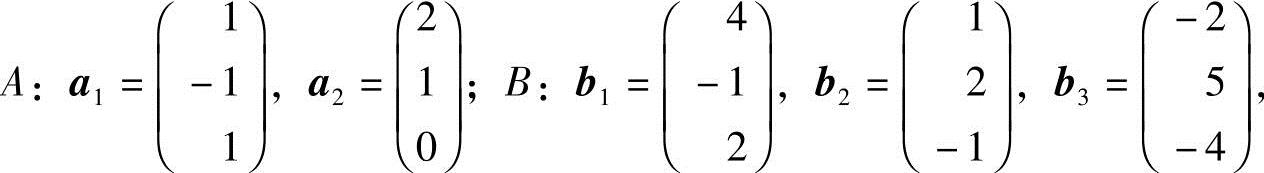
证明:A组与B组等价.
证 设A=(a1,a2),B=(b1,b2,b3),利用A组与B组等价⇔R(A)=R(A,B)=R(B).
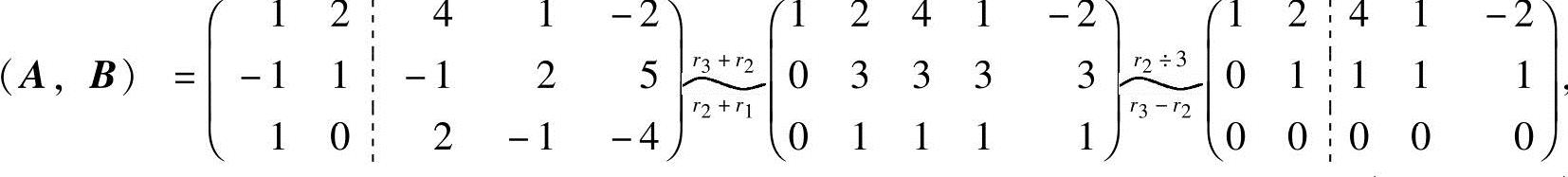
可得R(A)=R(A,B)=2.又R(B)≤R(A,B)=2,而B中有一个2阶子式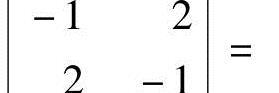 -3≠0,所以R(B)≥2,即R(B)=2,于是R(A)=R(A,B)=R(B)=2,故4组与B组等价.
-3≠0,所以R(B)≥2,即R(B)=2,于是R(A)=R(A,B)=R(B)=2,故4组与B组等价.
注 求矩阵B的秩,也可以利用矩阵的初等行变换.
3.判断下列向量组的线性相关性:
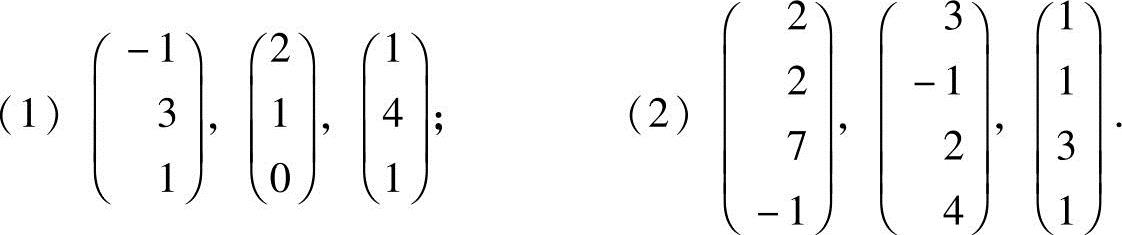
解 (1)令矩阵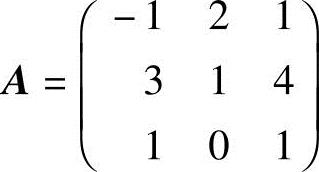 ,利用A的值是否为零,确定矩阵A的秩判断.
,利用A的值是否为零,确定矩阵A的秩判断.
因为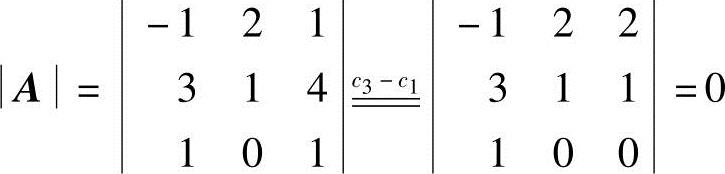 ,所以R(A)<3,故向量组(1)线性相关;
,所以R(A)<3,故向量组(1)线性相关;
(2)令矩阵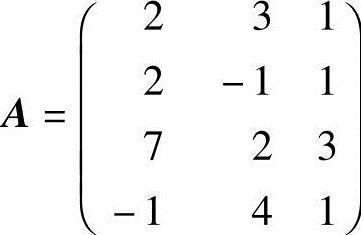 ,利用初等行变换求矩阵A的秩判断.
,利用初等行变换求矩阵A的秩判断.
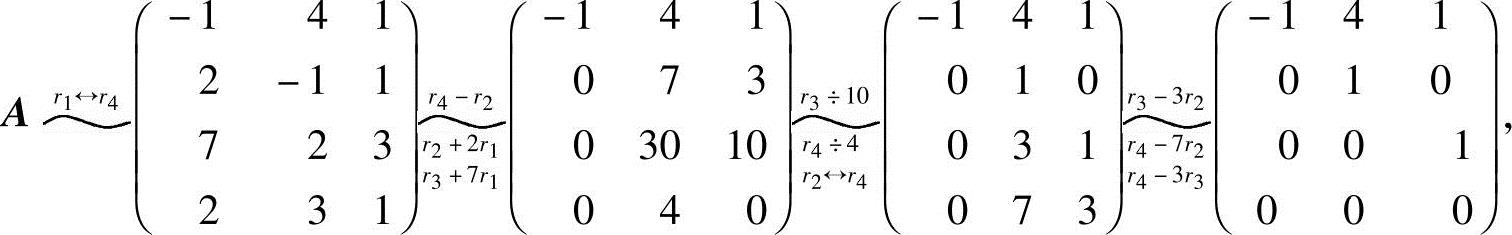
可得R(A)=3,所以向量组(2)线性无关.
4.设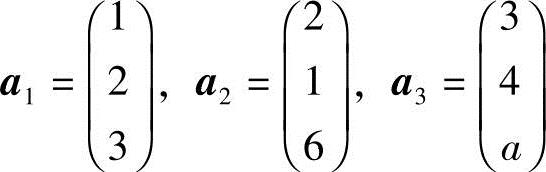 ,问a为何值时,向量组a1,a2,a3线性相关?当a为何值时,向量组a1,a2,a3线性无关?
,问a为何值时,向量组a1,a2,a3线性相关?当a为何值时,向量组a1,a2,a3线性无关?
解法一 令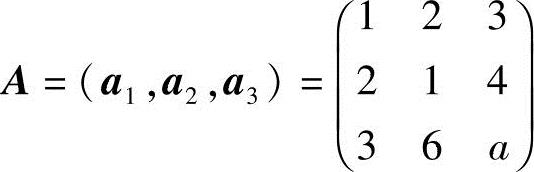 ,因为
,因为
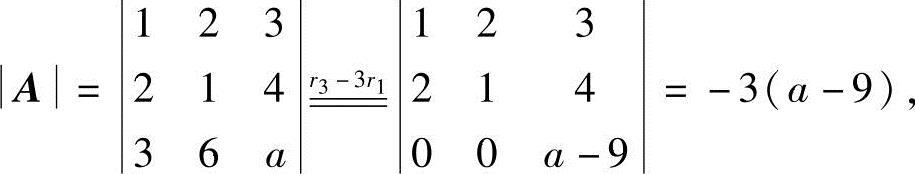
当a=9时,有A=0,得R(A)<3,所以向量组a1,a2,a3线性相关;
当a≠9时,有A≠0,得R(A)=3,所以向量组a1,a2,a3线性无关.
解法二 由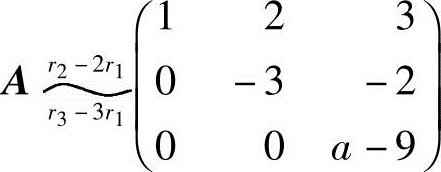 ,若向量组a1,a2,a3线性相关,则R(A)<3,得a=9;若向量组a1,a2,a3线性无关,则R(A)=3,得a≠9.
,若向量组a1,a2,a3线性相关,则R(A)<3,得a=9;若向量组a1,a2,a3线性无关,则R(A)=3,得a≠9.
5.举例说明下列命题是错误的:
(1)若向量组a1,a2,…,am线性相关,则a1可由a2,…,am线性表示.
(2)若有不全为0的数λ1,λ2,…,λm,使等式
λ1a1+λ2a2+…+λmam+λ1b1+λ2b2+…+λmbm=0成立,则a1,a2,…,am线性相关,b1,b2,…,bm也线性相关.
(3)若只有当λ1,λ2,…,λm全为0时,等式
λ1a1+λ2a2+…+λmam+λ1b1+λ2b2+…+λmbm=0才成立,则a1,a2,…,am线性无关,b1,b2,…,bm也线性无关.
(4)若a1,a2,…,am线性相关,b1,b2,…,bm也线性相关,则有不全为0的数λ1,λ2,…,λm,使等式
λ1a1+λ2a2+…+λmam=0,λ1b1+λ2b2+…+λmbm=0同时成立.
解 (1)该命题是错误的,反例:设向量组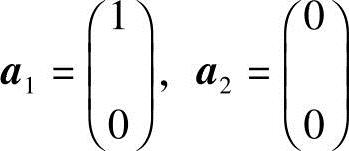 .由于向量组含零向量,所以线性相关.但a1不能由a2线性表示.
.由于向量组含零向量,所以线性相关.但a1不能由a2线性表示.
(2)该命题是错误的,反例:设向量组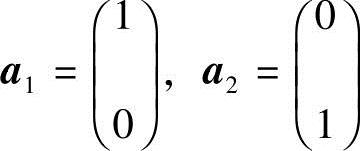 和向量组
和向量组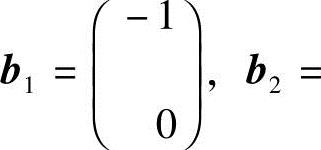
 .显然,存在不全为0的数λ1=1,λ2=1,使得等式
.显然,存在不全为0的数λ1=1,λ2=1,使得等式
λ1a1+λ2a2+λ1b1+λ2b2=0
成立.但由于a1与a2对应分量不成比例,所以向量组a1,a2线性无关.同理,向量组b1,b2也线性无关.
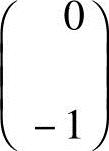
(3)该命题是错误的,反例:设向量组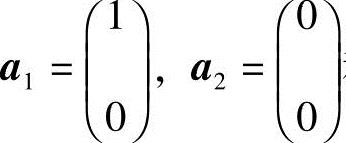 和向量组
和向量组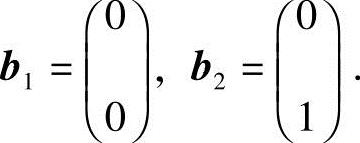 显然,若等式
显然,若等式
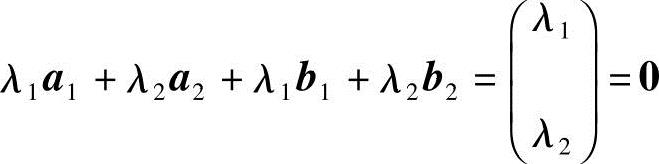
成立,当且仅当λ1=λ2=0.但向量组a1,a2线性相关,向量组b1,b2也线性相关.
注 若只有当λ1,λ2,…,λm全为0时,等式
λ1a1+λ2a2+…+λmam+λ1b1+λ2b2+…+λmbm=0
才成立,则说明向量组a1+b1,a2+b2,…,am+bm线性无关.
(4)该命题是错误的,反例:设向量组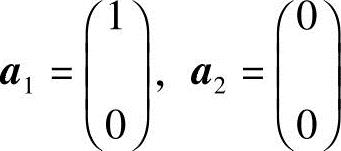 和向量组
和向量组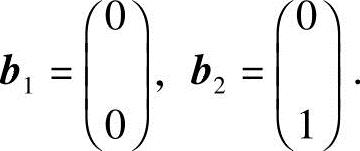 显然,向量组a1,a2线性相关,向量组b1,b2也线性相关.但若使等式
显然,向量组a1,a2线性相关,向量组b1,b2也线性相关.但若使等式
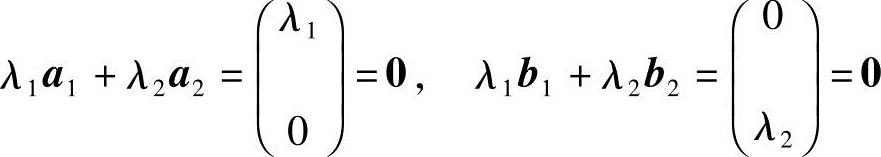
同时成立,则λ1=λ2=0.即不存在不全为0的数λ1,λ2,使得上面两个等式同时成立.
6.设b1=a1+a2,b2=a2+a3,b3=a3+a4,b4=a4+a1,证明:向量组b1,b2,b3,b4线性相关.
证法一 因为向量b4=b1-b2+b3,由向量组线性相关的等价定义,所以向量组b1,b2,b3,b4线性相关.
证法二 由已知条件,有
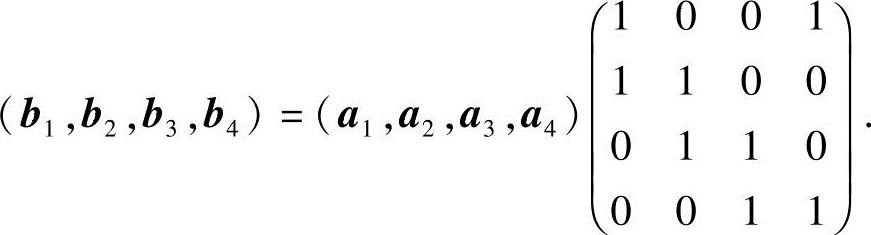
因为系数矩阵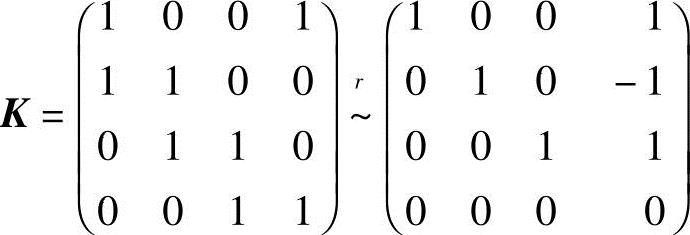 ,所以R(K)=3.
,所以R(K)=3.
又由矩阵秩的性质,有R(b1,b2,b3,b4)≤R(K)=3<4(向量的个数),故向量组b1,b2,b3,b4线性相关.
7.设b1=a1,b2=a1+a2,…,br=a1+a2+…+ar,且向量组a1,a2,…,ar线性无关,证明:向量组b1,b2,…,br也线性无关.
证法一 利用向量组线性相关性的定义.
令
x1b1+x2b2+…+xrbr=0,
即
(x1+x2+…+xr)a1+(x2+…+xr)a2+…+xrar=0
由向量组a1,a2,…,ar线性无关,有
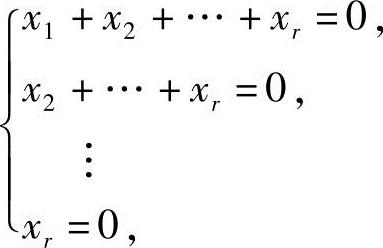
可得x1=x2=…=xr=0,所以向量组b1,b2,…,br也线性无关.
证法二 利用矩阵(b1,b2,…,br)的秩判断.由b1=a1,b2=a1+a2,…,br=a1+a2+…+ar,有
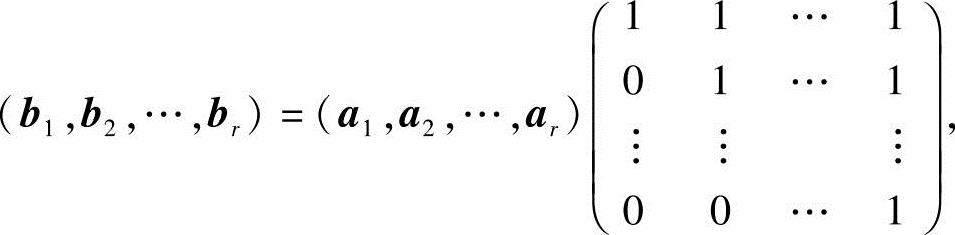
因为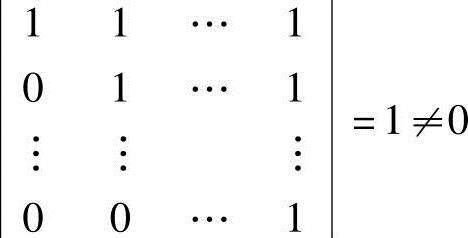 ,所以矩阵
,所以矩阵 可逆,从而有
可逆,从而有
R(b1,b2,…,br)=R(a1,a2,…,ar).
又因为向量组a1,a2,…,ar线性无关,所以R(a1,a2,…,ar)=r,于是
R(b1,b2,…,br)=r,
故向量组b1,b2,…,br也线性无关.
8.求下列向量组的秩和一个最大无关组:
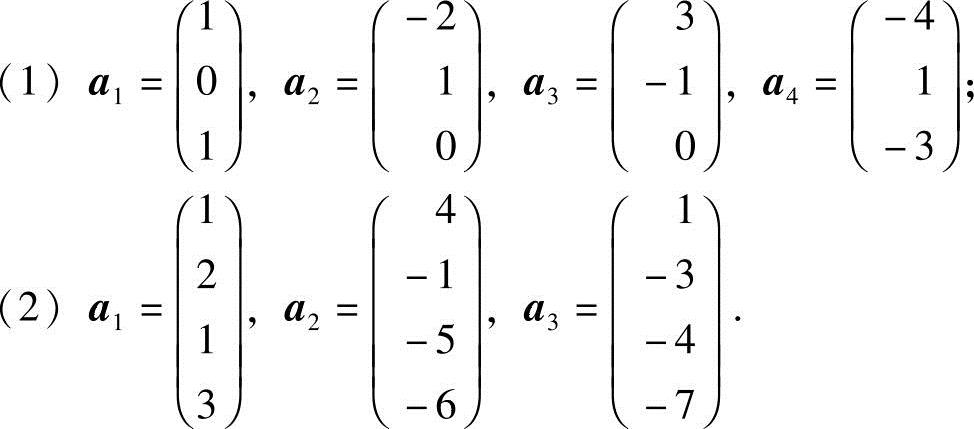
解 (1)设A=(a1,a2,a3,a4),用矩阵的初等行变换,将A化成行阶梯形:
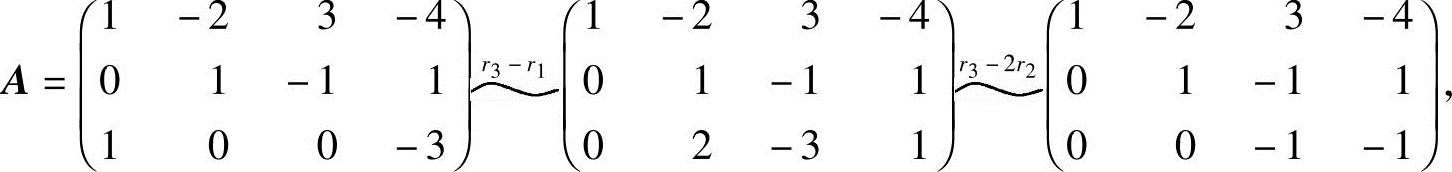
所以向量组的秩R(a1,a2,a3,a4)=3,且它的一个最大无关组为a1,a2,a3或a1,a2,a4;
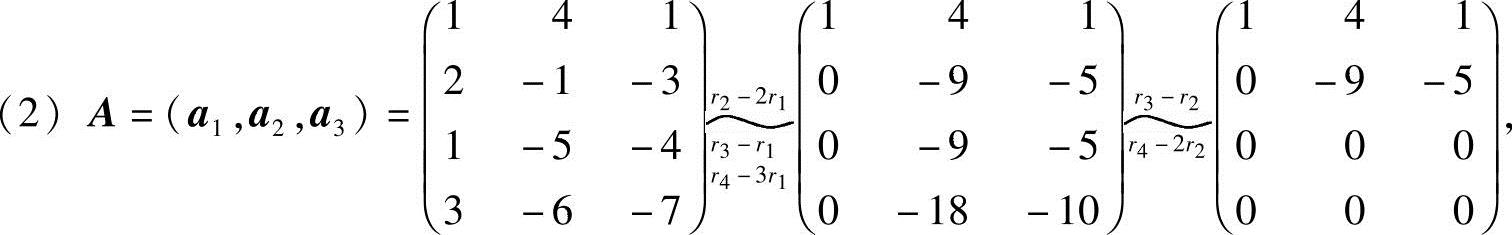
所以向量组的秩R(a1,a2,a3)=2,且它的一个最大无关组为a1,a2或a1,a3.
9.(1)设向量组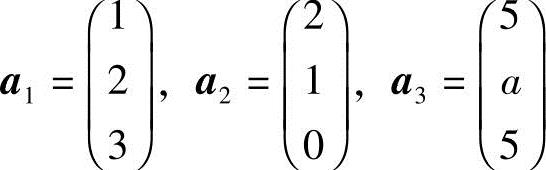 的秩为2,求a;
的秩为2,求a;
(2)设向量组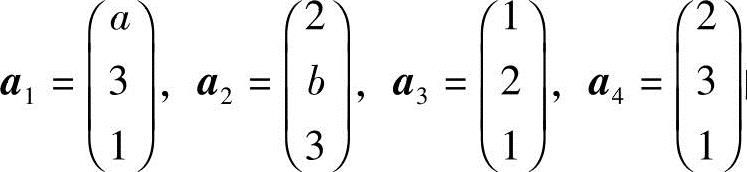 的秩为2,求a,b.
的秩为2,求a,b.
解 (1)令矩阵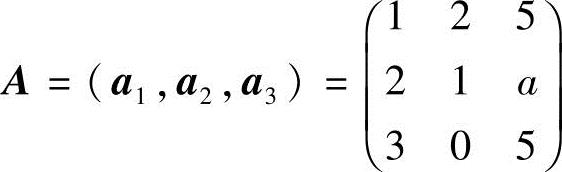 ,已知R(A)=2,有A=0.又A=
,已知R(A)=2,有A=0.又A=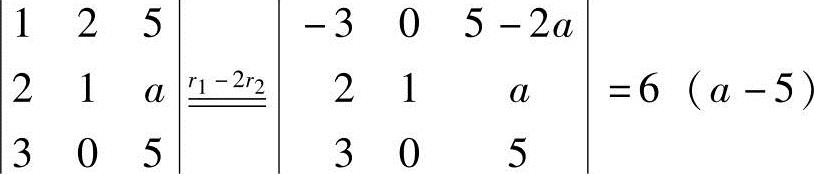 ,所以a=5;
,所以a=5;
(2)令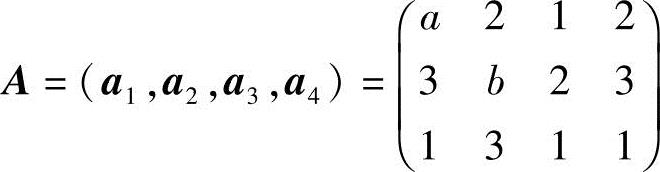 ,则
,则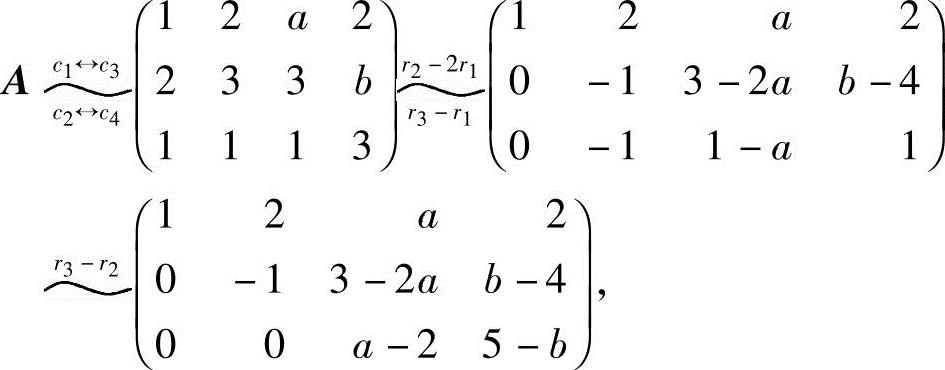
由R(A)=2,有a-2=0,5-b=0,即a=2,b=5.
10.利用矩阵的初等行变换,求下列矩阵的列向量组的一个最大无关组,并把其余列向量用最大无关组线性表示:

解 (1)令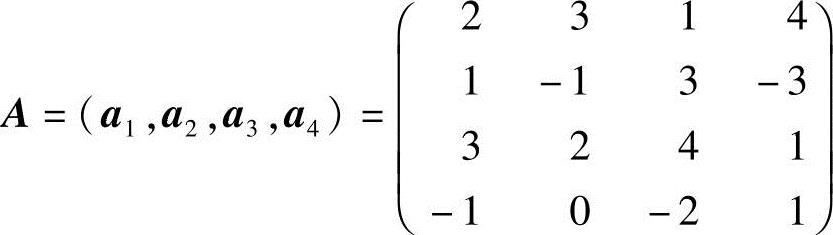 ,将A化成行最简形:
,将A化成行最简形: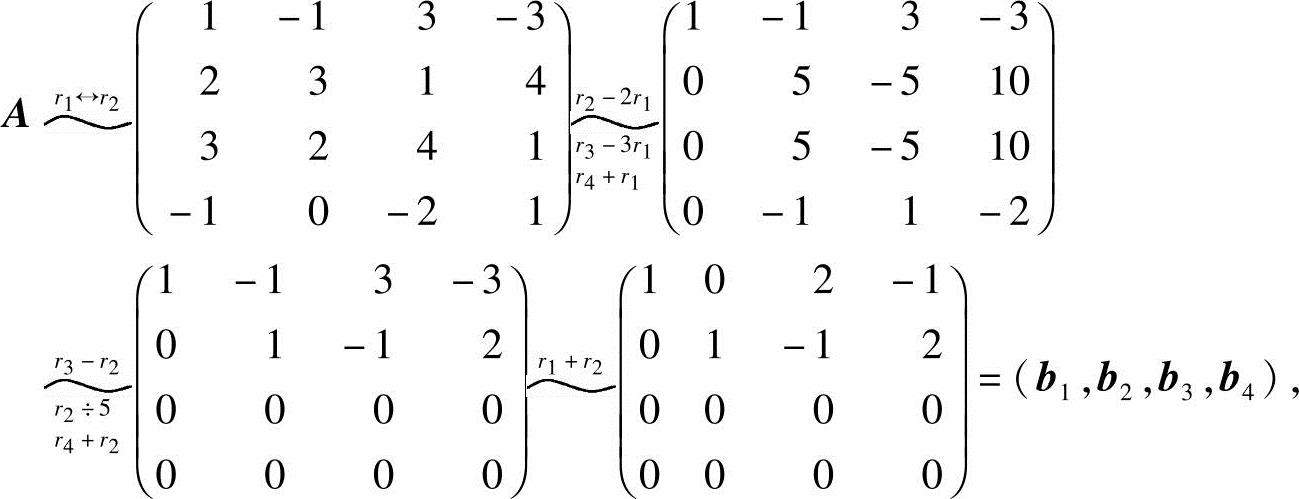
由A的行最简形,知a1,a2是A的列向量组的一个最大无关组,且有
b3=2b1-b2,b4=-b1+2b2.
因为对矩阵A作初等行变换不改变A的列向量之间的线性关系,所以由上式,可得
a3=2a1-a2,a4=-a1+2a2;
(2)令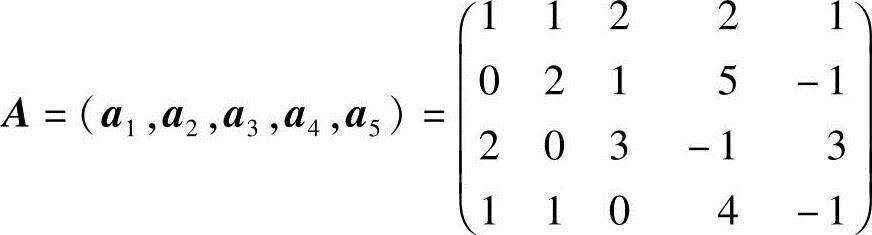 ,将A化成行最简形:
,将A化成行最简形: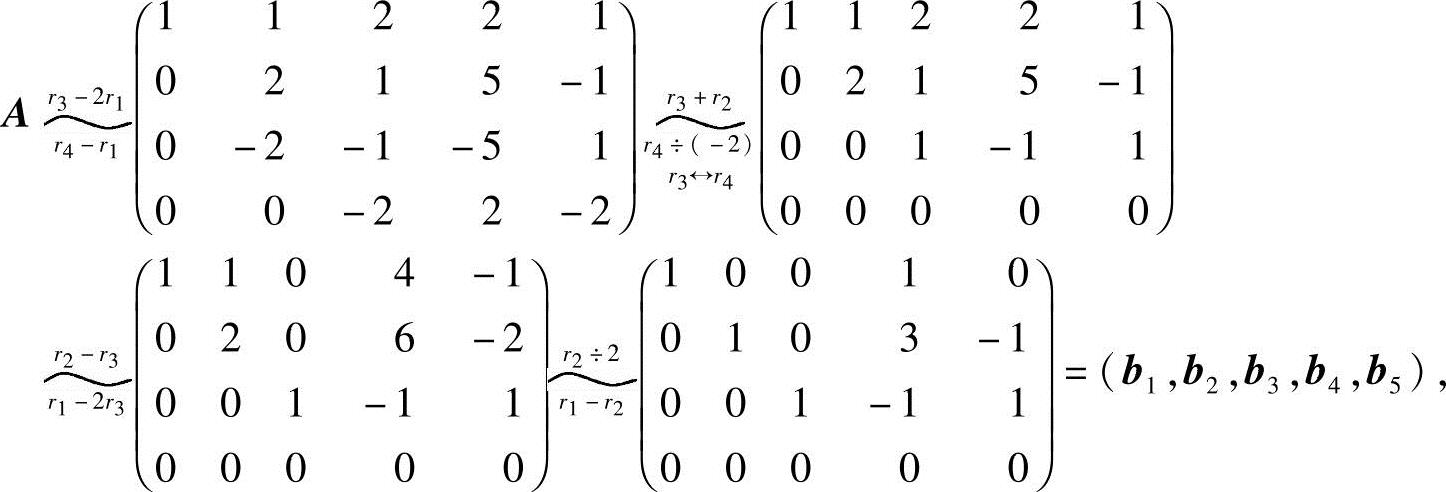
由A的行最简形,知a1,a2,a3是A的列向量组的一个最大无关组,且有
b4=b1+3b2-b3,b5=-b2+b3.
因为对矩阵A作初等行变换不改变A的列向量之间的线性关系,所以由上式,可得
a4=a1+3a2-a3,a5=-a2+a3.
11.设n维向量a1,a2,…,an,若n维单位坐标向量e1,e2,…,en能由它们线性表示,证明:a1,a2,…,an线性无关.
证 若e1,e2,…,en能由a1,a2,…,an线性表示,则有
n=R(e1,e2,…,en)≤R(a1,a2,…,an).
又R(a1,a2,…,an)≤n(向量的个数),所以R(a1,a2,…,an)=n,故向量组a1,a2,…,an线性无关.
12.设n维向量a1,a2,…,an,证明:它们线性无关的充分必要条件是任一n维向量都可由它们线性表示.
证 必要性.设向量b为任意n维向量.若a1,a2,…,an线性无关,又a1,a2,…,an,b线性相关(因为向量个数大于向量维数),则向量b一定可由向量组a1,a2,…,an线性表示.
充分性.若任一n维向量都可由a1,a2,…,an线性表示,则n维单位坐标向量e1,e2,…,en也可由它们线性表示,所以有
n=R(e1,e2,…,en)≤R(a1,a2,…,an)≤n(向量个数),即R(a1,a2,…,an)=n,所以向量组a1,a2,…,an线性无关.
13.设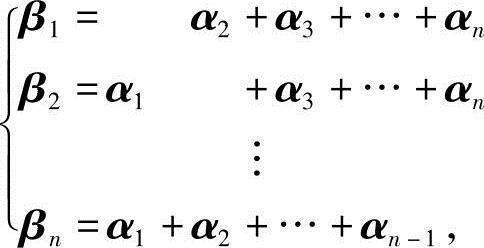 ,,证明:向量组α1,α2,…,αn与β1,β2,…,βn等价.
,,证明:向量组α1,α2,…,αn与β1,β2,…,βn等价.
证 显然,向量组β1,β2,…,βn可由向量组α1,α2,…,αn线性表示.
又
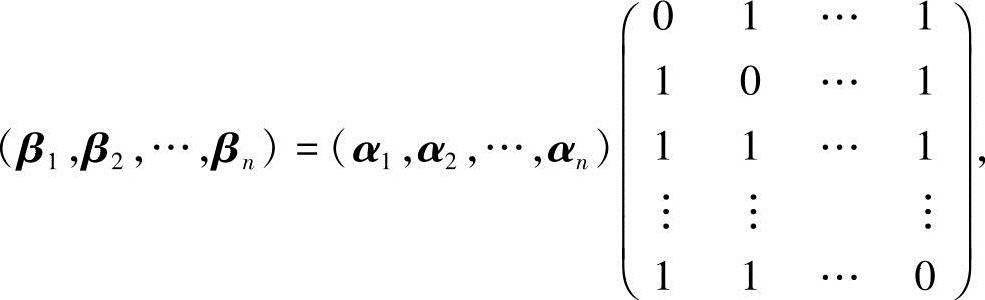
设系数矩阵为K,因为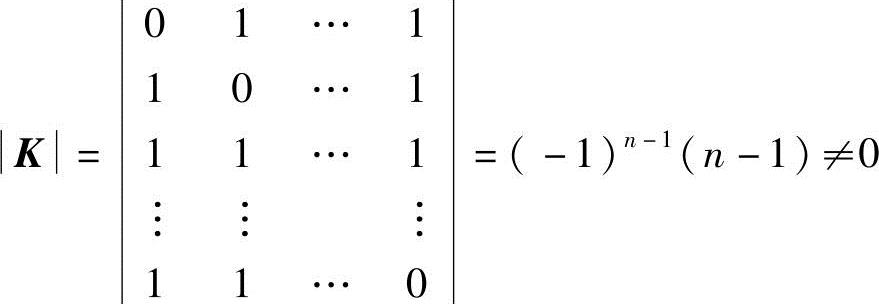 ,所以K可逆,从而
,所以K可逆,从而
(α1,α2,…,αn)=(β1,β2,…,βn)K-1,
即向量组α1,α2,…,αn又可由向量组β1,β2,…,βn线性表示,故向量组α1,α2,…,αn与向量组β1,β2,…,βn等价.
14.求下列齐次线性方程组的基础解系与通解:
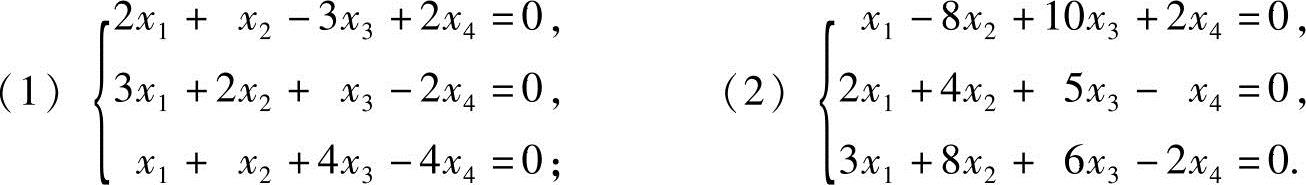
·解 (1)系数矩阵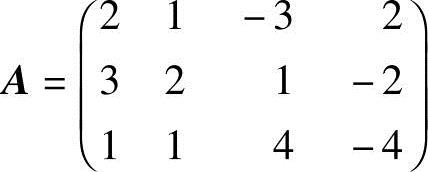 ,将A化成行最简形:
,将A化成行最简形:
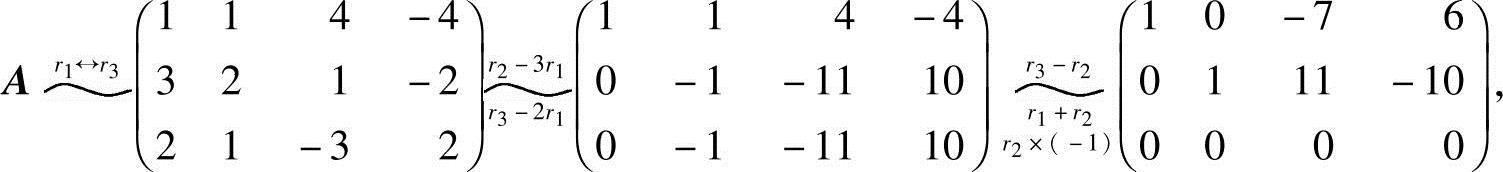
由A的行最简形,得方程组(1)的同解方程组
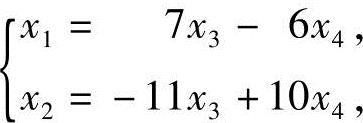
分别取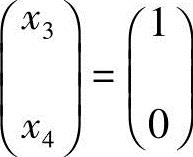 和
和 ,得
,得 ,从而方程组(1)的基础解系为
,从而方程组(1)的基础解系为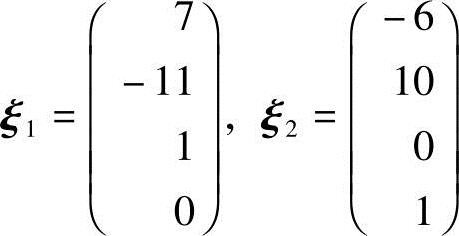 ,通解为x=c1
,通解为x=c1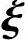 1+c2
1+c2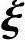 2,即
2,即
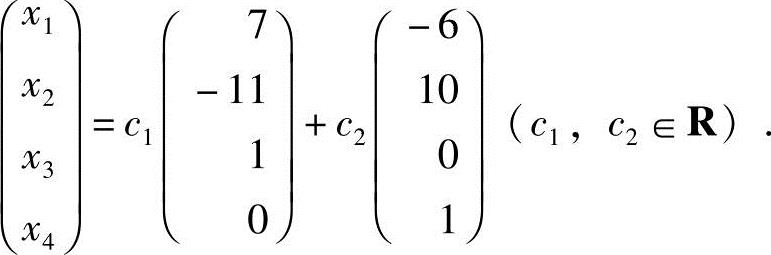
(2)解法一 系数矩阵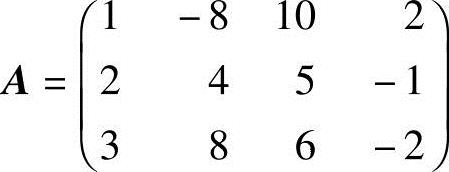 ,将A化成行最简形:
,将A化成行最简形:
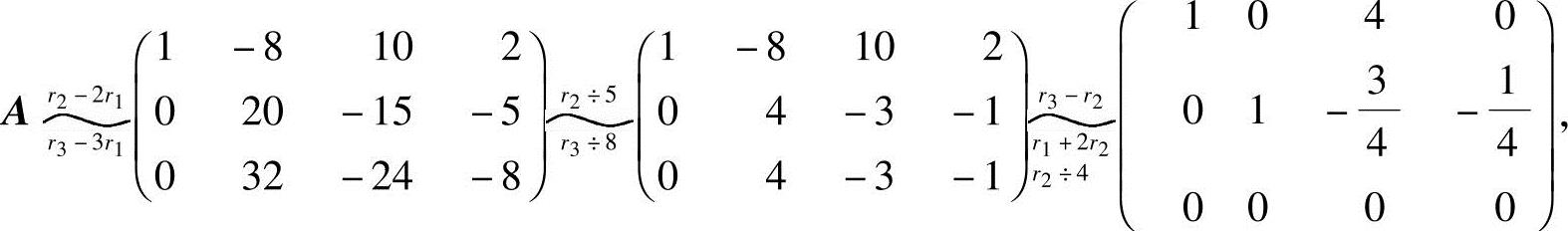
由A的行最简形,得方程组(2)的同解方程组:
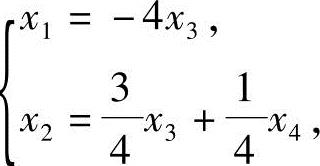
分别取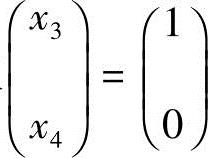 和
和 ,得
,得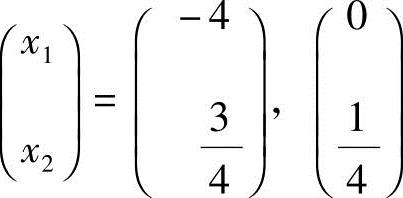 ,从而方程组(2)的基础解系为
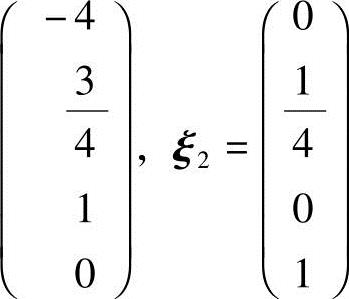
,从而方程组(2)的基础解系为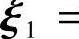
 ,通解为:x=c1
,通解为:x=c1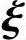 1+c2
1+c2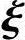 2,即
2,即
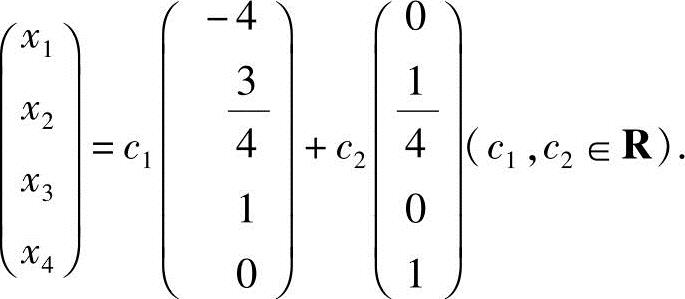
解法二 为了避免分数运算,可将系数矩阵化简为:
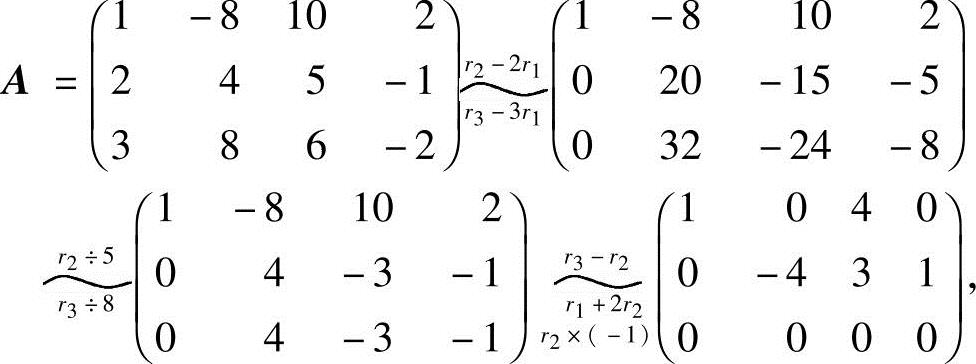
上面最后一个矩阵虽然不是A的行最简形,但与行最简形等效,这时取x1,x4为非自由的
未知数,x2,x3为自由的未知数,得方程组(2)的同解方程组
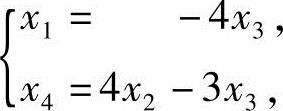
分别取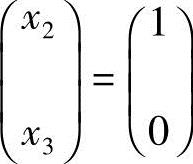 和
和 ,得
,得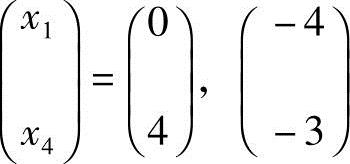 ,从而方程组(2)的基础解系为
,从而方程组(2)的基础解系为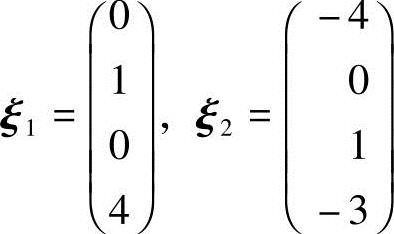 ,通解为x=c1
,通解为x=c1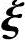 1+c2
1+c2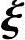 2,即
2,即
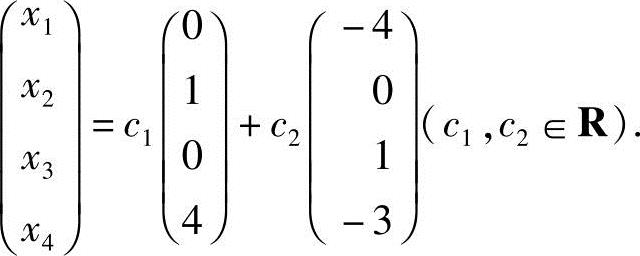
注 方程组的基础解系往往不唯一,所以由它表示的通解形式也不唯一.
15.设矩阵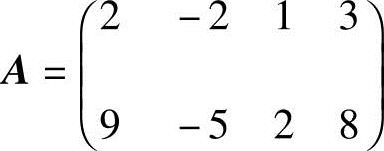 ,求一个4×2矩阵B,使AB=O,且R(B)=2.
,求一个4×2矩阵B,使AB=O,且R(B)=2.
解 因为B是4×2矩阵,且满足AB=O,令B=(b1,b2),则Abi=0(i=1,2),即B的列向量b1,b2是齐次线性方程组Ax=0的解向量.又R(B)=2,则B的列向量b1,b2线性无关,从而b1,b2是方程组Ax=0线性无关的解向量.
又A是2×4矩阵,且A的两个行向量对应分量不成比例,所以R(A)=2,所以b1,b2就是四元齐次线性方程组Ax=0的一个基础解系.
为了避免分数运算,可以按下面的方法化简系数矩阵:
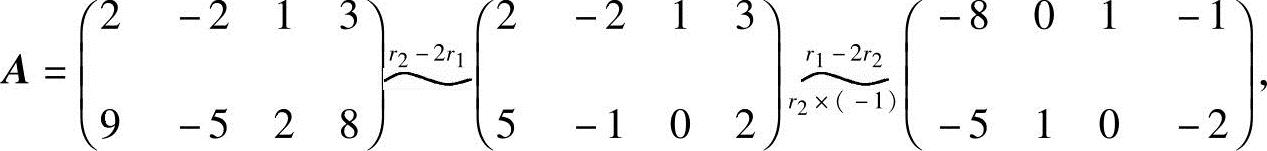
最后一个矩阵虽然不是A的行最简形,但效果等同.由此,得同解方程组
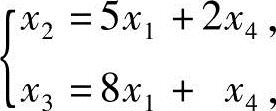
分别取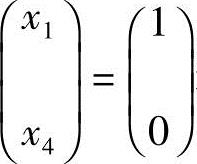 和
和 ,得
,得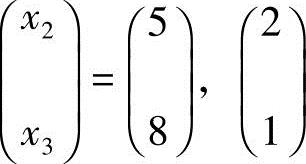 ,从而方程组Ax=0的基础解系为
,从而方程组Ax=0的基础解系为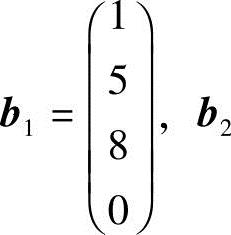
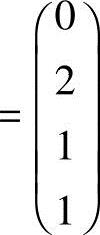 ,故矩阵
,故矩阵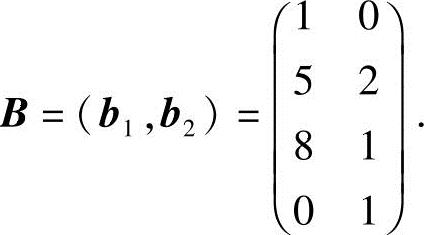
注 因为方程组Ax=0的基础解系不唯一,所以所求的矩阵B也不唯一.
16.设A为n阶矩阵(n≥2),A*为A的伴随阵,证明:
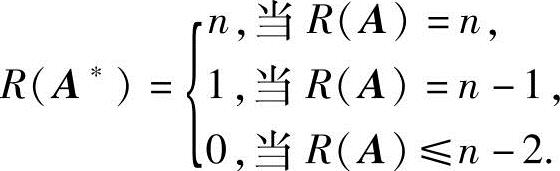
证 当R(A)=n时,有A≠0.又A*=An-1≠0,所以R(A*)=n.
当R(A)=n-1时,有A=0.又AA*=AE=O,由矩阵秩的性质,有R(A)+R(A*)≤n,从而R(A*)≤n-R(A)=n-(n-1)=1.
又由矩阵秩的定义,当R(A)=n-1时,矩阵A中必有一个n-1阶子式不为零,而由伴随阵A*的构成,知A*中必有一个元素不为零,从而R(A*)≥1.所以,当R(A)=n-1时,有R(A*)=1.
当R(A)≤n-2时,由矩阵秩的定义,矩阵A中所有n-1阶子式都为零,又由伴随阵A*的构成,知A*=O,所以R(A*)=0.(https://www.xing528.com)
17.求解下列非齐次线性方程组:
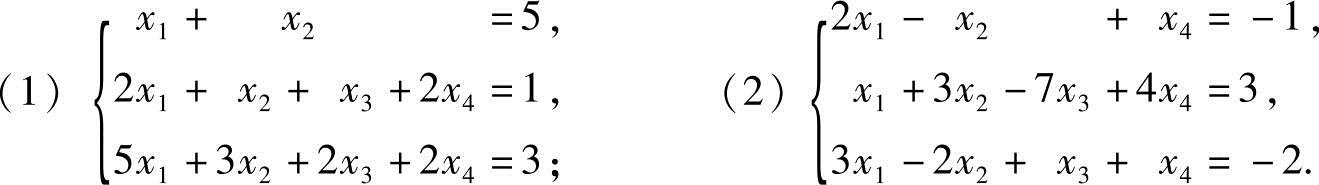
解 (1)先将方程组的增广矩阵化成行阶梯形:
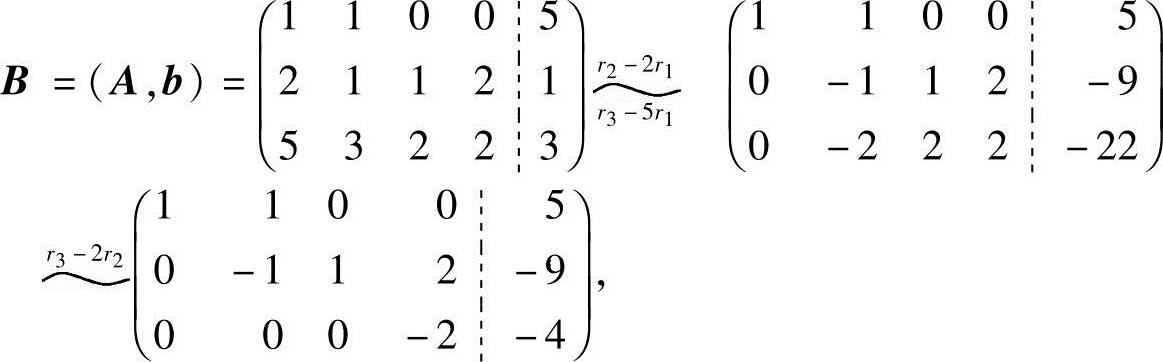
可得R(A)=R(B)=3<4,方程组(1)有无穷多解.
将B的行阶梯形矩阵进一步化成行最简形:
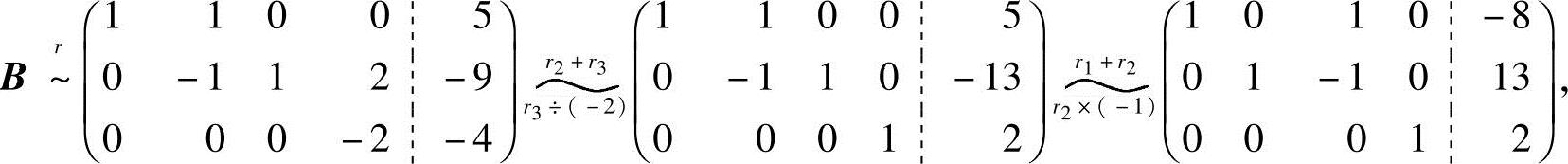
由B的行最简形,得同解方程组:
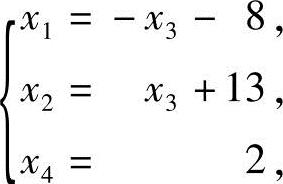
令x3=0,得方程组(1)的一个特解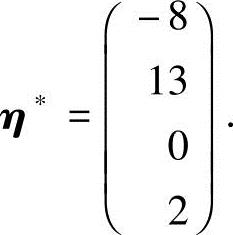
方程组(1)对应的齐次线性方程组的同解方程组为
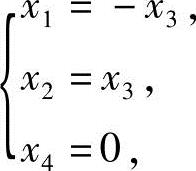
令x3=1,得齐次线性方程组的基础解系: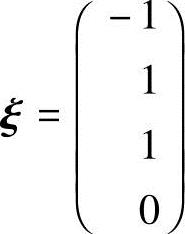 ,所以方程组(1)的通解为x=c
,所以方程组(1)的通解为x=c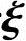 +η*,即
+η*,即
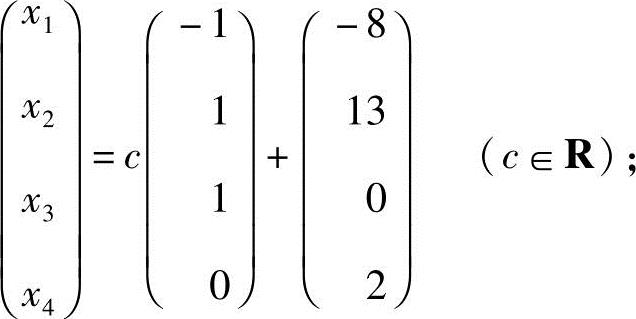
(2)先将方程组的增广矩阵化成行阶梯形:

可得R(A)=R(B)=2<4,方程组(2)有无穷多解.
将B的行阶梯形矩阵进一步化成行最简形
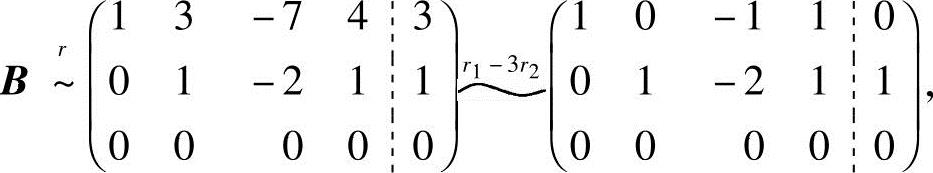
由B的行最简形,得同解方程组
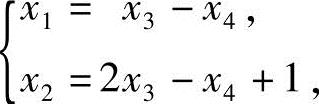
令x3=x4=0,得方程组(2)的一个特解η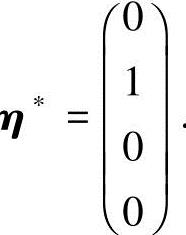
方程组(2)对应的齐次线性方程组的同解方程组
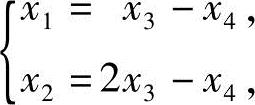
分别取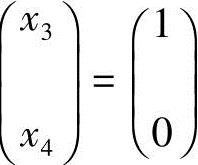 和
和 ,得
,得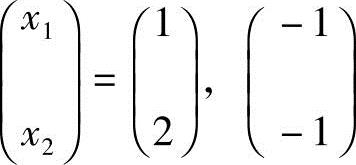 ,得齐次线性方程组的基础解系
,得齐次线性方程组的基础解系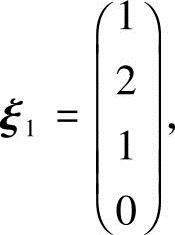
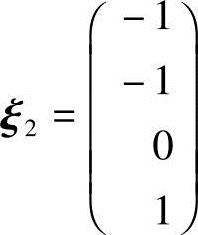 ,所以方程组(2)的通解为x=c1
,所以方程组(2)的通解为x=c1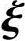 1+c2
1+c2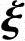 2+η*,即
2+η*,即
注 本题是按非齐次线性方程组通解的结构求解的,但也可以按第3章介绍过的方法求解.
18.设四元非齐次线性方程组的系数矩阵的秩为3,已知η1,η2,η3是它的3个解向量,且
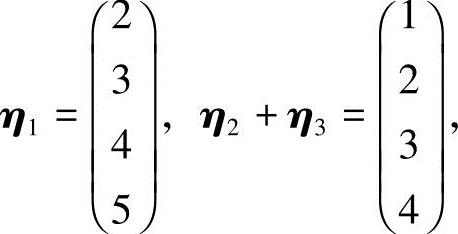
求该方程组的通解.
解 设四元非齐次线性方程组为Ax=b,对应的齐次线性方程组为Ax=0.由R(A)=3,知方程组Ax=0的基础解系只含有一个解向量,且它的任一非零解向量都可以作为它的基础解系.
已知η1,η2,η3是Ax=b的解向量,由方程组Ax=b与Ax=0解向量之间的关系,可得η1-η2,η1-η3是方程组Ax=0的解向量,从而(η1-η2)+(η1-η3)也是方程组Ax=0
的解向量,且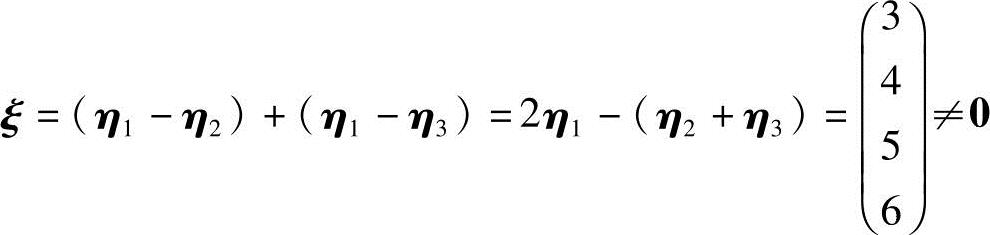 ,所以
,所以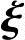 是方程组Ax=0的基础解系.
是方程组Ax=0的基础解系.
由非齐次线性方程组通解的结构,方程组Ax=b的通解为x=c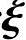 +η1,即
+η1,即
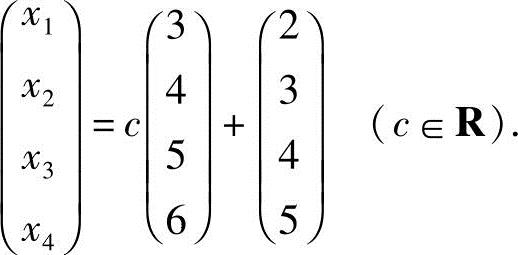
19.设矩阵A=(a1,a2,a3,a4),其中a2,a3,a4线性无关,a1=2a2-a3.向量b=a1+a2+a3+a4,求非齐次线性方程组Ax=b的通解.
解 因为矩阵A含有4个列向量,所以Ax=b为四元线性方程组.又A的列向量a2,a3,a4线性无关,而a1=2a2-a3,说明a1,a2,a3,a4线性相关,因而R(A)=3,所以方程组Ax=b对应的齐次线性方程组Ax=0的基础解系只含有一个解向量.又a1=2a2-a3,得a1-2a2+a3=0,即
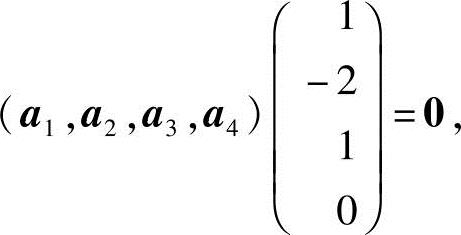
所以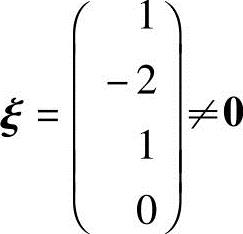 就是齐次线性方程组Ax=0的基础解系.又向量b=a1+a2+a3+a4,即(a1,a2,a3,a4)
就是齐次线性方程组Ax=0的基础解系.又向量b=a1+a2+a3+a4,即(a1,a2,a3,a4)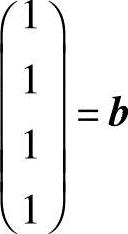 ,所以
,所以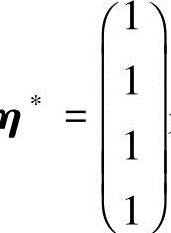 是非齐次线性方程组Ax=b的一个特解.
是非齐次线性方程组Ax=b的一个特解.
因此,方程组Ax=b的通解为x=c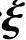 +η*,即
+η*,即
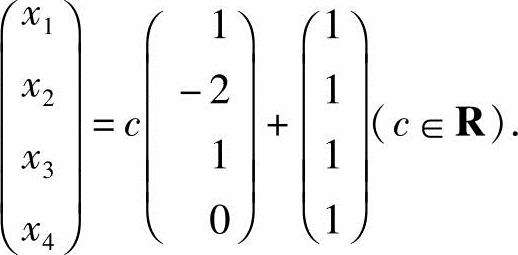
20.设向量组A: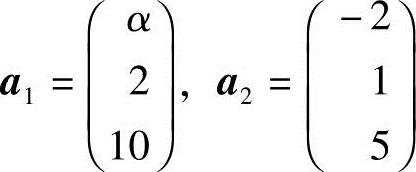 ,
,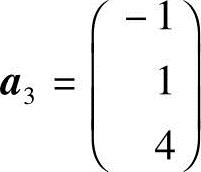 ,向量
,向量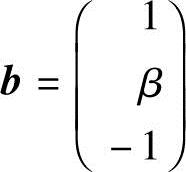 ,问α,β为何值时,(1)向量b不能由向量组A线性表示;(2)向量b能由向量组A线性表示,且表示式唯一;(3)向量b能由向量组A线性表示,且表示式不唯一,并求一般表示式.
,问α,β为何值时,(1)向量b不能由向量组A线性表示;(2)向量b能由向量组A线性表示,且表示式唯一;(3)向量b能由向量组A线性表示,且表示式不唯一,并求一般表示式.
解 设矩阵A=(a1,a2,a3).向量b能否由向量组A线性表示等价于方程组Ax=b是否有解,本题属于含参数α,β的非齐次线性方程组Ax=b的求解问题.
本题从第(2)问入手,由于方程组的系数行列式
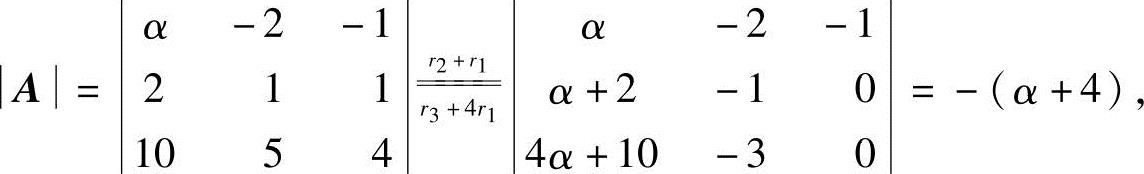
所以当A≠0,即α≠-4时,方程组Ax=b有唯一解,即向量b能由向量组A线性表示,且表示式唯一;
(1)当α=-4时,方程组的增广矩阵

当β≠0时,由于R(A)=2<R(B)=3,则方程组Ax=b无解,即向量b不能由向量组A线性表示;
(2)当α=-4,β=0时,方程组的增广矩阵
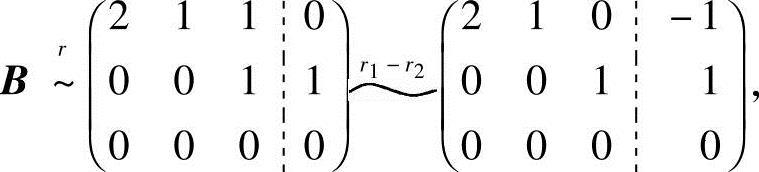
可见,R(A)=R(B)=2<3,方程组Ax=b有无穷多解,即向量b能由向量组A线性表示,且表示式不唯一.这时,方程组Ax=b的同解方程组为
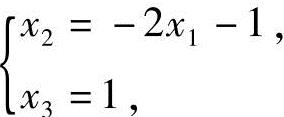
令x1=c,得方程组Ax=b的通解
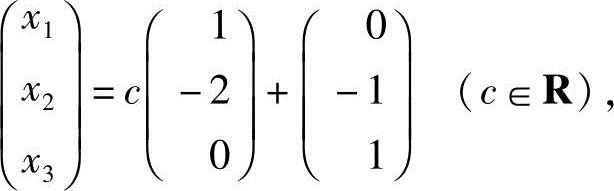
所以,向量b能由向量组A线性表示的一般式为
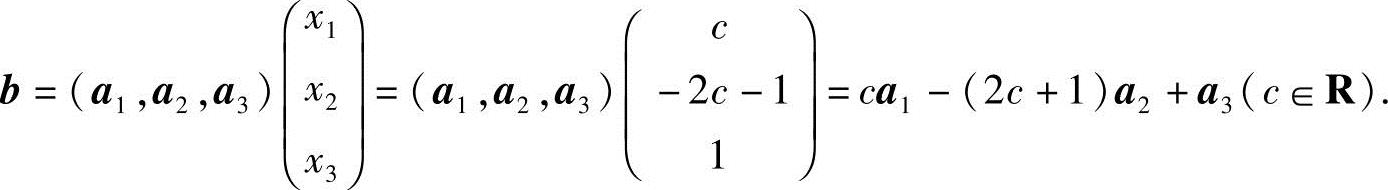
21.设η*是非齐次线性方程组Ax=b的一个解,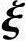 1,
1,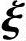 2,…,
2,…,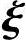 n-r是对应的齐次线性方程组Ax=0的一个基础解系,证明:
n-r是对应的齐次线性方程组Ax=0的一个基础解系,证明:
(1)η*,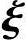 1,
1,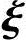 2,…,
2,…,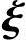 n-r线性无关;
n-r线性无关;
(2)η*,η*+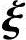 1,η*+
1,η*+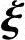 2,…,η*+
2,…,η*+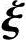 n-r线性无关.
n-r线性无关.
(1)证法一 用反证法.假设η*,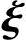 1,
1, 2,…,
2,…,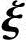 n-r线性相关.因为
n-r线性相关.因为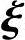 1,
1,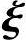 2,…,
2,…,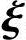 n-r是对应的齐次线性方程组Ax=0的基础解系,所以
n-r是对应的齐次线性方程组Ax=0的基础解系,所以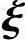 1,
1,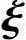 2,…,
2,…,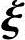 n-r线性无关.又由假设,可知η*必可由
n-r线性无关.又由假设,可知η*必可由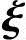 |,
|,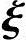 |,…,
|,…,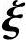 |线性表示,从而η*是对应的齐次线性方程组Ax=0的解,这与已知η*是非齐次线性方程组Ax=b的解相矛盾,故η*,
|线性表示,从而η*是对应的齐次线性方程组Ax=0的解,这与已知η*是非齐次线性方程组Ax=b的解相矛盾,故η*,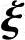 1,
1,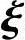 2,…,
2,…,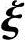 n-r线性无关;
n-r线性无关;
证法二 利用向量组线性相关性的定义.
令
x0η*+x1 1+x2
1+x2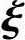 2+…+xn-r
2+…+xn-r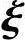 n-r=0. (4-3)
n-r=0. (4-3)
用矩阵A左乘式(4-3)两边,得
x0Aη*+x1A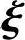 1+x2A
1+x2A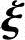 2+…+xn-rA
2+…+xn-rA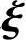 n-r=0,由
n-r=0,由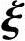 1,
1,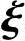 2,…,
2,…,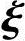 n-r是方程组Ax=0的解,η*是方程组Ax=b的解,有x0b=0,又由b≠0,得x0=0.于是式(4-3)变为
n-r是方程组Ax=0的解,η*是方程组Ax=b的解,有x0b=0,又由b≠0,得x0=0.于是式(4-3)变为
x1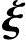 1+x2
1+x2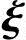 2+…+xn-r
2+…+xn-r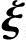 n-r=0.
n-r=0.
因为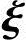 1,
1,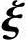 2,…,
2,…,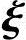 n-r是方程组Ax=0的基础解系,所以
n-r是方程组Ax=0的基础解系,所以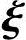 1,
1,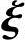 2,…,
2,…,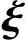 n-r线性无关,由上式,得x1=x2=…=xn-r=0,故η*,
n-r线性无关,由上式,得x1=x2=…=xn-r=0,故η*,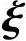 1,
1,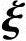 2,…,
2,…,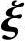 n-r线性无关;
n-r线性无关;
(2)令
x0η*+x1(η*+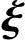 1)+x2(η*+
1)+x2(η*+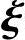 2)+…+xn-r(η*+
2)+…+xn-r(η*+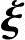 n-r)=0,即
n-r)=0,即
(x0+x1+x2+…+xn-r)η*+x1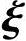 1+x2
1+x2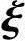 2+…+xn-r
2+…+xn-r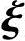 n-r=0,由(1)问的结论η*,
n-r=0,由(1)问的结论η*,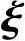 1,
1,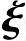 2,…,
2,…,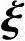 n-r线性无关,得x0=x1=…=xn-r=0,所以η*,η*+
n-r线性无关,得x0=x1=…=xn-r=0,所以η*,η*+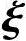 1,η*+
1,η*+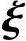 2,…,η*+
2,…,η*+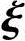 n-r线性无关.
n-r线性无关.
22.设η1,η2,…,ηs是非齐次线性方程组Ax=b的s个解,k1,k2,…,ks为实数,且满足k1+k2+…+ks=1,证明:
k1η1+k2η2+…+ksηs也是它的解.
证 将k1η1+k2η2+…+ksηs代入方程组Ax=b的左端,得
A(k1η1+k2η2+…+ksηs)=k1Aη1+k2Aη2+…+ksAηs,由已知η1,η2,…,ηs是方程组Ax=b的解,所以Aη1=Aη2=…=Aηs=b,于是
A(k1η1+k2η2+…+ksηs)=k1b+k2b+…+ksb=(k1+k2+…+ks)b,又k1+k2+…+ks=1,得A(k1η1+k2η2+…+ksηs)=b,所以k1η1+k2η2+…+ksηs也是方程组Ax=b的解.
23.判断下列集合是否为向量空间,并说明理由:
(1)V={x=(x1,x2,…,xn)Tx1,x2,…,xn∈R满足x1+x2+…+xn=0};
(2)V={x=(x1,x2,…,xn)Tx1,x2,…,xn∈R满足x1+x2+…+xn=1}.
解 (1)因为0=(0,0,…,0)T满足x1+x2+…+xn=0,所以0∈V,即集合V非空.任取向量a=(a1,a2,…,an)T,b=(b1,b2,…,bn)T∈V,任取实数λ∈R,有
a+b=(a1+b1,a2+b2,…,an+bn)T,λa=(λa1,λa2,…,λan)T.
因为(a1+b1)+…+(an+bn)=(a1+…+an)+(b1+…+bn)=0+0=0,
λa1+λa2+…+λan=λ(a1+a2+…+an)=0,所以a+b∈V,λa∈V,即集合V对向量加法、数乘封闭,故集合V是向量空间;
(2)任取向量a=(a1,a2,…,an)T∈V,有2a=(2a1,2a2,…,2an)T.
因为2a1+2a2+…+2an=2(a1+a2+…+an)=2≠1,所以2a∉V,即集合V对向量数乘运算不封闭,故集合V不是向量空间.
24.验证:a1=(1,-1,0)T,a2=(2,1,3)T,a3=(3,1,2)T为R3的一个基,并把向量b1=(5,0,7)T,b2=(-9,-8,-13)T用这个基线性表示.
证 设A=(a1,a2,a3),B=(b1,b2).要证a1,a2,a3是R3的一个基,只需证a1,a2,
r a3线性无关,即证矩阵A可逆,利用A可逆⇔A-1A=E⇔A~E.
若求向量b1,b2用基a1,a2,a3线性表示式,就是求系数矩阵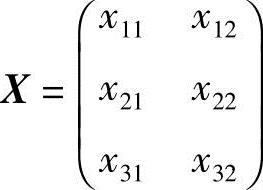 ,使得
,使得
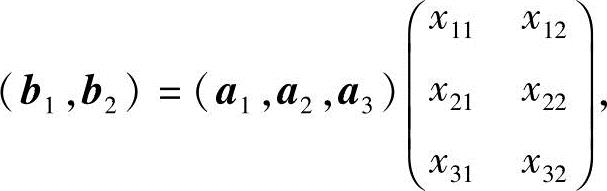
即 AX=B⇔X=A-1B⇔B~X
把以上两个问题合在一起,只需对矩阵(A,B)进行初等行变换,若子块A变成单位
阵E,则 ,即a1,a2,a3,是R3的一个基.这时,子块曰就变成系数矩阵X=A-1B.
,即a1,a2,a3,是R3的一个基.这时,子块曰就变成系数矩阵X=A-1B.

可见,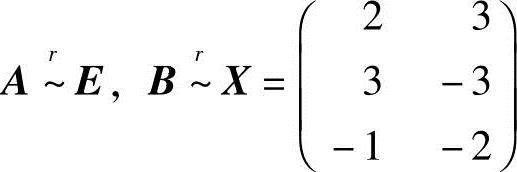 ,所以a1,a2,a3是R3的一个基,且
,所以a1,a2,a3是R3的一个基,且
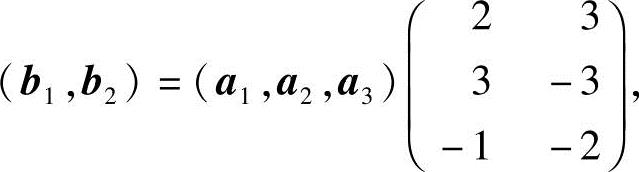
即
b1=2a1+3a2-a3,b2=3a1-3a2-2a3.
25.设向量空间R3的两个基:a1=(1,1,0)T,a2=(0,1,1)T,a3=(1,0,1)T和b1=(1,0,0)T,b2=(1,1,0)T,b3=(1,1,1)T.(1)求从基a1,a2,a3到基b1,b2,b3的过渡矩阵;(2)若向量x在基a1,a2,a3下的坐标为3,1,2,求向量x在基b1,b2,b3下的坐标.
解 (1)令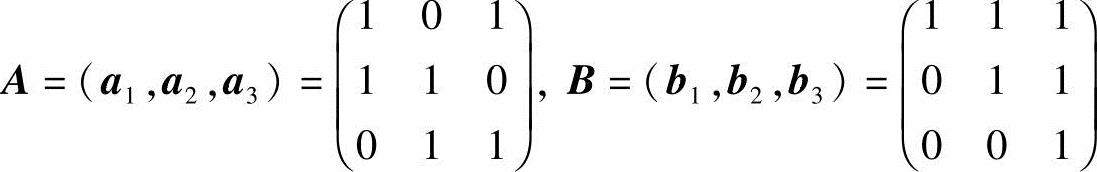 ,则从基a1,a2,
,则从基a1,a2,
rr a3到基b1,b2,b3的过渡矩阵P=A-1B,即满足A~E,B~P.
对矩阵(A,B)作初等行变换,当A变成E时,B就变成过渡矩阵P:
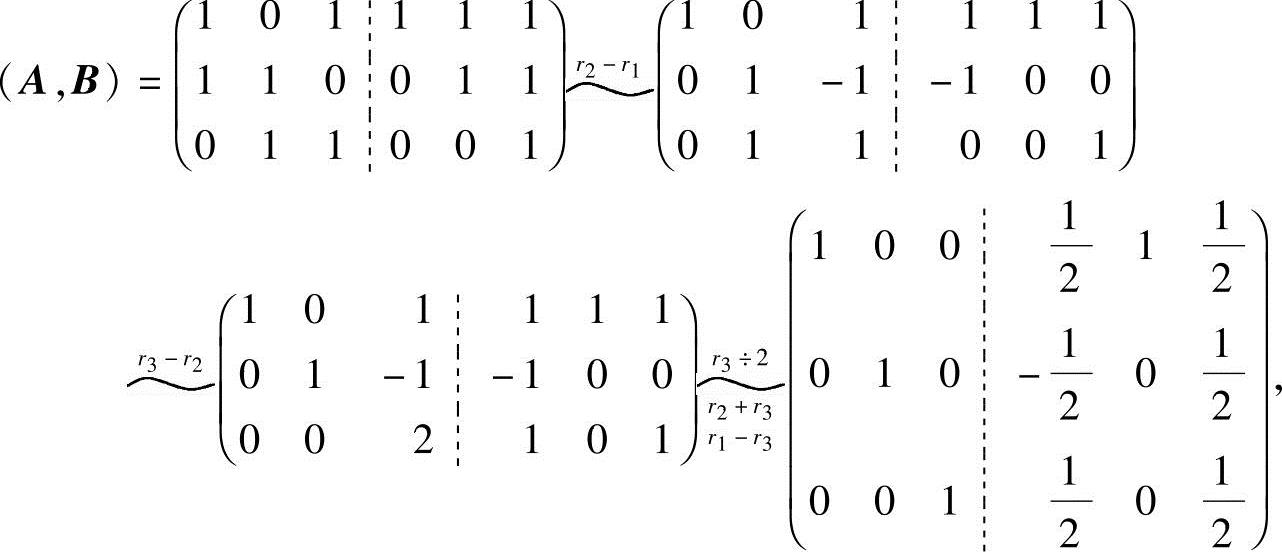
于是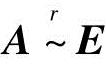 ,即A可逆,且过渡阵
,即A可逆,且过渡阵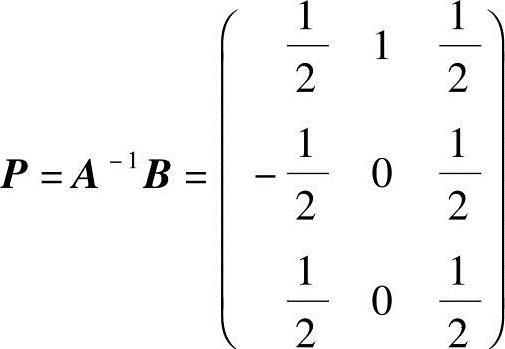 ;
;
(2)设向量x在旧基a1,a2,a3和新基b1,b2,b3下的坐标分别为y1,y2,y3和z1,z2,z3,则
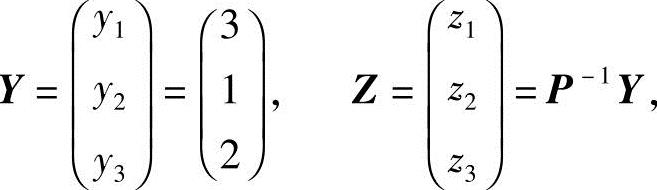
即满足 ,
,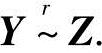
对矩阵(P,Y)作初等行变换,当P变成E时,Y就变成Z:

可见,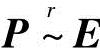 ,即P可逆,所以
,即P可逆,所以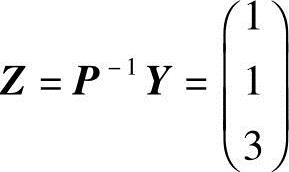 ,即向量x在基b1,b2,b3下的坐标为1,1,3.
,即向量x在基b1,b2,b3下的坐标为1,1,3.
实验4
1.设向量组A: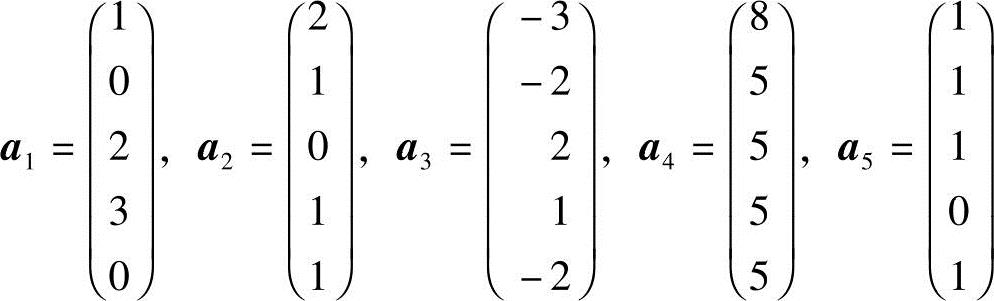 ,判断其线性相关性,给出一个最大无关组,并将其余向量用最大无关组线性表示.
,判断其线性相关性,给出一个最大无关组,并将其余向量用最大无关组线性表示.
解 在MATLAB编辑器中建立M文件如下:
a1=[1;0;2;3;0];a2=[2;1;0;1;1];a3=[-3;-2;2;1;-2];a4=[8;5;5;5;5];
a5=[1;1;1;0;1];
A=[a1,a2,a3,a4,a5];
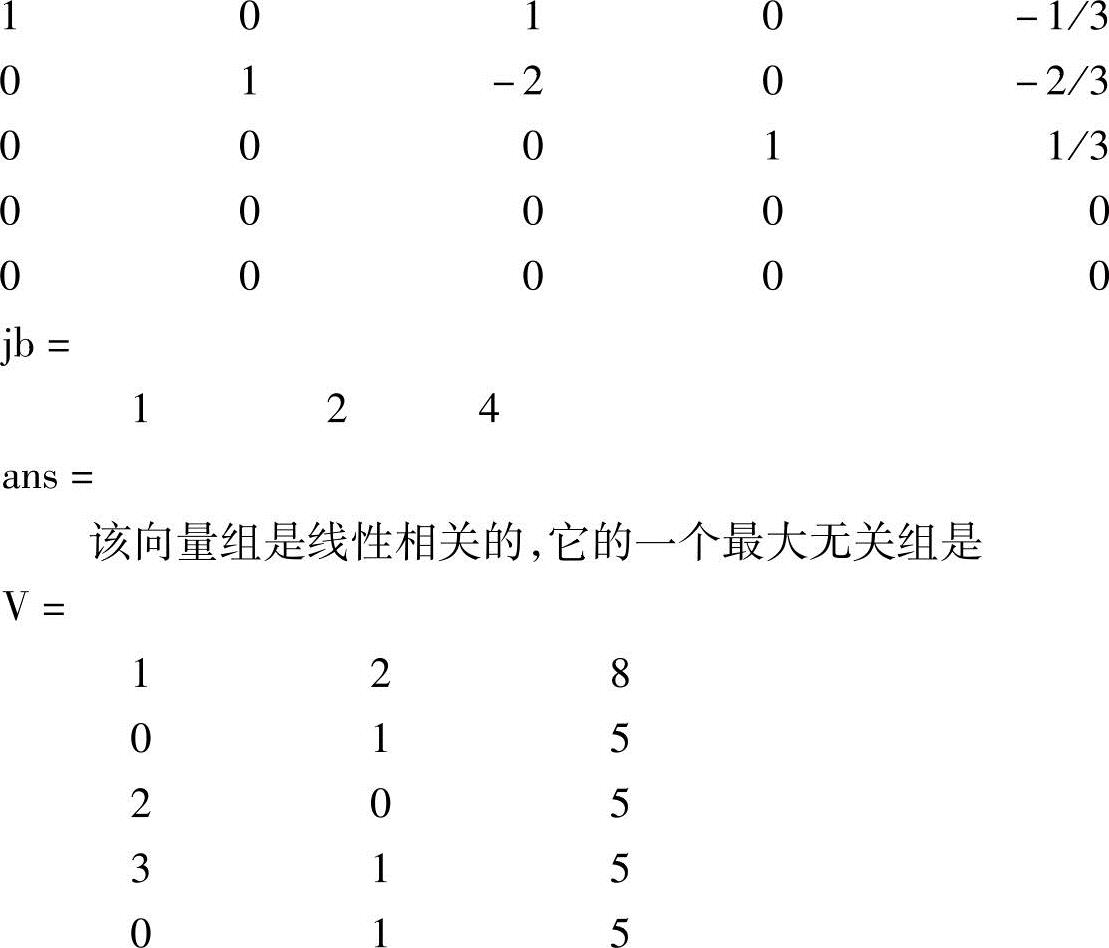
[R,jb]=rref(A) %矩阵R存放最后的行最简形,向量jb存放最大无关组中向量的
序号
len=length(jb);%输出向量jb的维数即为矩阵A的秩
iflen<5
该向量组是线性相关的,它的一个最大无关组是
V=A(:,jb)%输出向量组A的一个最大无关组
else
该向量组是线性无关的,它的唯一最大无关组就是其本身
end
运行结果为:
R=
由行最简形矩阵R知,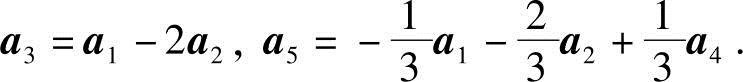
2.(教材中的例4.10)设某中药厂用9种中草药(A-I)根据不同的比例配制了7种特效药,各成分用量如表4-1(单位:g):
表 4-1
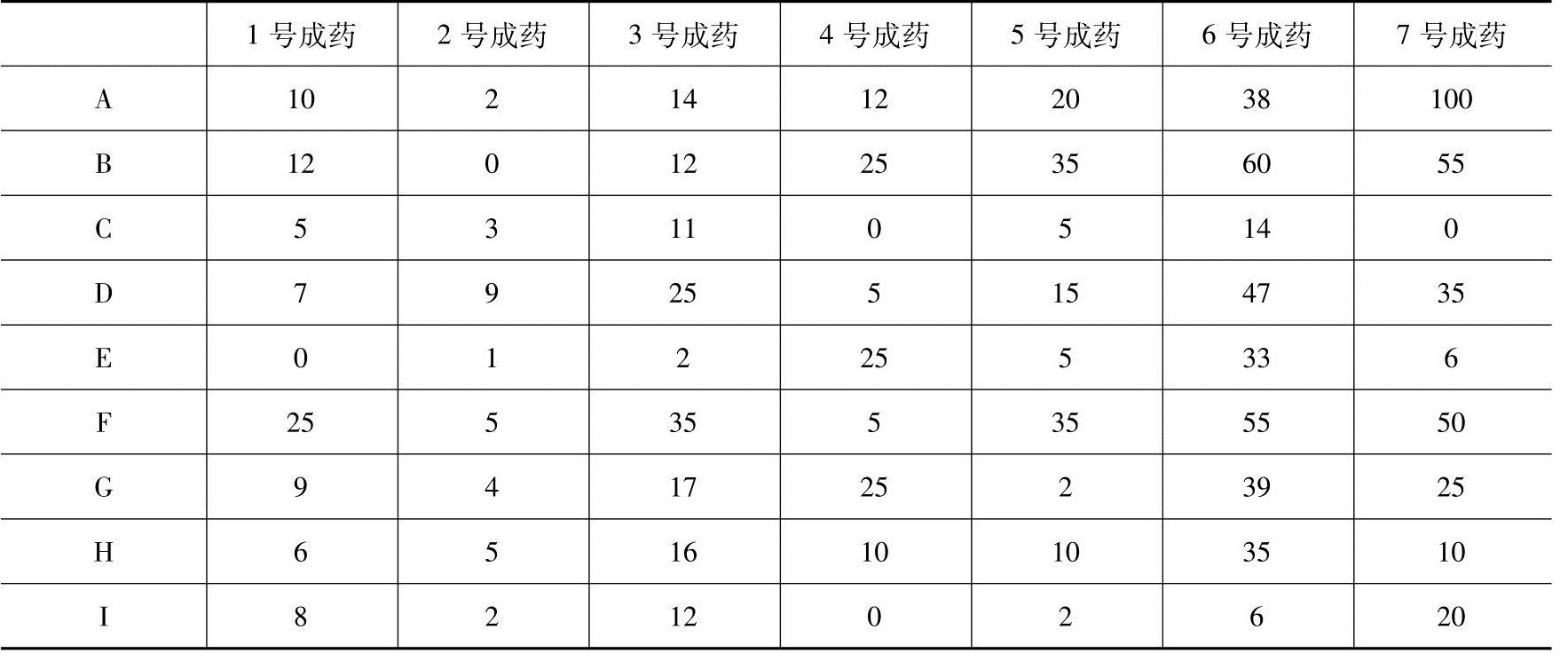
(1)某医院要购买这7种特效药,但药厂的第3号成药和第6号成药已经卖完,问能否用其他特效药配制出这两种脱销的药品?
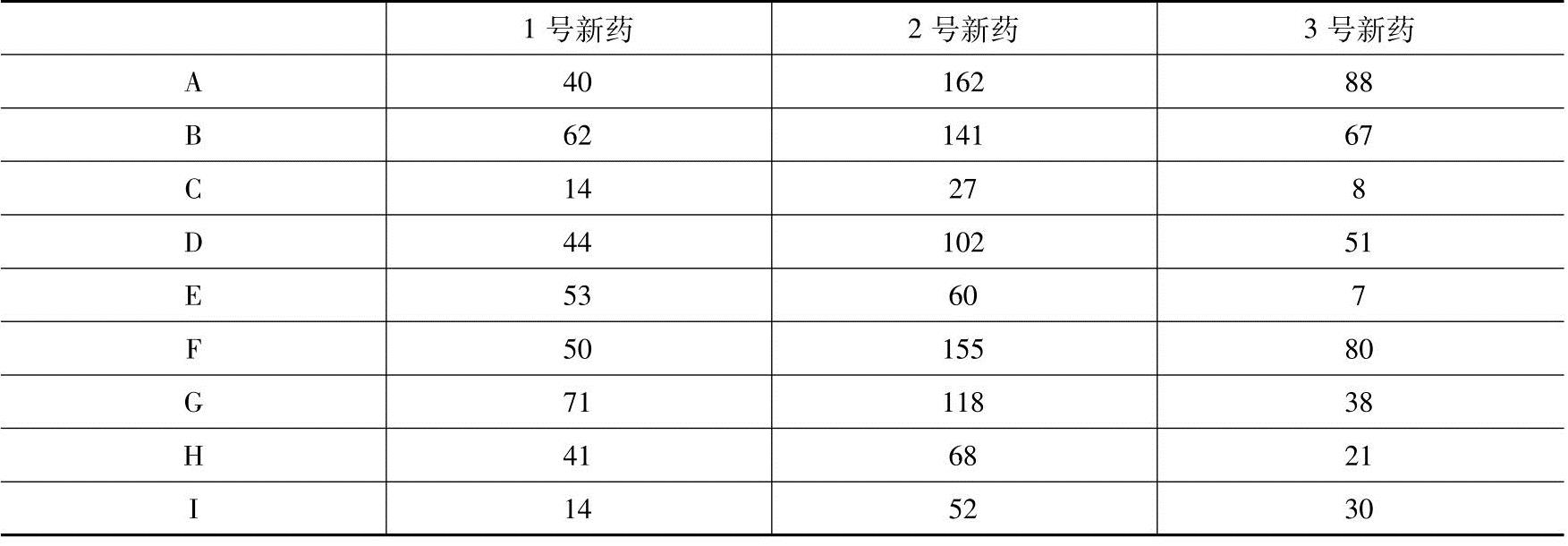
(2)现在该医院想用这7种特效药再配制3种新的特效药,表4-2是这三种新的特效药的成分,问能否配制?如何配制?
表 4-2
解 (1)方法一:

由行最简形矩阵U知,第3号成药可以用其他特效药配制,而第6号成药不可以.
方法二:
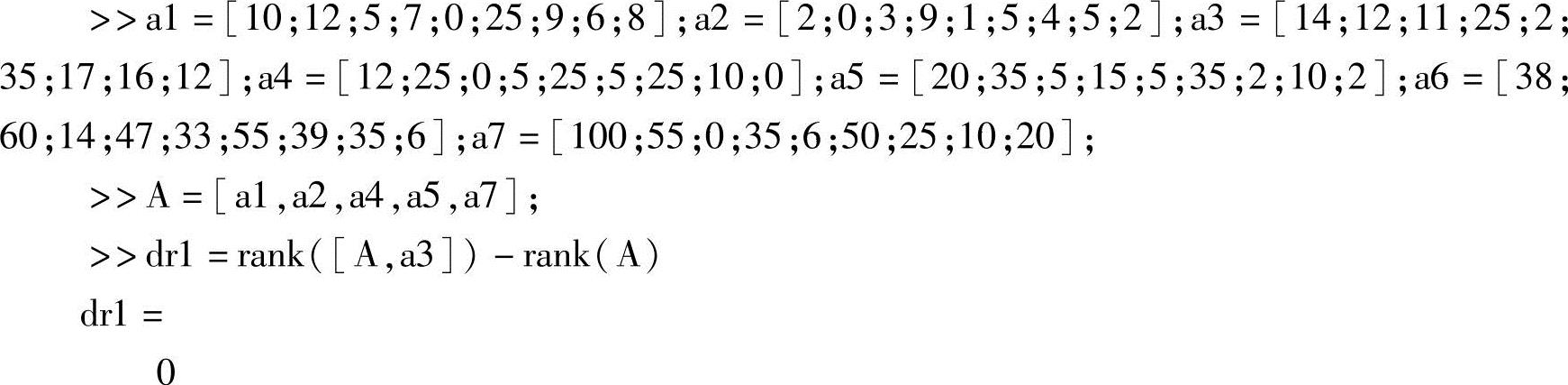
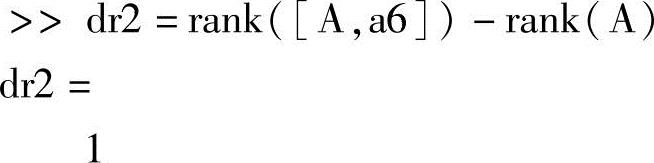
这说明,第3号成药可以用其他特效药配制,而第6号成药不可以.
(2)程序设计如下:

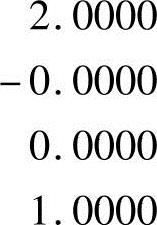
所以配制的比例可以表示为
b1=-0.5a1+1.5a3+2a4,b2=a1+2a3+2a4+a7.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




