线性代数学习辅导-问题解析

问题4.1 向量组的线性相关性和向量组线性表示问题与线性方程组有何关系？

答 （1）向量组的线性相关性体现了向量组所包含的向量之间是否存在线性关系.

向量组A：a₁，a₂，…，a_n线性相关⇔向量a₁，a₂，…，a_n之间存在某种线性关系⇔齐次线性方程组x₁a₁+x₂a₂+…+x_na_n=0有非零解；向量组A：a₁，a₂，…，a_n线性无关⇔向量a₁，a₂，…，a_n之间没有线性关系⇔齐次线性方程组x₁a₁+x₂a₂+…+x_na_n=0只有零解.

（2）向量组线性表示包括一个向量可由一个向量组线性表示；一个向量组可由另一个向量组线性表示.

1）向量b可由向量组A：a₁，a₂，…，a_n线性表示⇔非齐次线性方程组x₁a₁+x₂a₂+…+x_na_n=b有解.

2）向量组B：b₁，b₂，…，b_l可由向量组A：a₁，a₂，…，a_n线性表示⇔l个非齐次线性方程组x₁a₁+x₂a₂+…+x_na_n=b_j（j=1，2，…，l）都有解⇔矩阵方程（a₁，a₂，…，a_n）X=（b₁，b₂，…，b_l）有解.

注 当讨论向量组线性表示问题时，若向量组为无限的向量组，由于向量组与它的最大无关组（为有限的）等价，所以可用最大无关组替代无限的向量组，于是转化成情形1）或情形2）讨论.

问题4.2 两个矩阵等价与两个矩阵的行（列）向量组有何关系？

答 （1）若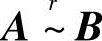，则根据矩阵的初等行变换三种类型的特点，可知矩阵A与B的行向量组等价，即两个行向量组可相互线性表示；矩阵A与B的列向量组不一定等价，但两个列向量组却有相同的线性关系.

这是因为若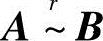，不妨设A=（a₁，a₂，…，a_n），B=（b₁，b₂，…，b_n），则在矩阵A中任取k个列向量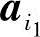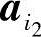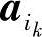，，…，所构成的矩阵与B中相对应的k个列向量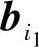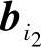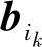，，…，所构成的矩阵也是行等价，即

所以，齐次线性方程组

与

同解，因而，向量组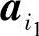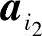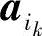，，…，与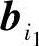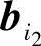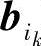，，…，有相同的线性关系.

由此可得下列结论：

1）向量组a_p1，a_p2，…，a_pr是A的列向量组的最大无关组⇔对应的向量组b_p1，b_p2，…，b_pr是B的列向量组的最大无关组.

2）A的任一列向量a_l用最大无关组a_p1，a_p2，…，a_pr线性表示的系数与B中对应的列向量b_l用最大无关组b_p1，b_p2，…，b_pr线性表示的系数相同，即

a_l=λ_1la_p1+λ_2la_p2+…+λ_rla_pr⇔bl=λ₁lb_p1+λ₂lb_p2+…+λ_rlb_pr（l=1，2，…，n）.

这也是我们在求解齐次线性方程组Ax=0、非齐次线性方程组Ax=b或求列向量组a₁，a₂，…，a_n的最大无关组，并将其余向量用这个最大无关组线性表示等问题时，要用矩阵的初等行变换将系数矩阵A、增广矩阵B=（A，b）或列向量组a₁，a₂，…，a_n所构成的矩阵（a₁，a₂，…，a_n）化成各自的行阶梯形或行最简形矩阵的原因所在.

c

（2）若A～B，则矩阵A与B的列向量组等价，即两个列向量组可相互线性表示；矩阵A与B的行向量组不一定等价，但两个行向量组却有相同的线性关系[将矩阵A与B转置，由情形（1）可推得].

（3）若A～B，即A变成B的过程中，混合使用了初等行变换和列变换，则矩阵A与B的行向量组不一定等价，列向量组也不一定等价；且它们的列向量组不一定有相同的线性关系，行向量组也不一定有相同的线性关系.因此，求矩阵的列（行）向量组的最大无关组，并用最大无关组线性表示其余向量时，不能将矩阵的初等行变换和列变换混合使用.

同理，求解齐次线性方程组Ax=0和非齐次线性方程组Ax=b时，只对系数矩阵A和增广矩阵B=（A，b）使用初等行变换，而不能使用初等列变换.(www.xing528.com)

当然，若只求矩阵的秩，则可以混合使用矩阵的初等行变换和列变换.这是因为若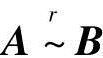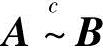，或A～B，则R（A）=R（B）.

问题4.3 判断向量组的线性相关性通常使用哪几种方法？

答 判断向量组的线性相关性是一个难点，通常使用下列四种方法.

（1）由向量组所构成的矩阵的秩判断.

1）若向量组A：a₁，a₂，…，a_n中的向量是具体的，则可用矩阵的初等行变换求秩R（a₁，a₂，…，a_n）.

特别地，若向量组所构成的矩阵（a₁，a₂，…，a_n）是方阵，则可以根据所计算的行列式a₁，a2，…，an的值是否为零，来确定秩R（a₁，a₂，…，a_n）.如，本章中的单元测试题1.（1）.

2）若向量组A：a₁，a₂，…，a_n中的向量是抽象的，则可利用矩阵秩的性质，并借助于其他矩阵的秩，求出秩R（a₁，a₂，…，a_n）.如，本章中的例4.4.

（2）利用向量组线性相关性的定义判断.

若向量组A：a₁，a₂，…，a_n中的向量是抽象的，通常根据已知条件确定齐次线性方程组x₁a₁+x₂a₂+…+x_na_n=0的解，从而确定向量组A的线性相关性.如，本章中的例4.3.

（3）利用向量组线性相关性的等价定义判断.

向量组A：a₁，a₂，…，a_n（n≥2）线性相关⇔向量组A中至少有一个向量可由其余的向量线性表示.

例如，向量b₁=a₁+a₂，b₂=a₂+a₃，b₃=a₃+a₄，b₄=a₄+a₁，则向量组b₁，b₂，b₃，b₄线性相关.这是因为向量b₄=b₁-b₂+b₃，即向量b₄可由其余向量b₁，b₂，b₃线性表示.

（4）利用与向量组线性相关性有关的结论判断.

参看知识要点中3.（1）的1）～2）和（4）的结论，利用这些结论也可以判断向量组的线性相关性.如，本章中的例4.5.

问题4.4 向量组的最大无关组有何重要作用？

答 向量组的最大无关组在不同的研究范围，扮演着不同的“角色”，具有不同的重要作用.

（1）由向量组的最大无关组等价定义可知，若A₀：a₁，a₂，…，a_r是向量组A的一个最大无关组，则向量组A与最大无关组A₀等价，且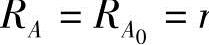r.于是，以向量组的最大无关组和秩为“桥梁”，可以将关于有限的向量组的一些重要结论（参看知识要点中2.（4））推广到无限的向量组.因此，在讨论无限的向量组的有关问题时，往往要抓住与其等价的最大无关组，因为它是有限的向量组.

（2）设n元齐次线性方程组Ax=0的解集为S（只含零解除外），则S作为含有无限多个解向量的向量组，它的最大无关组又称为齐次线性方程组的基础解系.用基础解系可以表示齐次和非齐次线性方程组的通解，从而清晰地体现了线性方程组通解的结构.

（3）设V是向量空间（零空间除外），则V作为无限的向量组，它的最大无关组又称为向量空间V的基，它的秩又称为向量空间V的维数.

设V是r维向量空间，a₁，a₂，…，a_r是向量空间V的一个基，则

V={x=λ₁a₁+λ₂a₂+…+λ_ra_rλ₁，λ₂，…，λ_r∈R}，即V可看做由它的基a₁，a₂，…，a_r所生成的向量空间，这表明了向量空间V的构造.因此，把握住基这个有限的向量组，也就把握了整个向量空间.