1.利用矩阵的初等行变换将下列矩阵化成行最简形矩阵：
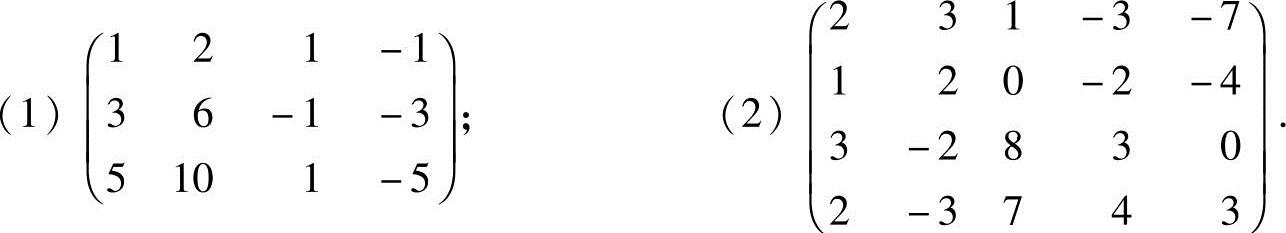
解 （1）
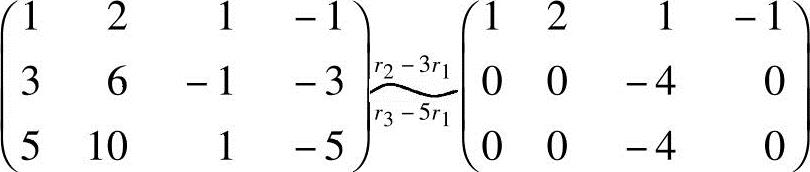
2.利用矩阵的初等变换，求下列方阵的逆阵：
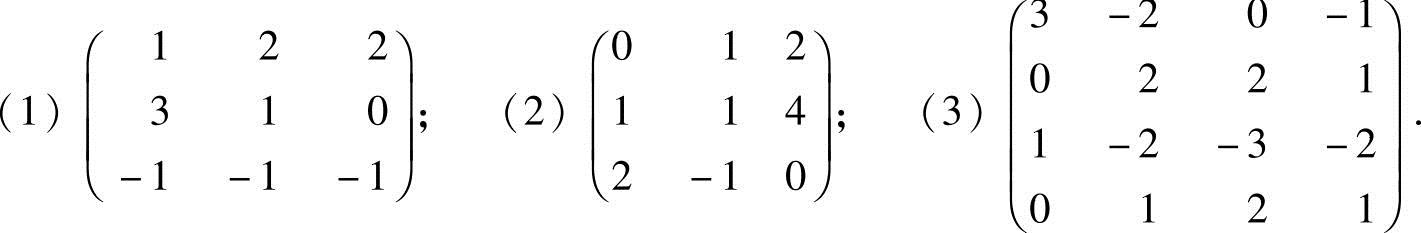
解 记所给矩阵为A，若A可逆，则A-1A=E.从而
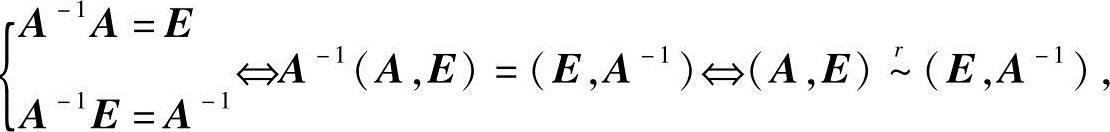
即对分块阵（A，E）作初等行变换，当A变成E时，E就变成A-1.
由于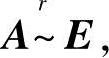
所以A可逆，且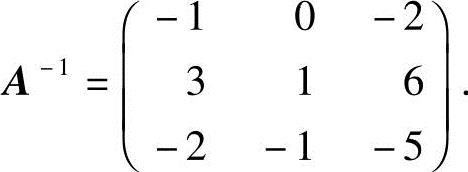
由于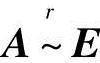
，所以A可逆，且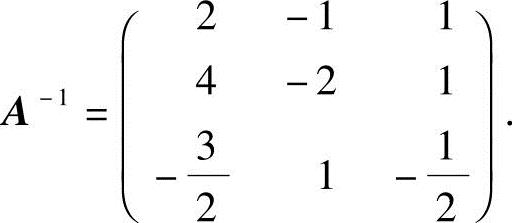
（3）
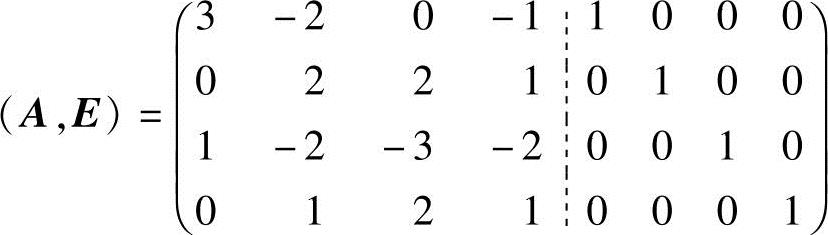
由于
，所以A可逆，且
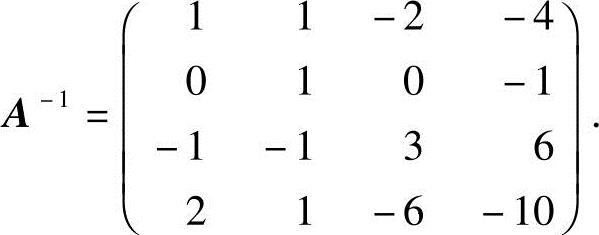
3.求解下列矩阵方程：
（1）设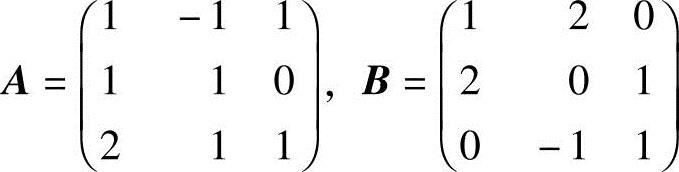
，且AX=B，求X.
（2）设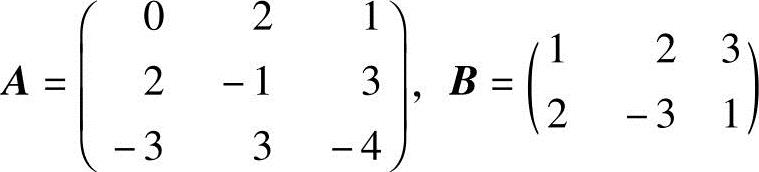
，且XA=B，求X.
解 （1）若A可逆，则X=A-1B.从而
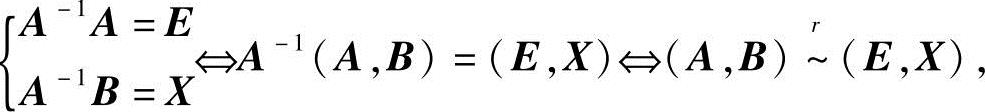
即对分块阵（A，B）作初等行变换，当A变成E时，B就变成A-1B.
由于
，所以A可逆，且
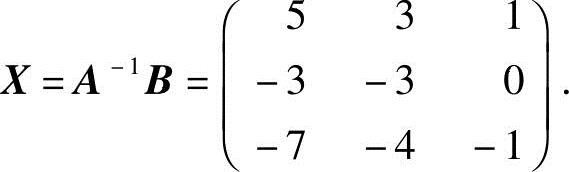
（2）因XA=B⇒ATXT=BT，若AT可逆⇒XT=（AT）-1BT，同于题（1）解法，用初等行变换先求得XT，从而求得X.
由于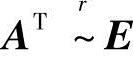
，所以AT可逆，且
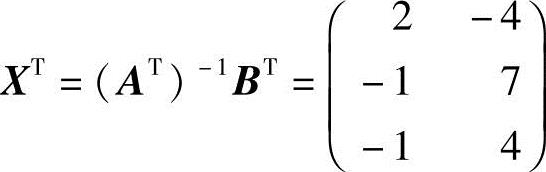，从而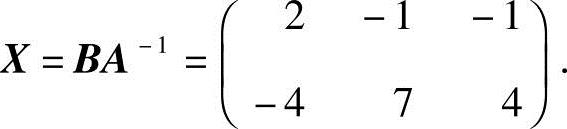
4.求下列矩阵的秩，并求它的一个最高阶非零子式：
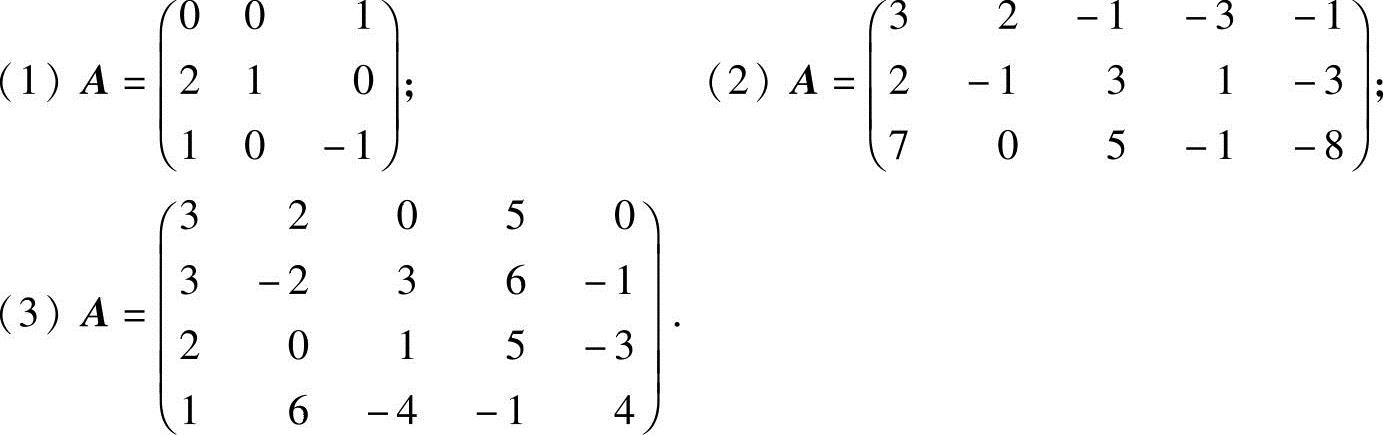
解 （1）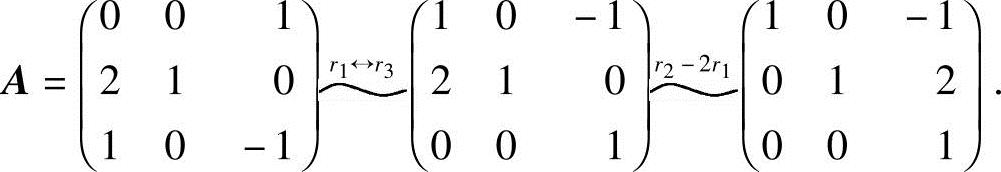
由于行阶梯形矩阵有3个非零行，所以R（A）=3.由R（A）=3，可知A的最高阶非零子式为3阶，即
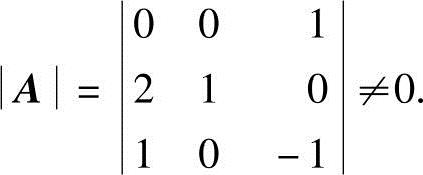
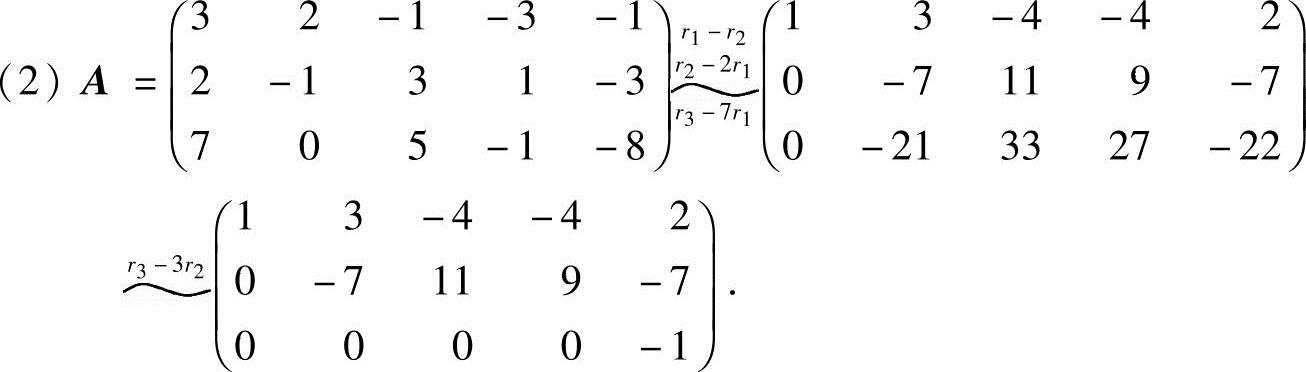
由于行阶梯形矩阵有3个非零行，所以R（A）=3.由R（A）=3，可知A的最高阶非零子式为3阶.由于3个非零行的非零首元位于第1、2、5列，故在A中的第1、2、5列可构成最高阶非零子式，即
所以R（A）=3.由于3个非零行的非零首元位于第1、2、4列，故在A中的第1、2、4列所
构成的矩阵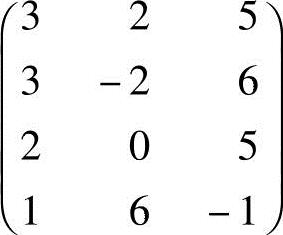
中寻找3阶非零子式，取其后三行构成的子式
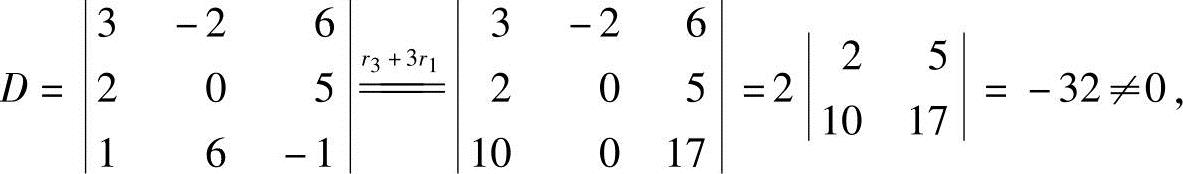
因此，这个三阶子式D就是A的一个最高阶非零子式.
5.设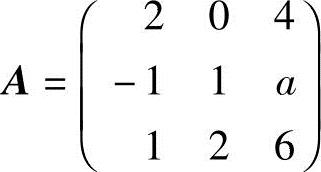
，且R（A）=2，求a.
解 对A作初等行变换.
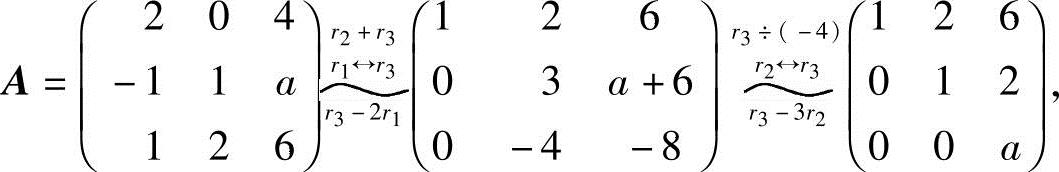
所以当a=0时，R（A）=2.
6.设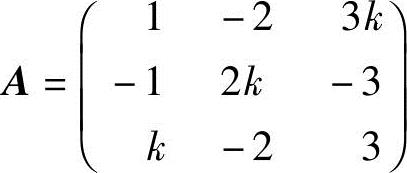
，求k，使（1）R（A）=1；（2）R（A）=2；（3）R（A）=3.
解法一 因A为三阶方阵，故R（A）=3⇔A≠0.而
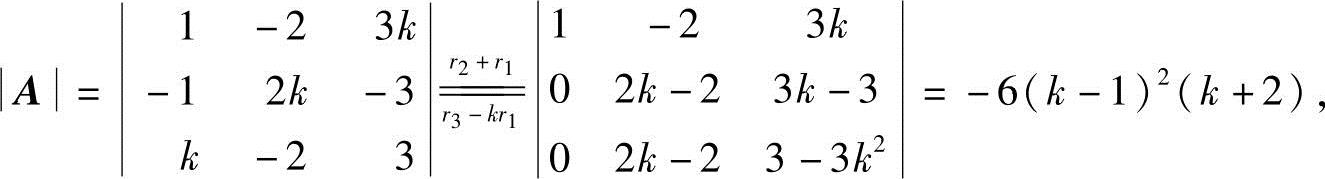
所以当k≠1且k≠-2时，R（A）=3.
当k=-2时，R（A）≤2，又A的左上角的二阶子式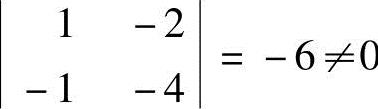
，故
R（A）≥2，所以R（A）=2.
当k=1时，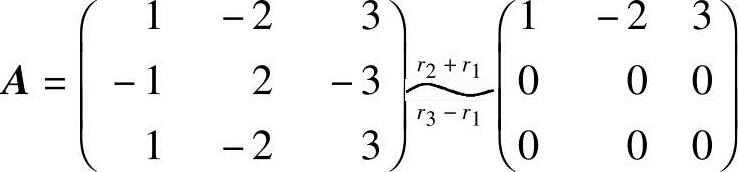
，所以R（A）=1.
解法二 对A作初等行变换.
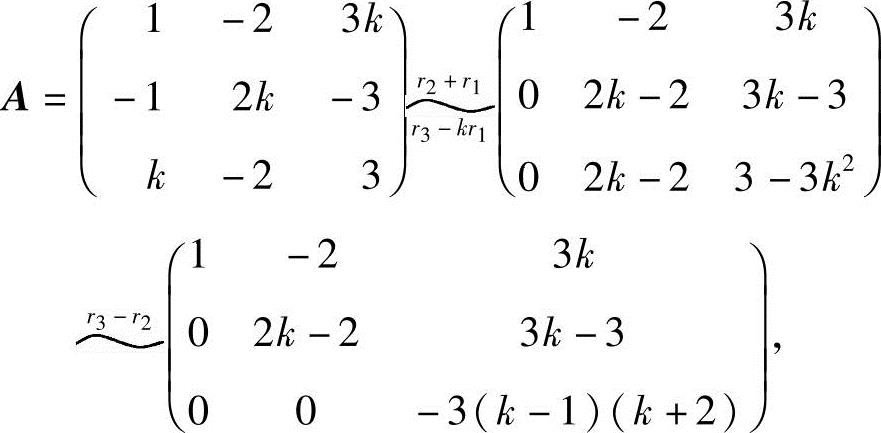
故（1）当k=1时，R（A）=1；（2）当k=-2时，R（A）=2；（3）当k≠1且k≠-2时，
R（A）=3.
7.设A，B都是m×n矩阵，证明A～B的充分必要条件是R（A）=R（B）.
证 必要性即教材中的定理3.2，所以只需证明充分性.
设R（A）=R（B）=r，则矩阵A与B有相同的标准形
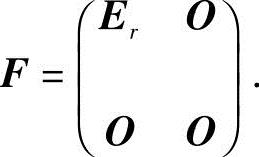
即A～F，B～F，所以由等价关系的传递性和反身性，有A～B.
8.求解下列齐次线性方程组：
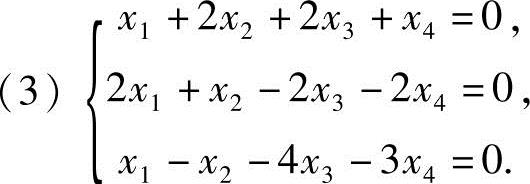
解 利用矩阵的初等行变换将系数矩阵A化成行最简形.
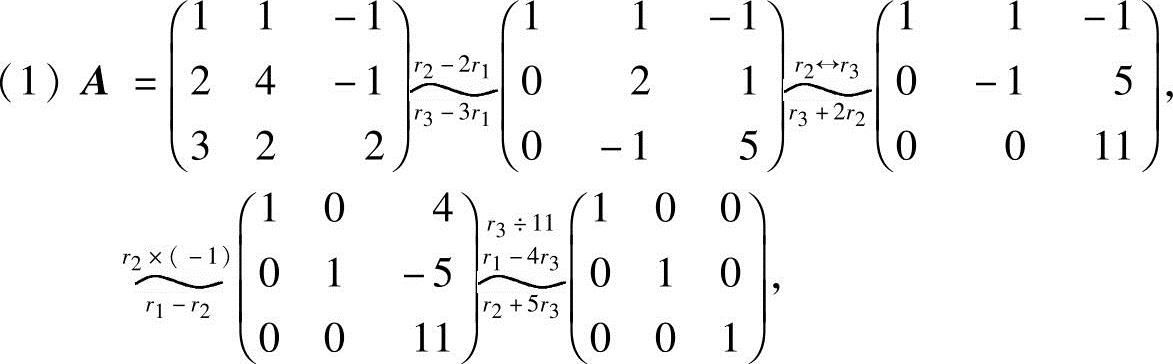
于是R（A）=3，故方程组仅有零解.
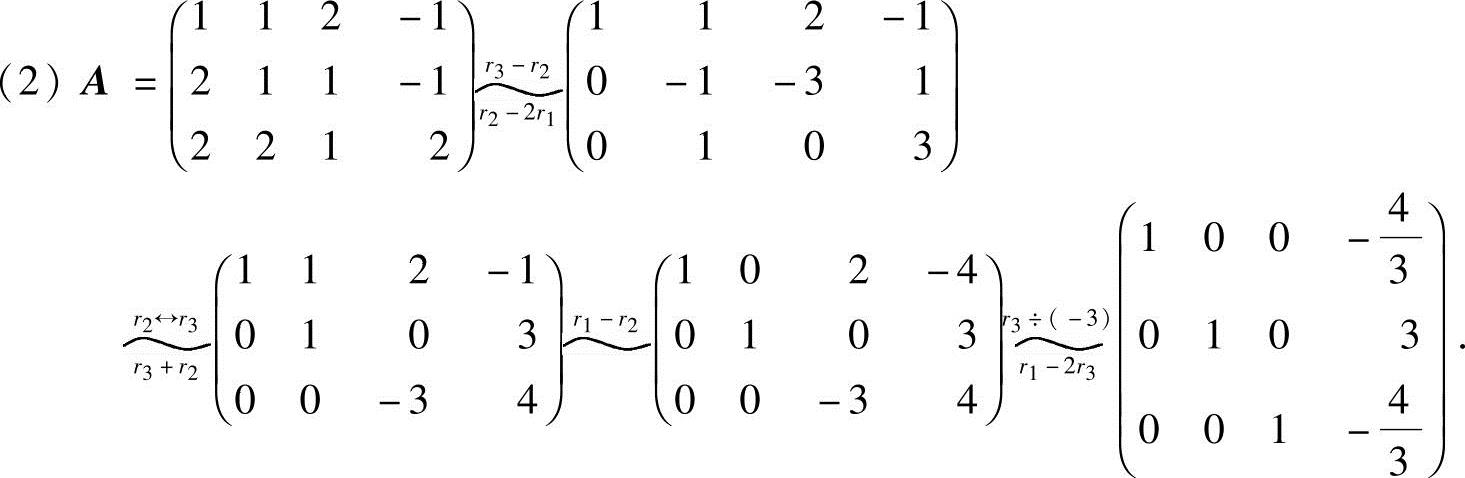
由R（A）=3<4，知方程组有非零解.取x4为自由未知数，得同解方程组
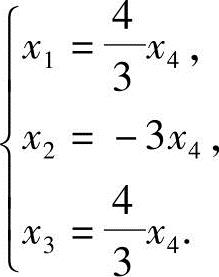
令自由未知数x4=c，得方程组的通解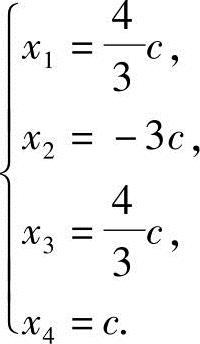
或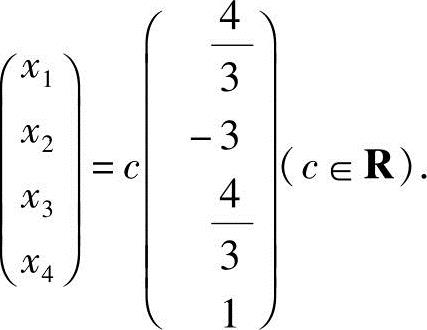
由R（A）=2<4，知方程组有非零解.取x3与x4为自由未知数，得方程组的通解
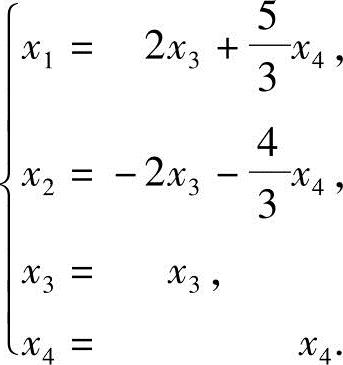
即
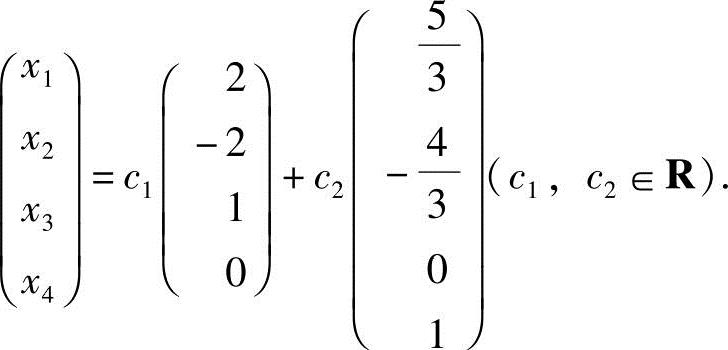
9.求解下列非齐次线性方程组：
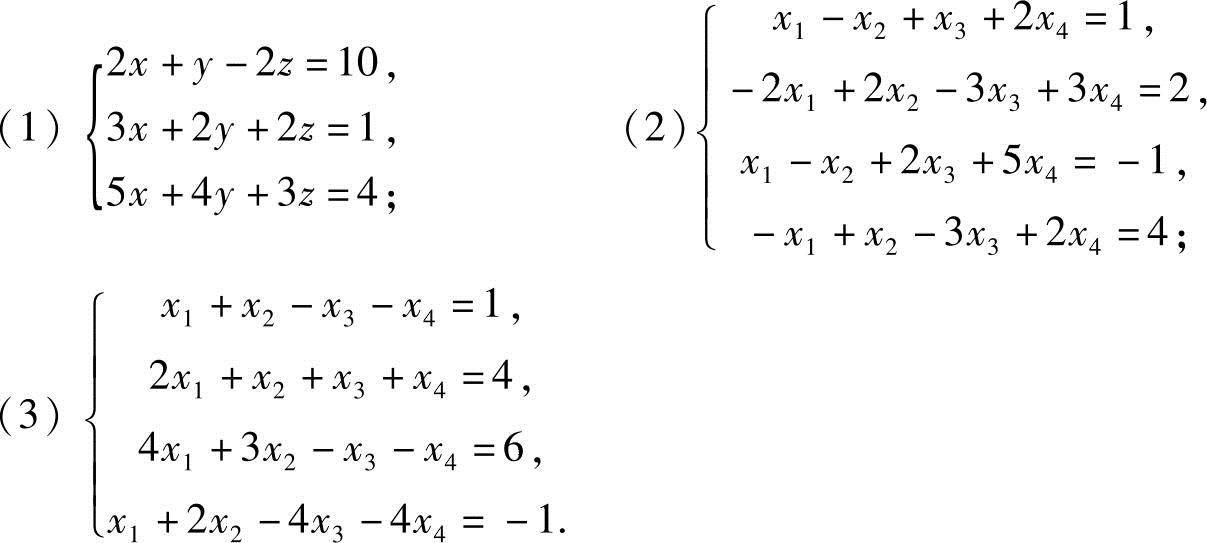
解 利用初等行变换先将增广矩阵B化成行阶梯形矩阵，有解时，再进一步化成行最简形.
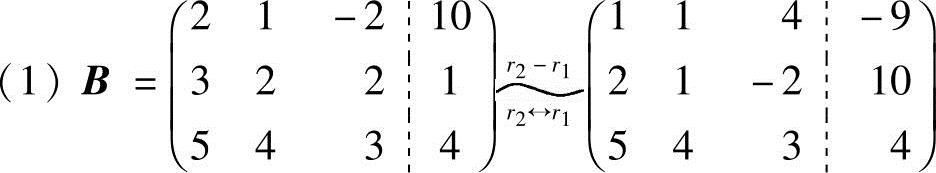
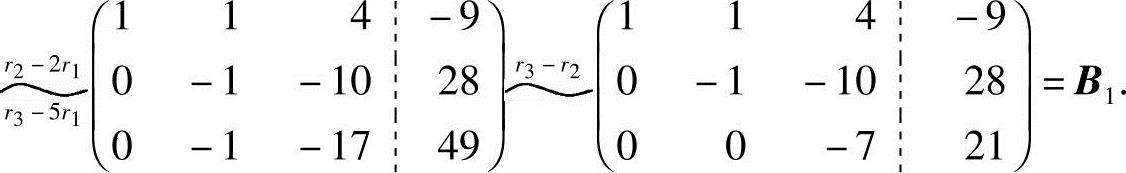
由于R（A）=R（B）=3，知方程组有唯一解，再将B的行阶梯形矩阵B1进一步化简成行最简形矩阵：
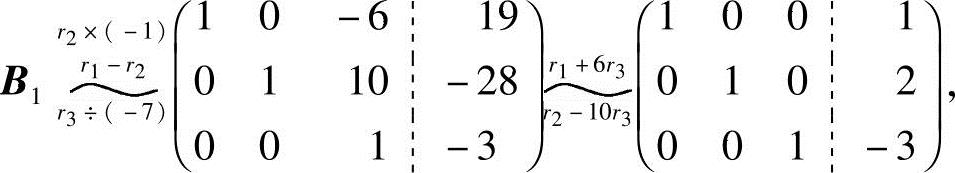
得方程组的唯一解
由于R（A）=3<R（B）=4，所以方程组无解.
由于R（A）=R（B）=2<4，所以方程组有无穷多解，得同解的方程组
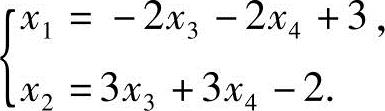
令自由未知数x3=c1，x4=c2，得方程组的通解
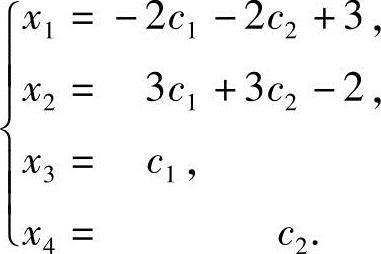
即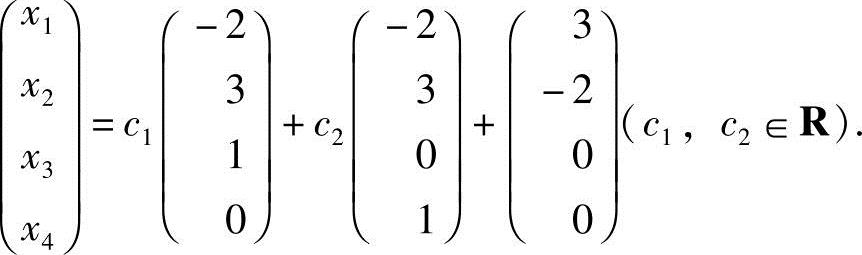
10.配平化学方程式：
Al+MnO2→Al2O3+Mn.
解 设
（x1）Al+（x2）MnO2=（x3）Al2O3+（x4）Mn.
根据配平化学方程式的原则建立数学模型，即求齐次线性方程组
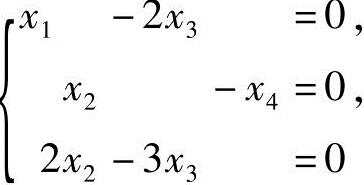
的整数解.
对系数矩阵A进行初等行变换，化为行最简形：
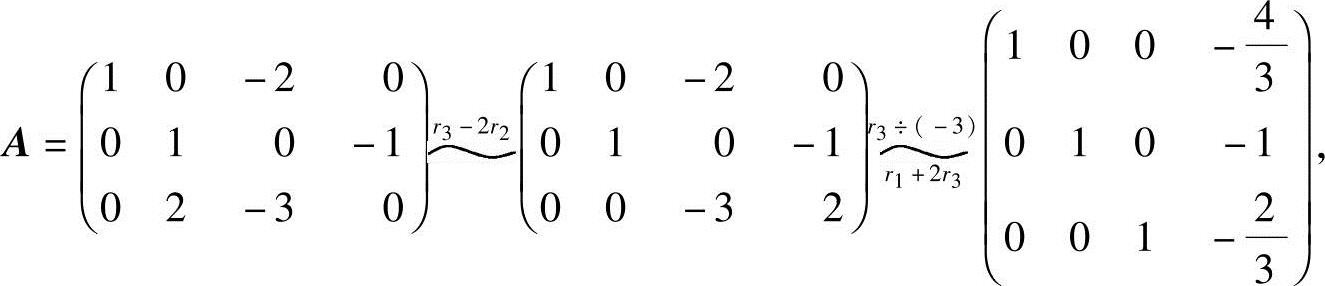
由R（A）=3<4可知方程组有非零解.取x4为自由未知数，得同解方程组
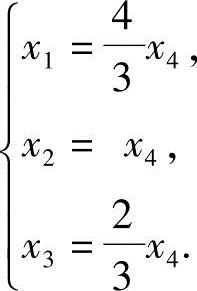
令x4=3，得x1=4，x2=3，x3=2为符合条件的解.于是化学方程式为
4Al+3MnO2=2Al2O3+3Mn.
11.设一服装厂共有三个车间，第一车间用一匹布能生产衬衣4件、长裤15条、外衣3件；第二车间用一匹布能生产衬衣4件、长裤5条、外衣9件；第三车间用一匹布能生产衬衣8件、长裤10条、外衣3件，现该厂接到一张订单，要求供应2000件衬衣、3500条长裤和2400件外衣.问如何向三个车间分配加工任务，才能完成该订单.
解 设向第一车间分配x匹布，向第二车间分配y匹布，向第三车间分配z匹布，则所求问题满足下列非齐次线性方程组：
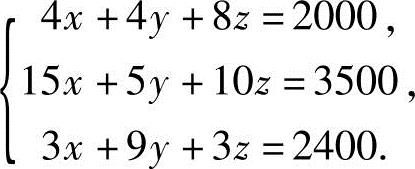
利用初等行变换将增广矩阵B化成行最简形矩阵：(www.xing528.com)
因R（A）=R（B）=3，故方程组有唯一解
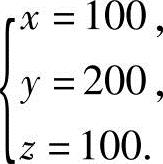
因此，向三个车间分别分配100匹布、200匹布、100匹布，才能完成该订单.
12.图3-3是某地区的灌溉渠道网，流量与流向如图所示.（1）求各段的流量；（2）若BC段渠关闭，则AD段的流量保持在什么范围内，才能使所有段的流量不超过30？
解 （1）关于灌溉渠道网的基本假设是灌溉渠道网的总流入量等于总流出量，且流入每个节点的总流量等于流出此节点的总流量.根据这一假设建立数学模型，设各路段的交通流量分别为x1，x2，x3，x4，x5，所求问题满足下列非齐次线性方程组：
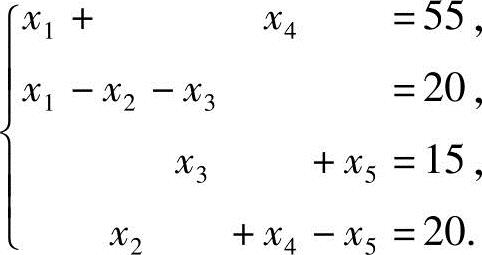
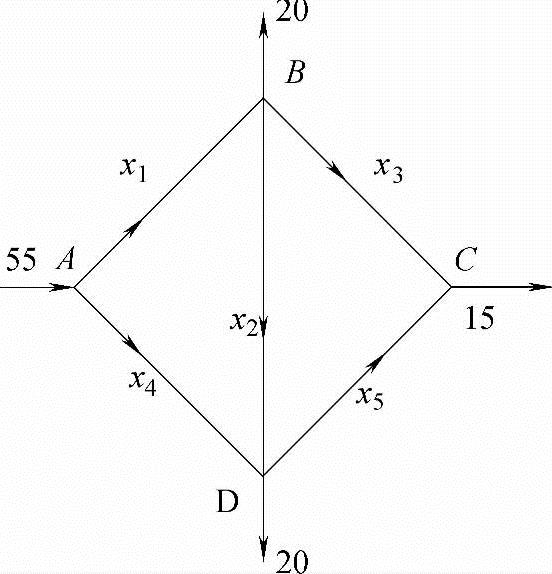
图 3-3
利用初等行变换将增广矩阵B化成行最简形矩阵：
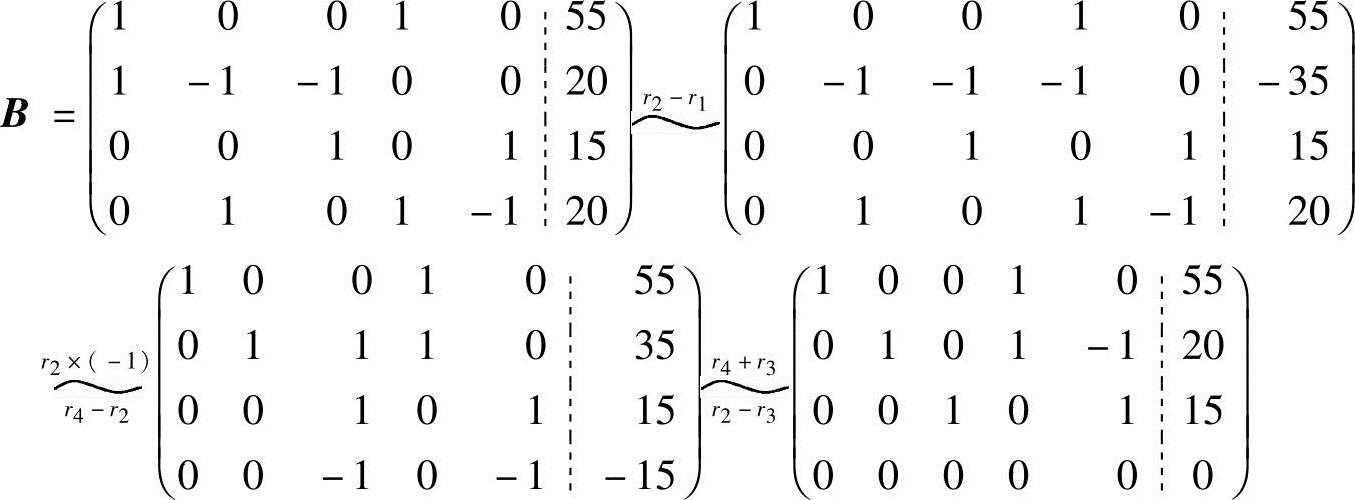
因为R（A）=R（B）=3<5，知方程组有无穷多解，得同解的方程组
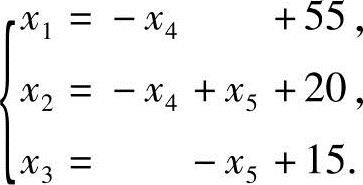
令x4=c1，x5=c2，得方程组的通解
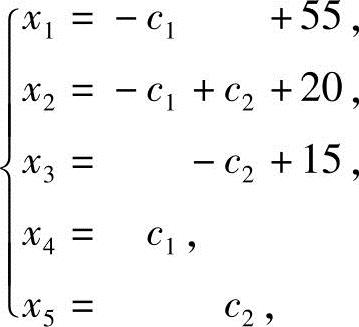
即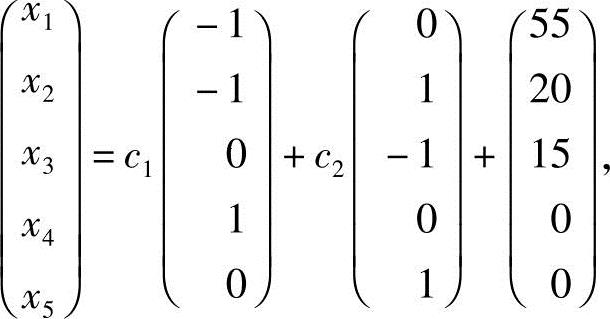
其中，c1，c2为非负整数，且满足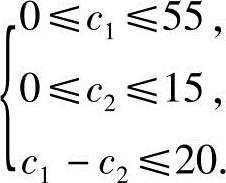
（2）若BC段渠关闭，则x3=0，x5=c2=15，得方程组的通解
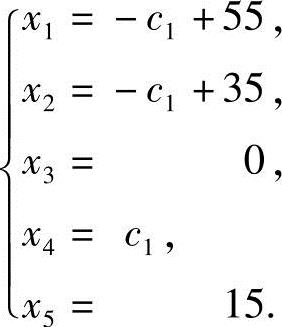
要使所有段的流量不超过30，必须满足以下不等式：
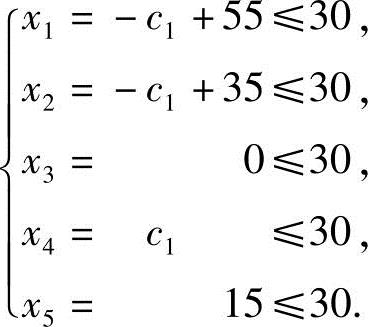
解得25≤x4=c1≤30，因此，若BC段渠关闭，则AD段的流量x4，满足25≤x4≤30，才能使所有段的流量不超过30.
13.设非齐次线性方程组
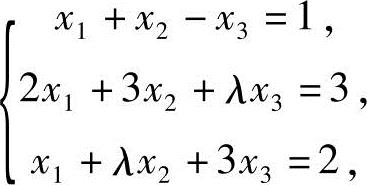
当λ为何值时，此方程组（1）有唯一解；（2）无解；（3）有无穷多解？并在有无穷多解时，求其通解.
解 利用矩阵的初等行变换，将增广矩阵B化成行阶梯形矩阵：
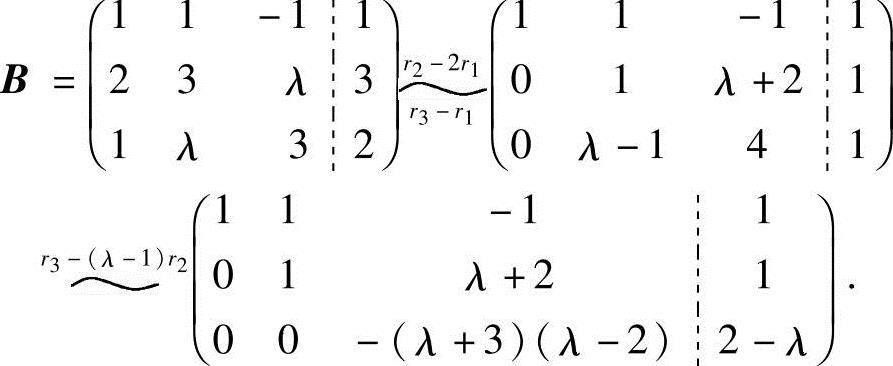
（1）当-（λ+3）（λ-2）≠0，即λ≠2且λ≠-3时，有R（A）=R（B）=3，故方程组有唯一解；
（2）当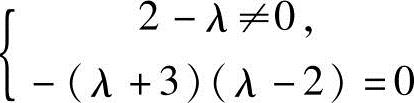
即λ=-3时，有R（A）=2<R（B）=3，故方程组无解；，
（3）当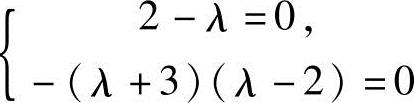
即λ=2时，有R（A）=R（B）=2<3，故方程组有无穷多，
解.此时
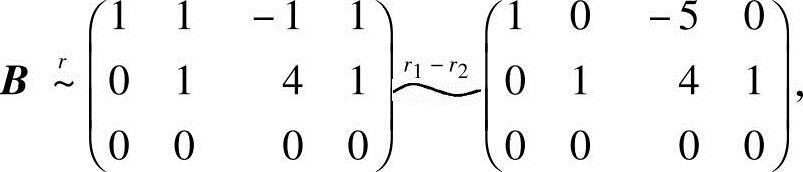
得同解的方程组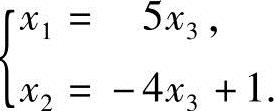
令x3=c，得方程组的通解
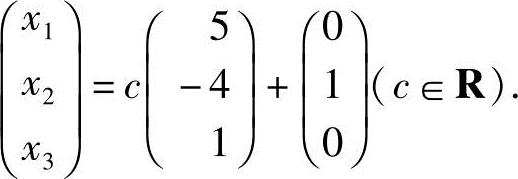
14.设非齐次线性方程组
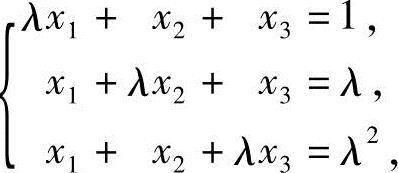
当λ为何值时，此方程组（1）有唯一解；（2）无解；（3）有无穷多解？并在有无穷多解时，求其通解.
解法一 利用矩阵的初等行变换，将增广矩阵B化成行阶梯形矩阵：
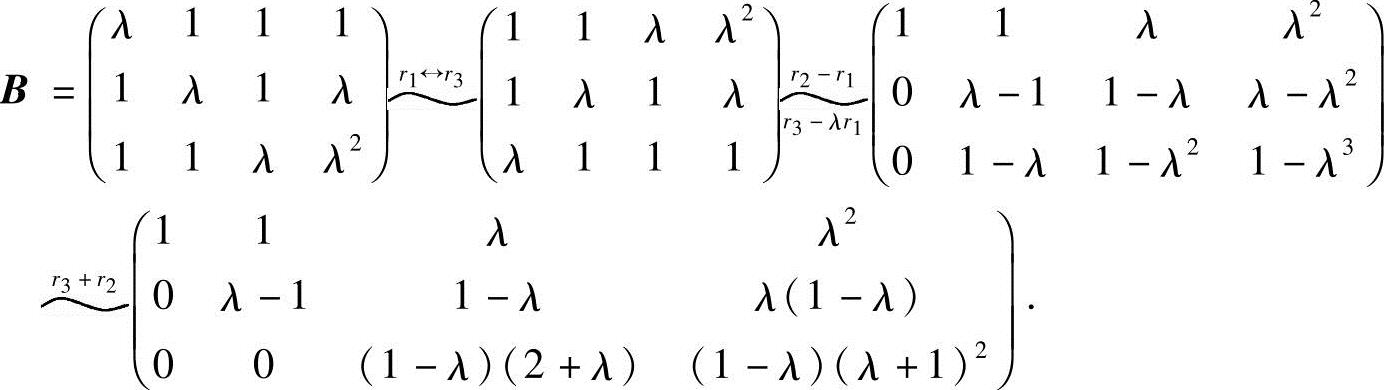
（1）当（1-λ）（2+λ）≠0，即λ≠1且λ≠-2时，有R（A）=R（B）=3，故方程组有唯一解；
（2）当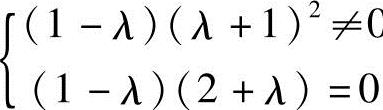
0，即λ=-2时，有R（A）=2<R（B）=3，故方程组无解；，（3）当
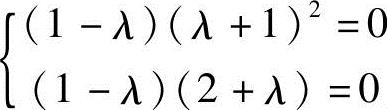，即λ=1时，有R（A）=R（B）=1<3，故方程组有无穷，多解.此时
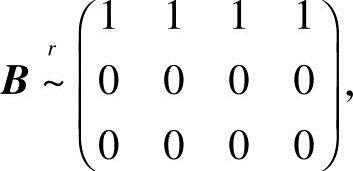
得通解
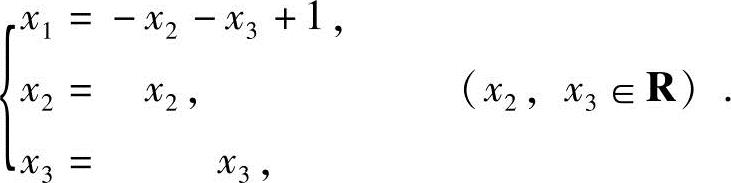
即
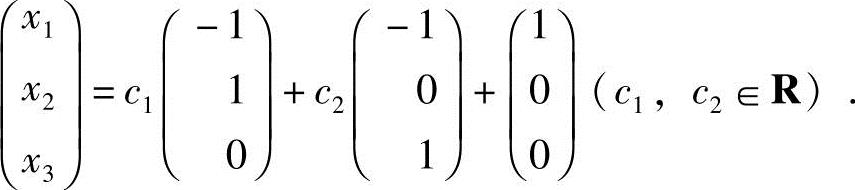
解法二 （1）因系数矩阵A为方阵，故由克拉默法则知，方程组有唯一解的充分必要条件是系数行列式A≠0.而
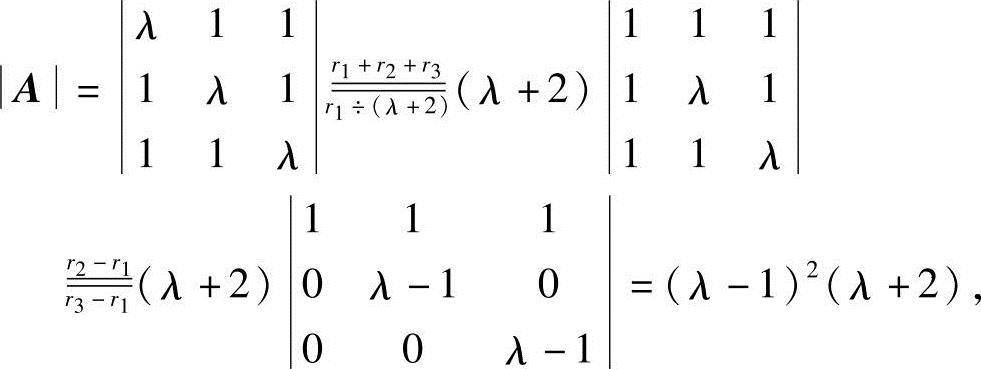
所以当λ≠1且λ≠-2时，方程组有唯一解；
（2）当λ=-2时，有
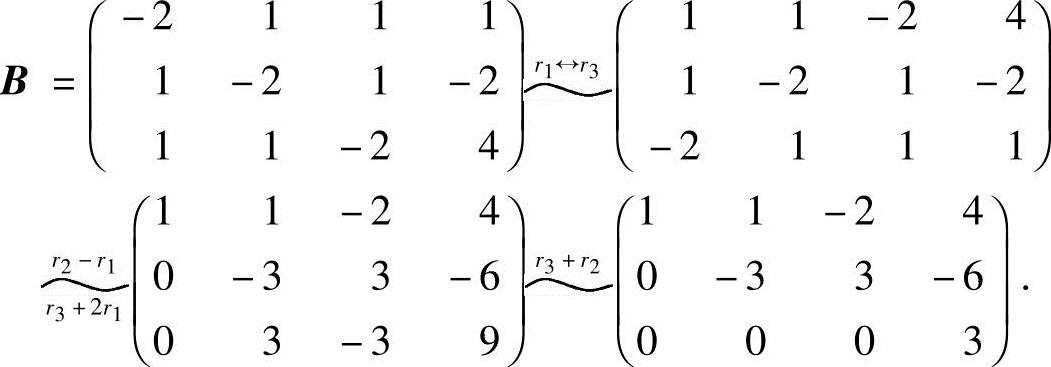
因R（A）=2<R（B）=3，故方程组无解；
（3）当λ=1时，有
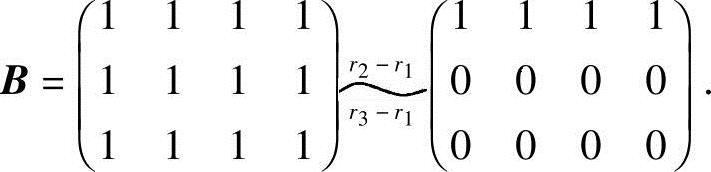
因R（A）=R（B）=1<3，故方程组有无穷多个解.得同解方程组
x1=-x2-x3+1，
令x2=c1，x3=c2，得方程组的通解
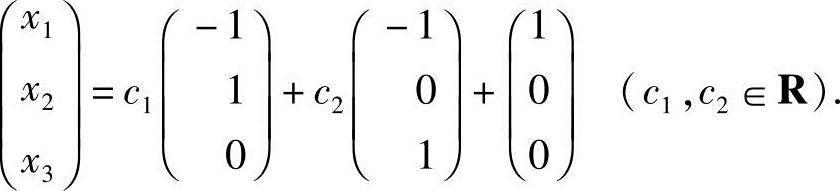
15.设非齐次线性方程组
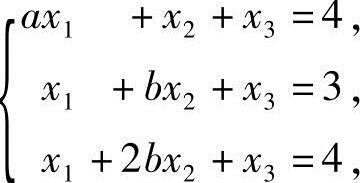
当a，b为何值时，此方程组（1）有唯一解；（2）无解；（3）有无穷多解？并在有无穷多解时，求其通解.
解 （1）因系数矩阵A为方阵，故由克拉默法则知，方程组有唯一解的充分必要条件是系数行列式A≠0.而
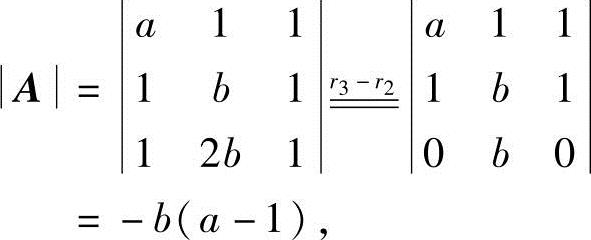
所以当b≠0且a≠1时，方程组有唯一解；
（2）当b=0时，有
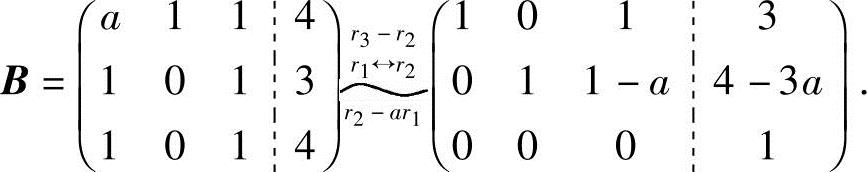
因R（A）=2<R（B）=3，故方程组无解；
（3）当a=1时，有
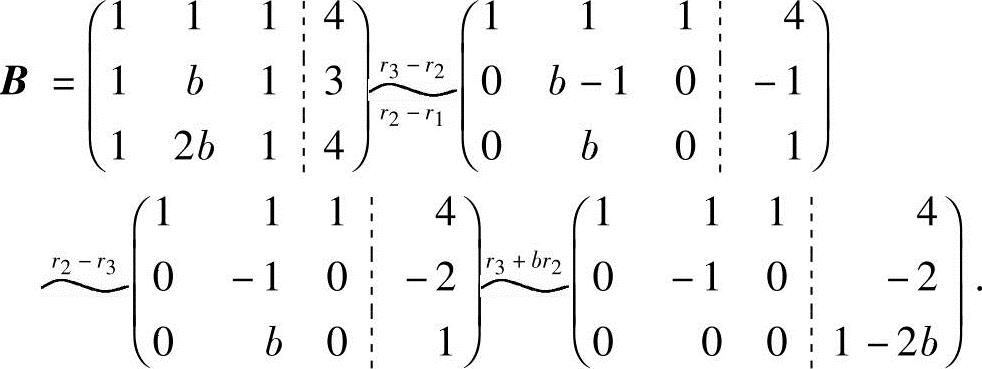
①当a=1且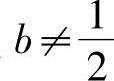
时，有R（A）=2<R（B）=3，故方程组无解；
②当a=1且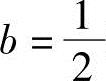
时，因R（A）=R（B）=2<3，故方程组有无穷多个解.此时
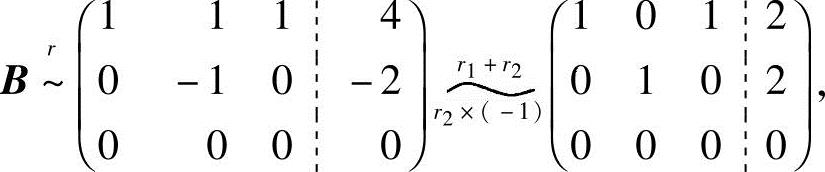
得同解的方程组
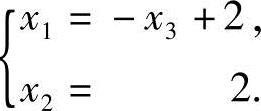
令x3=c，得方程组的通解
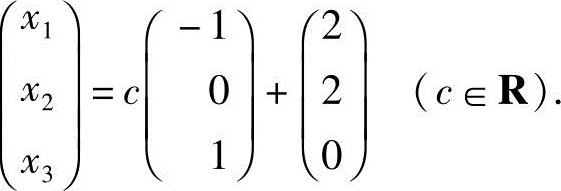
16.设A为列满秩矩阵，且AB=C，证明齐次线性方程组Bx=0与Cx=0同解.
证 若x满足Bx=0，则ABx=0，即Cx=0.
若x满足Cx=0，即ABx=0，对于齐次线性方程组Ay=0，由A为列满秩矩阵，知R（A）=未知数的个数，故由教材中的定理3.4知Ay=0只有零解，从而Bx=0.
综上即知方程Bx=0与Cx=0同解.
17.设A为m×n矩阵，证明矩阵方程AX=Em有解的充分必要条件是R（A）=m.
证 由教材中的定理3.6知，方程AX=Em有解的充分必要条件是
R（A）=R（A，Em），
而矩阵（A，Em）含m行，有R（A，Em）≤m，又R（A，Em）≥R（Em）=m，故
R（A，Em）=m，因此，方程AX=Em有解的充分必要条件是R（A）=m.
实验3
1.求齐次线性方程组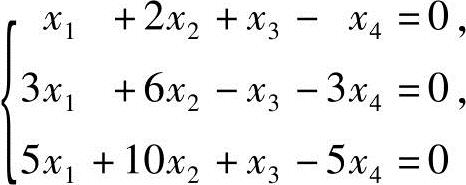
的基础解系和通解.
解 程序设计如下：
2.求线性方程组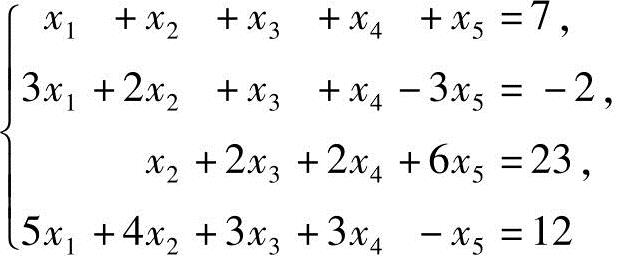
的通解.
解 在MATLAB编辑器中建立M文件如下：
所以原方程组的通解为
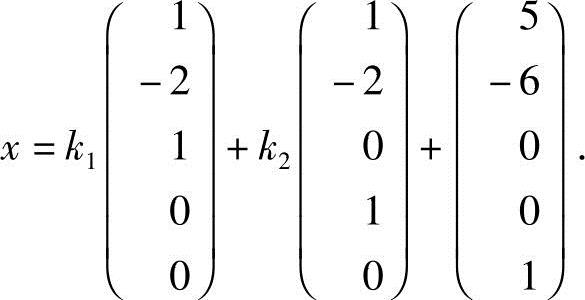
注 对于常用的或很长的程序，如果每次都从头到尾输入，则非常费时，也容易出错.将这些程序做成M文件就方便多了，只要输入自定义的命令，就可以方便的调用，编程的效率大大提高！
打开MATLAB，单击左上方File菜单项，从下拉菜单中选择New，再在弹出的菜单中选择Script，这时将生成一个未保存的M文件，当M文件写好后，依次单击File→SaveAs命令，将其存放在安装好的MATLAB的bin文件夹里面（这里注意文件名和存放目录最好都是英文的，且不要有空格）.只要在命令行窗口输入M文件名之后，敲击<Enter>键即可运行该M文件.
3.在某个城市某区域（见主教材3.4节），几条单行道彼此交叉，每个道路交叉口的交通流量（每小时过车数）简化为图3-1，其中xi（i=1，…，10）是未知流量，bi（i=1，…，13）是已观测流量，下面建立数学模型确定该交通网络未知流量.
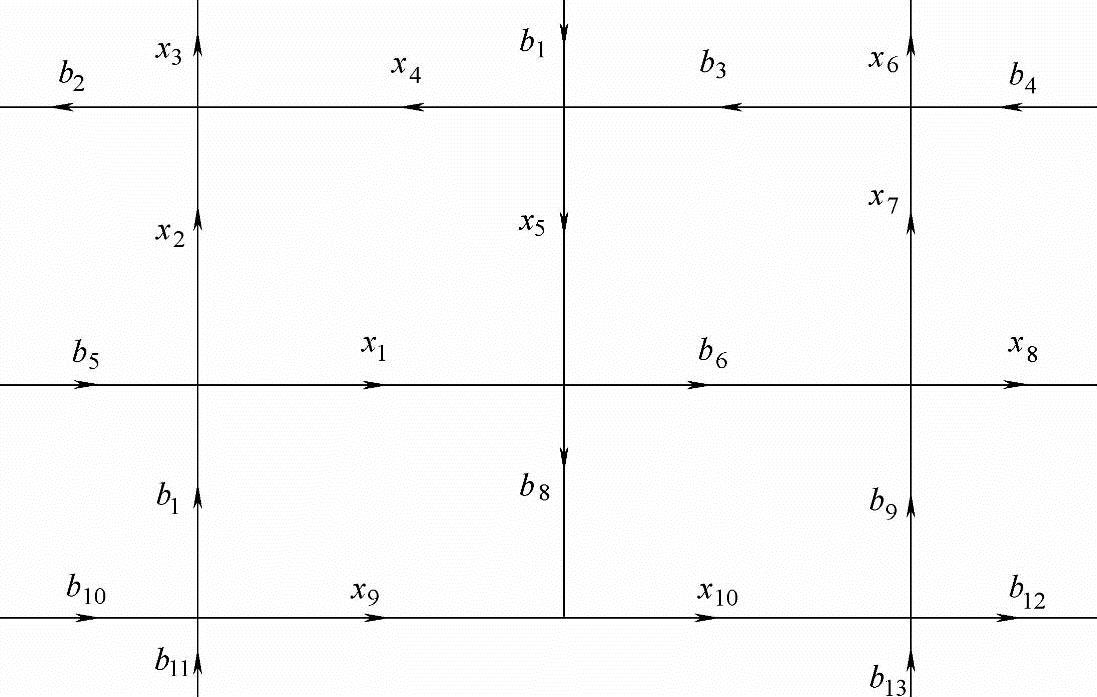
图 3-1
关于交通流量的基本假设是交通网络的总流入量等于总流出量，且流入每个节点（道路交叉口）的总流量等于流出此节点的总流量.根据这一假设建立数学模型，所求问题满足下列非齐次线性方程组：
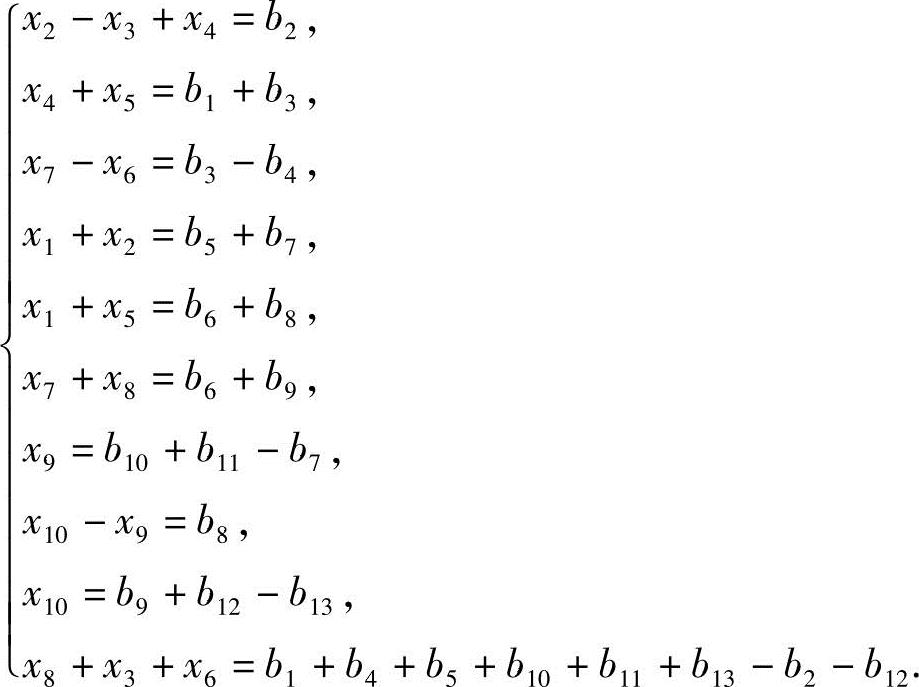
现假设已观测流量bi（i=1，…，13）分别是100，300，400，200，300，600，500，200，400，300，600，700，500.试确定该交通网络未知部分的具体流量.
解 在MATLAB编辑器中建立M文件如下：
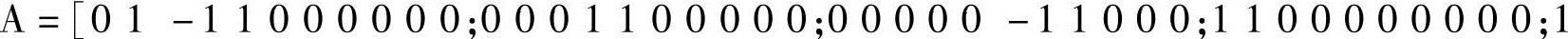
所以原方程组的通解为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
