1.填空题
(1)设 ,有初等矩阵P,Q使得PAQ=B,则P=
,有初等矩阵P,Q使得PAQ=B,则P=
,Q=.
(2)已知矩阵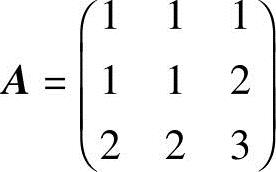 ,则R(A)=.
,则R(A)=.
(3)齐次线性方程组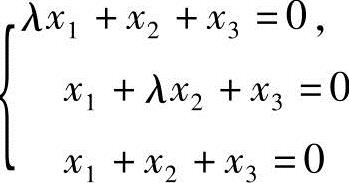 ,仅有零解,则λ应满足条件为.
,仅有零解,则λ应满足条件为.
(4)若四元线性方程组Ax=0的同解方程组是 ,则系数矩阵A的秩R(A)=
,则系数矩阵A的秩R(A)=
,自由未知量的个数有个.
(5)已知矩阵 ,B为三阶非零矩阵,且AB=O,则λ=.
,B为三阶非零矩阵,且AB=O,则λ=.
2.单项选择题
(1)设A为三阶矩阵,将A的第2行加到第1行得B,再将B的第1列的-1倍加到第2列得C,记 ,则( ).(2006年,考研,数学一)
,则( ).(2006年,考研,数学一)
(A)C=P-1AP; (B)C=PAP-1;
(C)C=PTAP; (D)C=PAPT.
(2)设A是n阶方阵,A经过若干次初等列变换变为矩阵B,则( ).
(A)A=B; (B)存在可逆矩阵P,使PA=B;
(C)存在可逆矩阵P,使PB=A; (D)存在可逆矩阵P,使BP=A.
(3)设矩阵A的秩R(A)=r,则( ).
(A)A的r-1阶子式都不为0; (B)A的r阶子式都不为0;
(C)A是一个r阶方阵; (D)A至少有一个r阶子式不为0.
(4)设A,B都是n阶非零矩阵,且AB=O,则R(A),R(B)( ).
(A)必有一个等于零; (B)都小于n;
(C)一个小于n,一个等于n; (D)都等于n.
(5)若线性方程组Ax=b中方程的个数少于未知量的个数,则有( ).
(A)Ax=b必有无穷多解; (B)Ax=0仅有零解;
(C)Ax=0必有非零解 ;(D)Ax=b一定无解.
3.设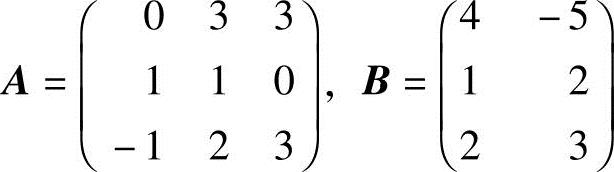 ,求满足方程AX=2X+B的矩阵X.
,求满足方程AX=2X+B的矩阵X.
4.设A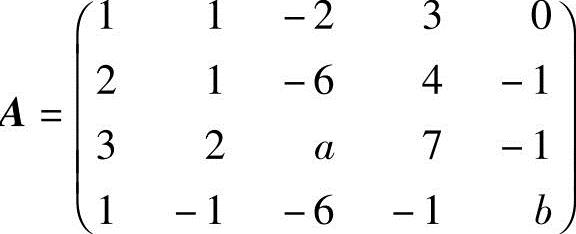 ,讨论a,b的取值,确定R(A).
,讨论a,b的取值,确定R(A).
5.解齐次线性方程组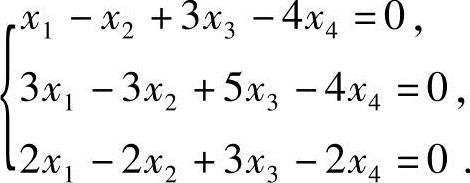
6.设线性方程组为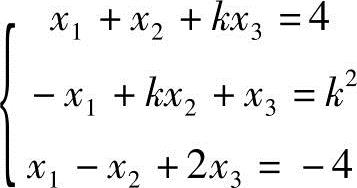 ,问:k取何值时,此方程组(1)有唯一解;(2)无解;(3)有无穷多解?在有无穷多解时求出其通解.
,问:k取何值时,此方程组(1)有唯一解;(2)无解;(3)有无穷多解?在有无穷多解时求出其通解.
7.设 ,已知线性方程组Ax=b存在两个不同的解,(1)求λ,a;(2)求方程组Ax=b的通解.(2010年,考研,数学三)
,已知线性方程组Ax=b存在两个不同的解,(1)求λ,a;(2)求方程组Ax=b的通解.(2010年,考研,数学三)
8.已知平面上三条不同直线的方程分别为(https://www.xing528.com)
l1:ax+2by+3c=0,
l2:bx+2cy+3a=0,
l3:cx+2ay+3b=0.试证这三条直线交于一点的充分必要条件为a+b+c=0.(2003年,考研,数学一)
9.设A为n阶方阵,且R(A)=1,证明: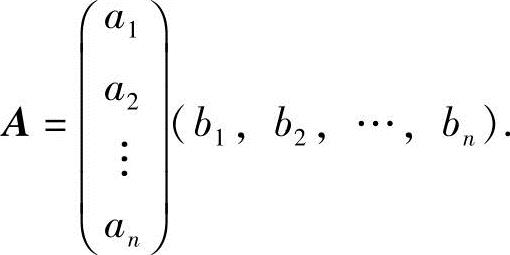
参考答案
(5)-3.提示:若R(A)=3,则A可逆,则B=O与题设矛盾,所以R(A)≤2,从而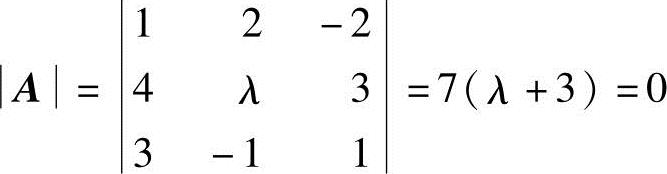 ,即λ=-3.
,即λ=-3.
2.(1)(B);提示:由题设B=PA,而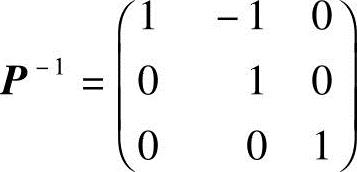 ,则有C=PAP-1.
,则有C=PAP-1.
(2)(D);(3)(D);
(4)(B);提示:A,B皆为n阶非零矩阵,即矩阵有一阶非零子式,故R(A)≥1,R(B)≥1;又由于AB=O,故R(A)+R(B)≤n(矩阵秩的性质);综上所述,有1≤R(A)≤n-1,1≤R(B)≤n-1.
(5)(C).
3.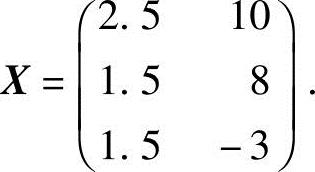
4.当a≠-8,b≠-2时,R(A)=4;当a≠-8,b=-2时,R(A)=3;
当a=-8,b≠-2时,R(A)=3;当a=-8,b=-2时,R(A)=2.
5.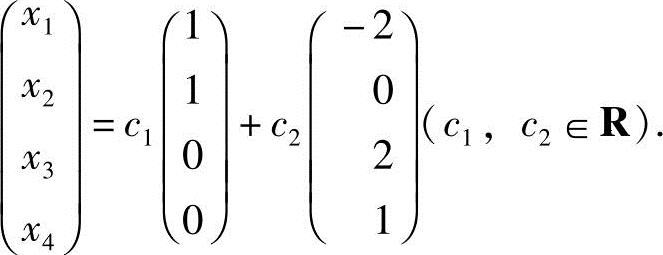
6.当k≠-1且k≠4时,方程组有唯一解;当k=-1时,方程组无解;
当k=4时,方程组有无穷多解.通解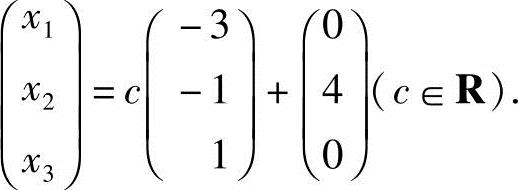
7.(1)由题意知,Ax=b的增广矩阵为
因Ax=b有两个不同的解,故R(B)=R(A)<3,即1-λ2=0,且a+1-λ=0,但λ=1时,R(A)=1<R(B)=2,方程组无解,故λ=-1,且a=-2.
(2)由(1)知
所以Ax=b的通解为k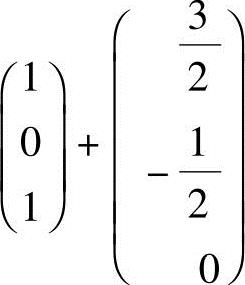 (其中k为任意常数).
(其中k为任意常数).
8.必要性:设三条直线l1,l2,l3交于一点,则线性方程组
有唯一解,故其系数矩阵A与增广矩阵B的秩均为2,于是B=0,而
=3(a+b+c)[(a-b)2+(b-c)2+(c-a)2],
根据题设(a-b)2+(b-c)2+(c-a)2≠0,故a+b+c=0.
充分性:由a+b+c=0,则从必要性的证明可知,B=0,故R(B)<3.由于
故R(A)=2.所以R(A)=R(B)=2,因此方程组(*)有唯一解,即三条直线l1,l2,l3交于一点.
9.由R(A)=1知存在n阶可逆矩阵P和Q,使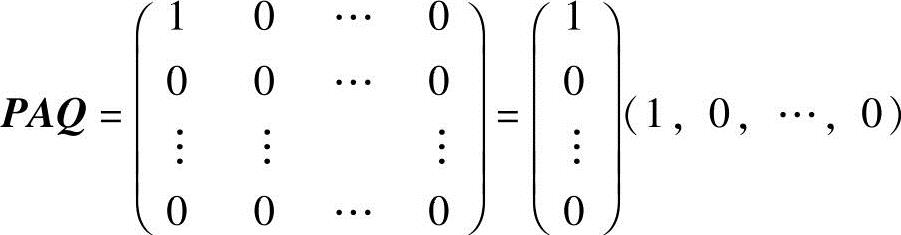 ,即
,即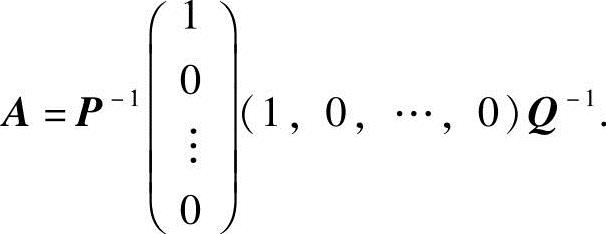
令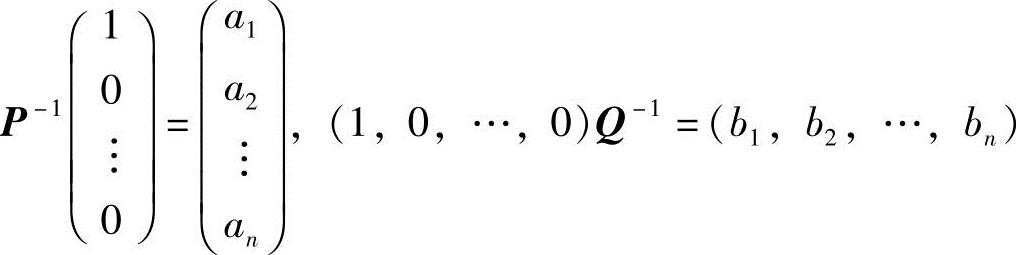 ,则
,则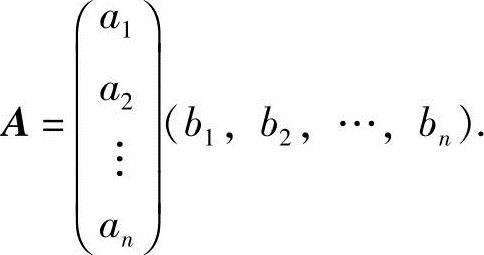
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




