线性代数学习辅导：难点解析及矩阵初等列变换问题

问题3.1 矩阵在进行初等行变换时，什么时候只需化为行阶梯形，什么时候应化为行最简形？

答 求矩阵的秩、向量组的秩与最大无关组（第4章），判断线性方程组解的情况等只需化为行梯形就可以了.

求出向量组的最大无关组，且要求将其余向量由最大无关组线性表示（第4章），则需化为行最简形，因为此时列之间的线性关系一目了然；线性方程组有解时，求出方程组的全部解，或求基础解系（第4章），最好化为行最简形以便直接写出方程组的全部解和基础解系；而当A可逆时，由（A，E）和（A，B）的行最简形就可分别求出A^-1和矩阵AX=B的解X=A^-1B.

问题3.2 引入初等矩阵的意义？

答 初等变换是对矩阵进行最基本、最重要的运算之一，而对应的初等矩阵建立了初等变换与矩阵乘法之间的联系：

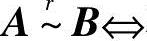存在可逆阵P，使PA=B；

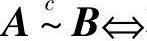存在可逆阵Q，使AQ=B；

这在理论和实用上都有着非常重要的意义.例如，用初等行变换求逆矩阵的推导和方法就是建立在这种联系基础上的.又如，利用这种关系，我们容易证明：若线性方程组Ax=b的增广矩阵B=（A，b）经有限次初等行变换化为（C，d），则线性方程组Ax=b与Cx=d是同解的.事实上，存在可逆矩阵P，使P（A，b）=（C，d），即PA=C，Pb=d，若η是Ax=b的解向量，即Aη=b，左乘P，得Cη=d，可见η也是Cx=d的解；类似可证Cx=d的解也都是Ax=b的解，所以Ax=b与Cx=d是同解的.

问题3.3 非齐次线性方程组Ax=b的系数矩阵A的秩与增广矩阵B=（A，b）的秩有什么关系？

答 令R（A）=r，R（B）=r₁，则有r≤r₁≤r+1；就是说，R（B）与R（A）要么相等（方程组有解时），要么不等（方程组无解时），最多相差1.

这是因为B是A的扩充，显然有r≤r₁，且当方程组有解时，r=r₁.下证r₁≤r+1.

设D为B=（A，b）的任意r+2阶子式（若有的话，否则显然有r₁≤r+1），若D不含B的最后一列，则D为A的r+2阶子式，由于R（A）=r，故D=0；当D含B的最后一列时，将D按这一列展开，对应的余子式都是A的r+1阶子式，也有D=0，所以R（B）=r₁≤r+1.

问题3.4 为什么不能用矩阵的初等列变换来求解线性方程组？

答 系数矩阵的列对应的是线性方程组同一未知量的系数，若交换两列，比如交换1，2列，相当于把两个未知量调换了一下位置，只要记住第几列对应的是哪个未知量，就没问题.总之，理论上是可行的，但在解具体的方程组时应避免这样做，原因是容易搞错未知量的位置.

若将某列的k（k≠0）倍加到另一列，或用数k（k≠1）乘以某一列，就行不通了，这是因为变换后的矩阵与原矩阵对应的方程组已不是同解方程组了.例如：由方程组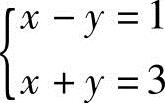，解得x=2，y=1；如果进行列变换第1列乘以1加到第2列，，则得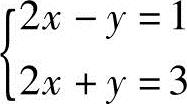，解得x=1，y=1.，(www.xing528.com)

问题3.5 在求解含有参数的线性方程组时，对增广矩阵不宜作诸如r_i×（λ+1），r_i÷（λ+1），这样的初等行变换，为什么？

答 这是因为作行变换r_i×（λ+1），当λ=-1时，相当于把矩阵第i行的元素全部变为0，这样变换后的矩阵对应的方程组与原矩阵对应的方程组不一定同解；而作行变换r_i÷（λ+1）（提取公因子λ+1），当λ=-1时，变换前第i行是零行，经变换后该行有可能变成非零行，这样变换后的矩阵的秩与原矩阵的秩未必相等，可见这两种变换可能已不再具有矩阵的初等行变换的性质了.

而不宜作行变换，原因也与上面类似.例如：

设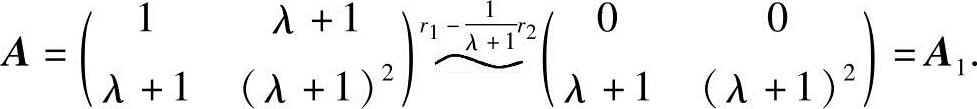

当λ=-1时，，可见R（A）≠R（A₁），A和A₁所对应的方程组也不同解.

如果作了上述三种变换，则需对λ=-1的情形另作讨论.另外，对带参数的矩阵，仍可作诸如r_i+（λ+1）r_j的初等行变换，因为当λ=-1时，相当于对第i行不作变换.

问题3.6 线性方程组的通解形式唯一吗？

答 线性方程组的通解形式并不是唯一的，这是由于自由未知数的选取不唯一.以n元齐次线性方程组Ax=0为例，设R（A）=r，只要能正确地找到n-r个自由未知数，并进一步写出含有这n-r个任意常数的通解，都是正确的.可能有人会问：究竟该把哪几个变量作为自由未知量？通常的做法是：将增广矩阵（或系数矩阵）化成行最简形，在其对应的方程组中，把每个方程中“领头”的未知量作为非自由未知量留在等号的左边，其余的未知量作为自由未知量移到等号的右边.

例如：求解齐次线性方程组

方法一（通常做法） 对系数矩阵A作初等行变换，将它变为行最简形矩阵：

取x₃，x₄为自由未知数，得通解

方法二 还可选取x₁，x₂为自由未知数，将A化为如下矩阵：

得通解