线性代数学习辅导：典型例题解析与解答

例3.1 设A是三阶方阵，将A的第1列与第2列交换得B，再把B的第2列加到第3列得到C，则满足AQ=C的可逆矩阵Q为（ ）.（2004年，考研，数学一）

分析 本题考查初等矩阵的概念与性质，对A作两次初等列变换，相当于右乘两个相应的初等矩阵，而Q即为这两个初等矩阵的乘积.

解 正确答案为（D）.由题设，有

所以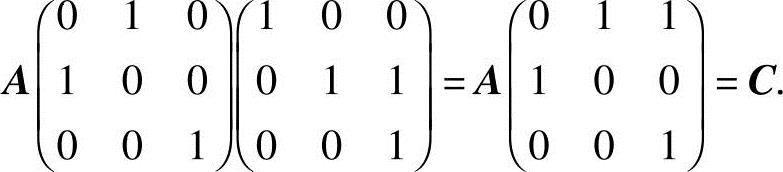可见，应选（D）.

注 涉及初等变换的问题，应掌握初等矩阵的定义、初等矩阵的性质以及其与初等变换的关系.

例3.2 设A为n（n≥2）阶可逆矩阵，交换A的第1行与第2行得矩阵B，A*，B*分别为A，B的伴随矩阵，则（ ）.（2005年，考研，数学一）

（A）交换A*的第1列与第2列得B*； （B）交换A*的第1行与第2行得B*；

（C）交换A*的第1列与第2列得-B*；（D）交换A*的第1行与第2行得-B*.

解 正确答案为（C）.由题设，存在初等矩阵E（1，2）（交换n阶单位矩阵的第1行与第2行所得），使得E（1，2）A=B，于是

B^-1=A^-1E（1，2）-1=A^-1E（1，2），因此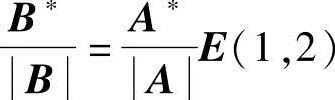，，又因为A=-B，所以A*E（1，2）=-B*.可见，应选（C）.

例3.3 设A为m×n矩阵，Ax=0是非齐次线性方程组Ax=b所对应的齐次线性方程组，则下列结论中正确的是（ ）.

（A）若Ax=0仅有零解，则Ax=b有唯一解；

（B）若Ax=0有非零解，则Ax=b有无穷多解；

（C）若Ax=b有无穷多解，则Ax=0仅有零解；

（D）若Ax=b有无穷多解，则Ax=0有非零解.

解 正确答案为（D）.首先看（A）.若Ax=0仅有零解，则R（A）=n.但不能保证R（A，b）=R（A）=n，所以排除（A）.同理（B）也不对.再看（C）.若Ax=b有无穷多解，则R（A，b）=R（A）<n，由于R（A）<n，所以Ax=0有非零解.可见，也应排除（C），故选（D）.

注 本题考察的是Ax=0与Ax=b的解之间的关系，应掌握齐次和非齐次线性方程组解的判定定理.

例3.4 非齐次线性方程组Ax=b中未知量个数为n，方程个数为m，R（A）=r，则（ ）.（1997年，考研，数学四）

（A）r=m时，方程组Ax=b有解；

（B）r=n时，方程组Ax=b有唯一解；

（C）m=n时，方程组Ax=b有唯一解；

（D）r<n时，方程组Ax=b有无穷多解.

解 正确答案为（A）.由题设知A为m×n矩阵，首先看（A）.当r=m，即R（A）=m时，由秩的性质知，R（A）≤R（A，b）≤m，故R（A）=R（A，b）=m，所以（A）正确.当r=n时，A列满秩；m=n时，表示A为方阵；r<n时，这些都不能保证R（A）=R（A，b），所以（B）、（C）、（D）都可排除.

例3.5 设齐次线性方程组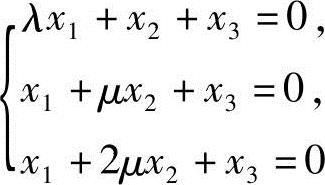有非零解，则λ=，或μ=.

解n元齐次线性方程组Ax=0有非零解⇔R（A）<n，而当A是方阵时，R（A）<n⇔|A|=0.因

所以当λ=1或μ=0时，A=0，即Ax=0有非零解.

例3.6 设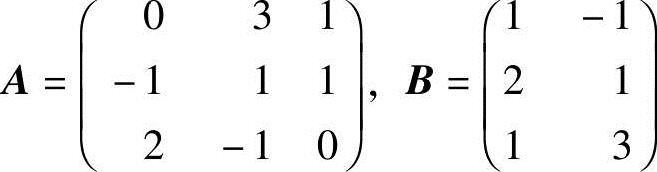，且X=AX+B，求矩阵X.

解 由X=AX+B，得（E-A）X=B.

若E-A可逆，则X=（E-A）-1B.从而

即对分块阵（E-A，B）作初等行变换，当E-A变成E时，B就变成（E-A）-1B.

可见E-A～E，所以E-A可逆，且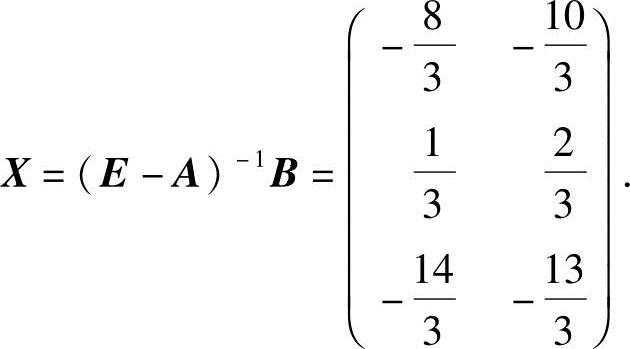

例3.7 求矩阵的秩.

解 将矩阵A进行初等行变换有

由于初等变换不改变矩阵的秩，所以R（A）=R（B），显然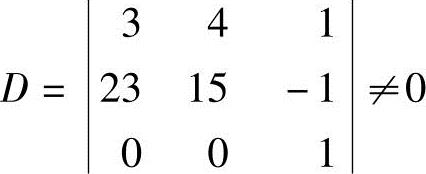是B中一个最高阶非零子式，因此R（A）=R（B）=3.

注 求矩阵的秩的方法有定义法和初等行变换法.一般来说，用定义法，需要找出不为零的最高阶子式，而这么做计算量是较大的，本题将两种方法进行了综合使用，先作初等变换，等运算到某一步再找最高阶非零子式，这种做法往往会简便些.

例3.8 设A为n阶矩阵，且A²=E，证明R（A-E）+R（A+E）=n.

证 因（E-A）+（A+E）=2E，故R（E-A）+R（A+E）≥R（2E）=n[利用了矩阵秩的

性质：R（A+B）≤R（A）+R（B）]；(www.xing528.com)

由于R（E-A）=R（A-E），因此R（A-E）+R（A+E）≥n；

又A²=E，即（A-E）（A+E）=O，所以R（A-E）+R（A+E）≤n[利用了矩阵秩的性

质：A_m×n^Bn×l=O⇒R（A）+R（B）≤n].

综合上述，n≤R（A-E）+R（A+E）≤n，得R（A-E）+R（A+E）=n.

例3.9 设有齐次线性方程组

试问a取何值时，该方程组有非零解，并求出其通解.（2004年，考研，数学一）

分析 本题中的齐次线性方程组，其方程的个数与未知量的个数相同，因此可考虑对系数矩阵直接用初等行变换化为阶梯形，再讨论其秩是否小于n，进而判断是否有非零解；或直接计算系数矩阵的行列式，再根据题设行列式的值必为零，由此对参数a的可能取值进行讨论.

解 对方程组的系数矩阵A作初等行变换，有

当a=0时，R（A）=1<n，故方程组有非零解，其同解方程组为

x₁+x₂+…+x_n=0，

于是得方程组的通解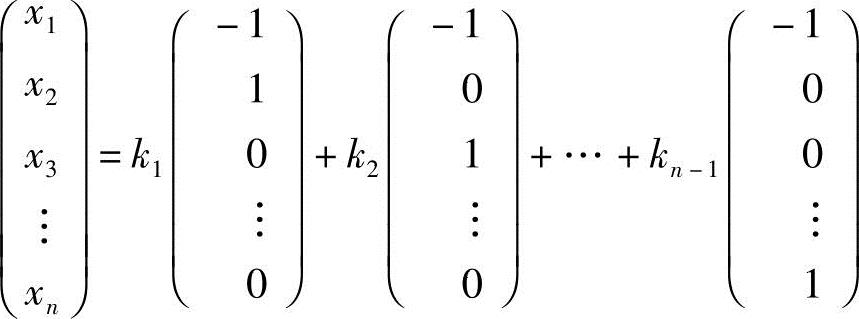，其中k₁，…，k_n-1为任意常数.

当a≠0时，对矩阵B作初等行变换，有

可知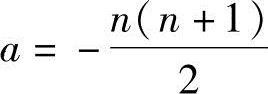时，R（A）=n-1<n，故方程组也有非零解，其同解方程组为

于是得方程组的通解

，其中k为任意常数.

例3.10 设非齐次线性方程组

求λ为何值时，此方程组：（1）有唯一解；（2）无解；（3）有无穷多解？并在有无穷多解时，求其通解.

解 因系数矩阵A为方阵，故由克拉默法则知，方程组有唯一解的充分必要条件是其系数行列式A≠0.而

所以当λ≠0且λ≠1时，方程组有唯一解.

当λ=0时，对方程组的增广矩阵作初等行变换：

因R（A）=2<R（B）=3，故方程组无解.

当λ=1时，增广矩阵为

因R（A）=R（B）=2<3，故方程组有无穷多个解.得同解的方程组

令x₃=c，得方程组的通解

注 （1）含参数的n个未知数n个方程的线性方程组，当n≤3时，通常利用系数行列式进行分析讨论：当系数行列式不为零时，方程组有唯一解，用克拉默法则求之；当系数行列式为零时，利用增广矩阵的初等行变换化为行阶梯形矩阵判别有无解，有解时进一步化为行最简形，求出通解.

（2）当方程的个数≠未知数的个数或（1）中的n>3时，通常是对方程组的增广矩阵施以初等行变换化为行阶梯形，然后再针对参数讨论方程组有无解，有无穷多解时进一步化为行最简形，求出通解.

例3.11 当p，t取何值时，线性方程组

有唯一解、无解或有无穷多解？若有解，求出所有的解.

解 对方程组的增广矩阵施以初等行变换化为行阶梯形：

（1）当p≠2时，R（A）=R（B）=4，方程组有唯一解.依次回代可解得

（2）当p=2时，有

当t≠1时，R（A）=3<R（B）=4，方程组无解；

当t=1时，R（A）=R（B）=3<4，方程组有无穷多解.此时

得同解的方程组

令x₃=c，得方程组的通解

注 对含字母的线性方程组，要对字母的所有可能情况进行分析，并全面考虑各种情况.