1.求下列矩阵的乘积:
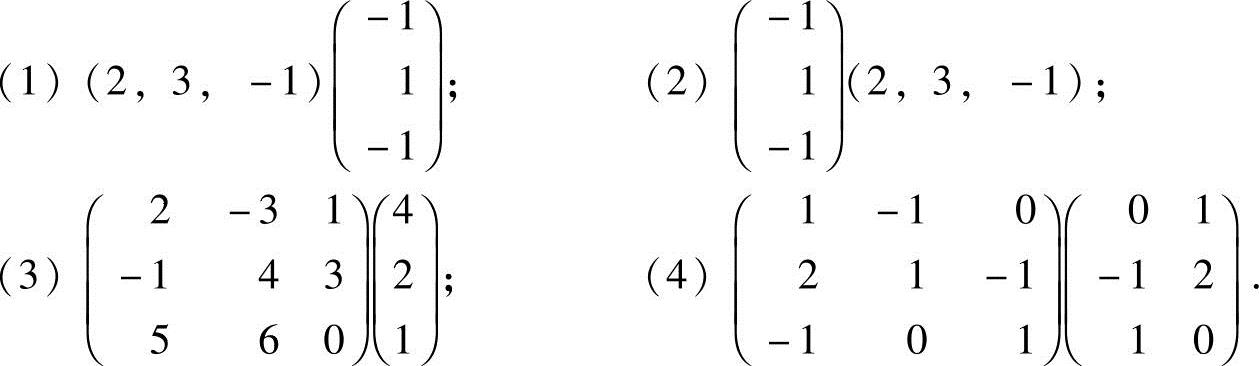
解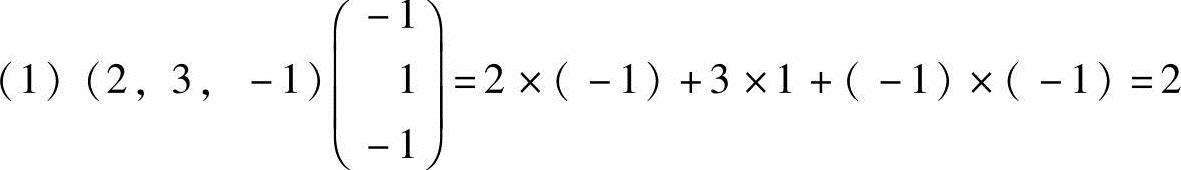 ;
;
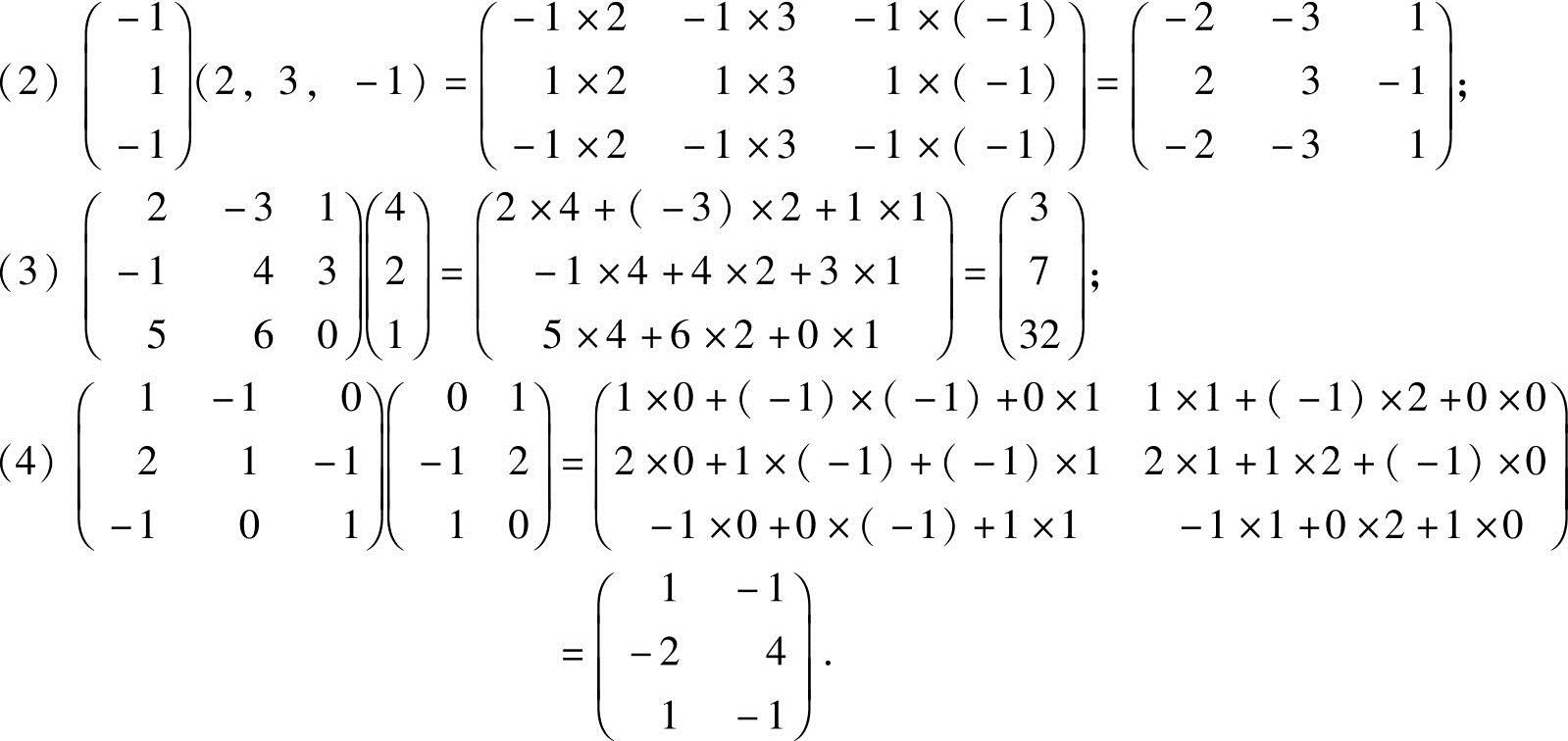
2.设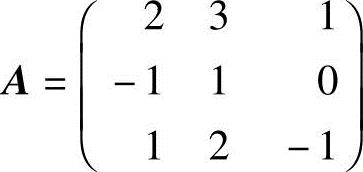 ,
,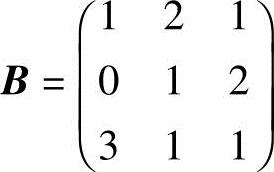 ,求:(1)2AB-A;(2)ATB.
,求:(1)2AB-A;(2)ATB.
解 (1)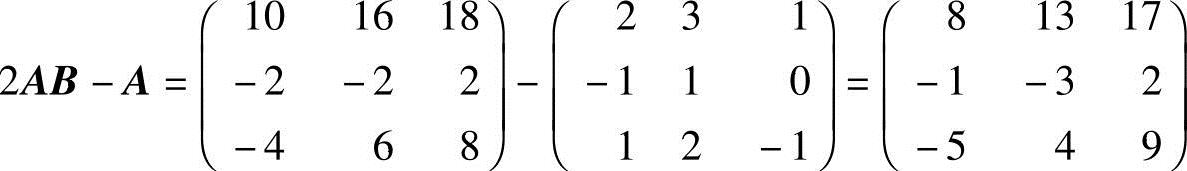 ;
;
(2) .
.
3.设甲、乙、丙、丁四人的数学、语文、外语的期中、期末考试成绩如表2-9、表2-10所示:
(1)分别写出表示甲、乙、丙、丁四人的期中、期末考试成绩的矩阵A,B;
(2)学生的学期成绩的计算方法是期中考试成绩占20%,期末考试成绩占80%,若表示甲、乙、丙、丁四人的学期成绩的矩阵为C,写出C与A,B的关系,并求出C(最后成绩中的小数四舍五入).
表2-9 期中考试成绩
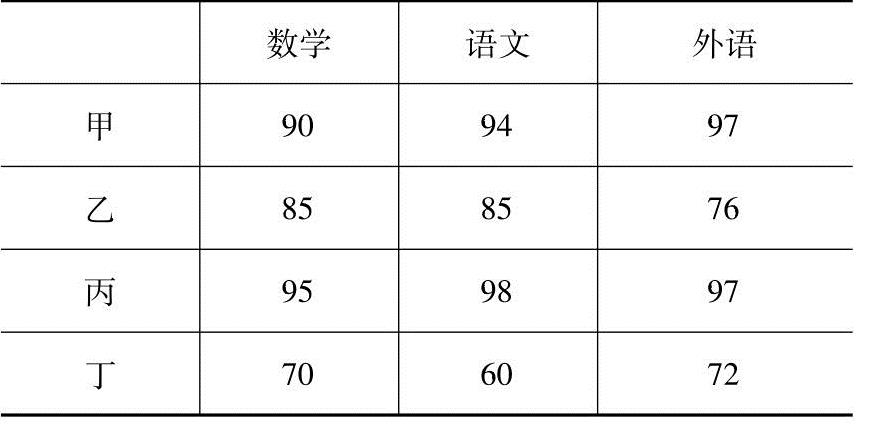
表2-10 期末考试成绩
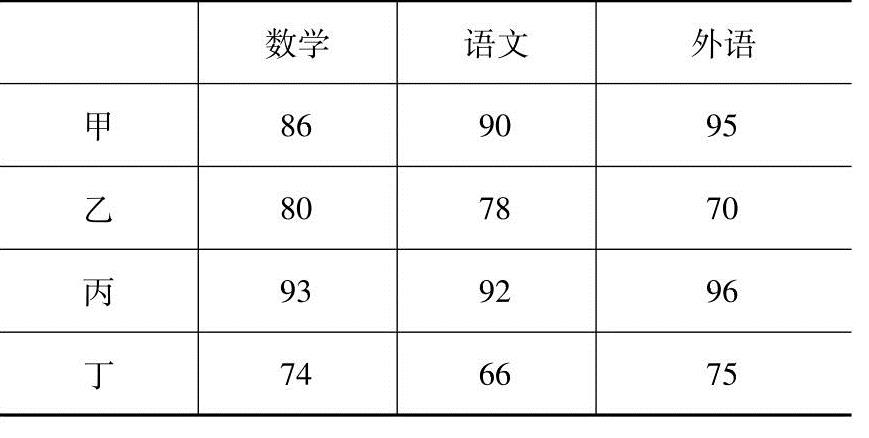
解 (1)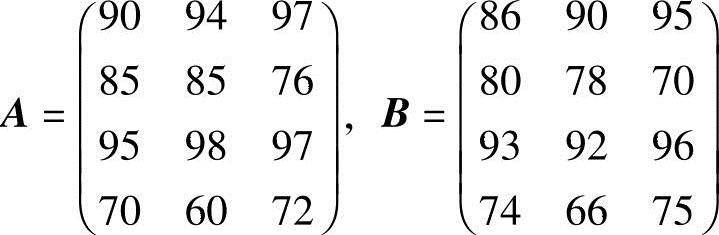 ;
;
(2)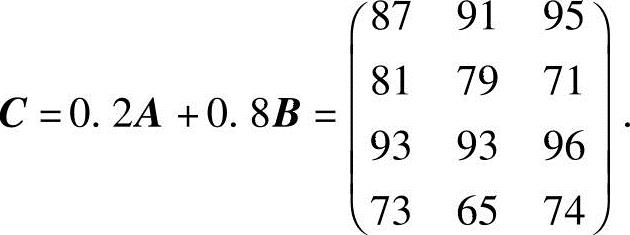
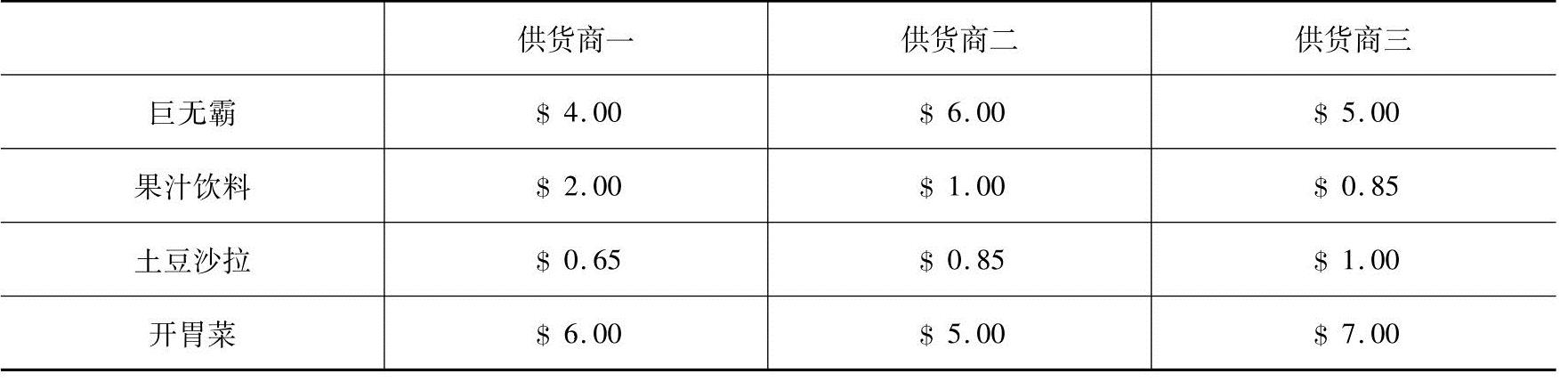
4.设一次聚会需要准备的餐饮为10个大型三明治(巨无霸)、6夸脱(每夸脱约1.14升)果汁饮料、3夸脱土豆沙拉及2盘开胃菜.统计表2-11是3家不同供货商提供这些商品的单价:
求每个供货商的备餐价格.
表 2-11
解 依照题意分别设矩阵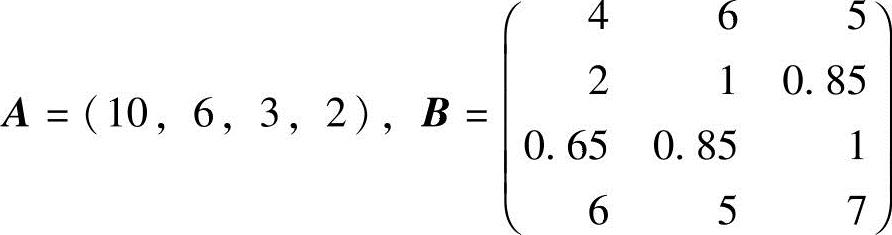 ,每个供货商的备餐价格对应矩阵C,则
,每个供货商的备餐价格对应矩阵C,则
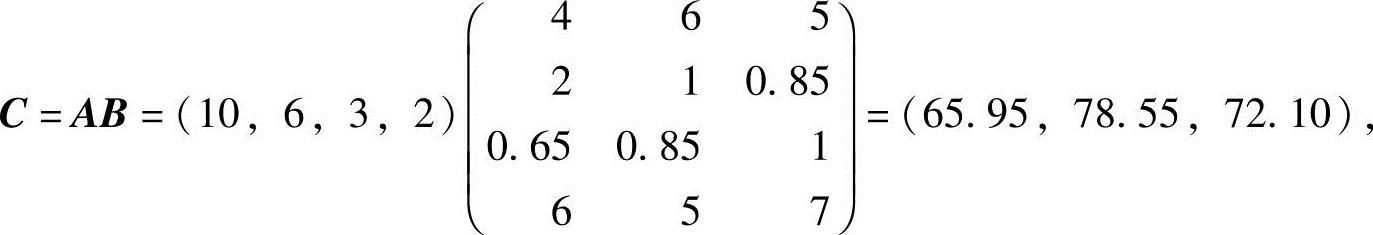
其中,c1j表示第j个供货商的备餐价格(j=1,2,3).
5.设线性变换
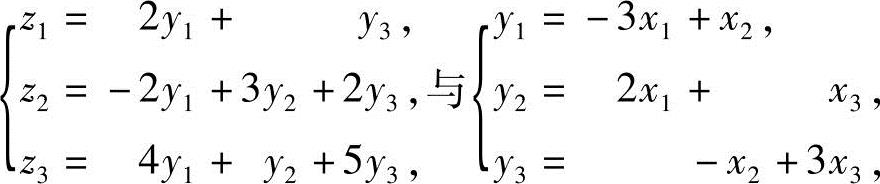
求从变量x1,x2,x3到z1,z2,z3的线性变换.
解 依次将两个线性变换写成矩阵形式:
Z=AY,Y=BX,
其中,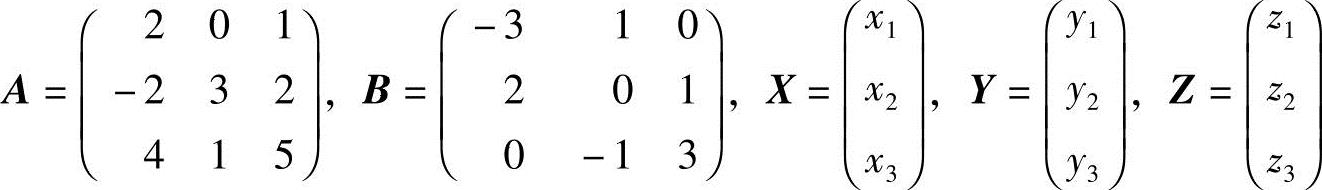 .则从变量x1,
.则从变量x1,
x2,x3到z1,z2,z3的线性变换的矩阵形式为
Z=AY=A(BX)=(AB)X,
这里矩阵
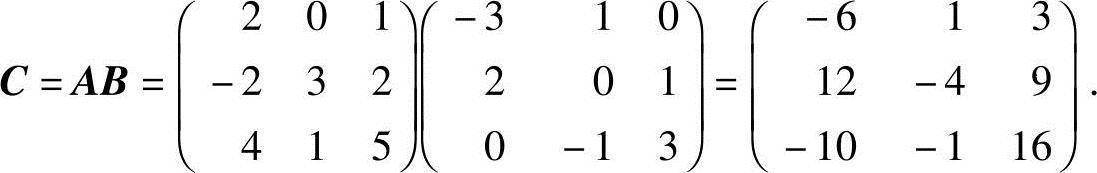
即有
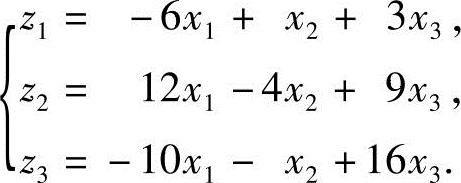
6.设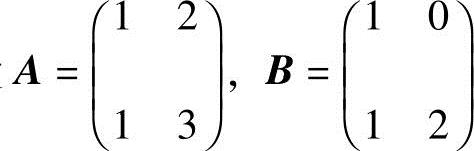 ,验证AB≠BA,并说明下列公式:
,验证AB≠BA,并说明下列公式:
(1)(A+B)2=A2+2AB+B2;
(2)(A+B)(A-B)=A2-B2是否成立.
解 因为

显然,
AB≠BA.
(1)(A+B)2=(A+B)(A+B)=A2+AB+BA+B2,由于AB≠BA,故
AB+BA≠2AB,
从而
(A+B)2≠A2+2AB+B2;
(2)(A+B)(A-B)=A2+BA-AB-B2,由于AB≠BA,故BA-AB≠O,从而
(A+B)(A-B)≠A2-B2.
7.举例说明:若A2=A,则A=O或A=E这一结论不一定成立.
解 取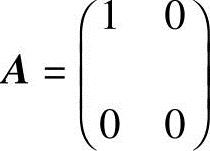 ,有A2=A,但A≠O且A≠E.
,有A2=A,但A≠O且A≠E.
8.求下列方阵的n次幂An:
(1)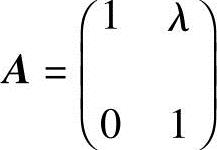 ; (2)
; (2)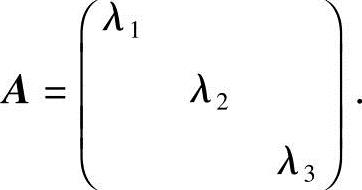
解 (1)由
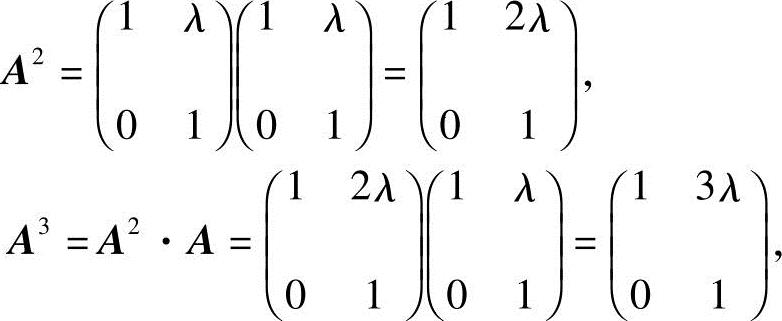
可推得

下面用数学归纳法证之.
当n=1时,式(2-1)显然成立.
假设当n=k时,式(2-1)成立.那么,当n=k+1时,
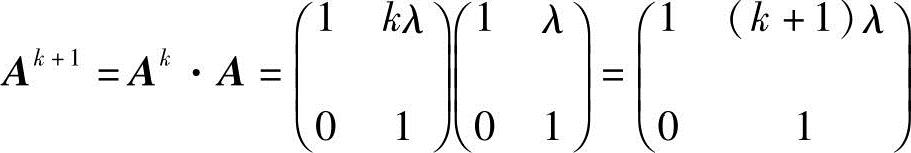
成立.故
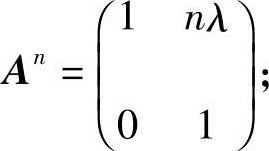
(2)由
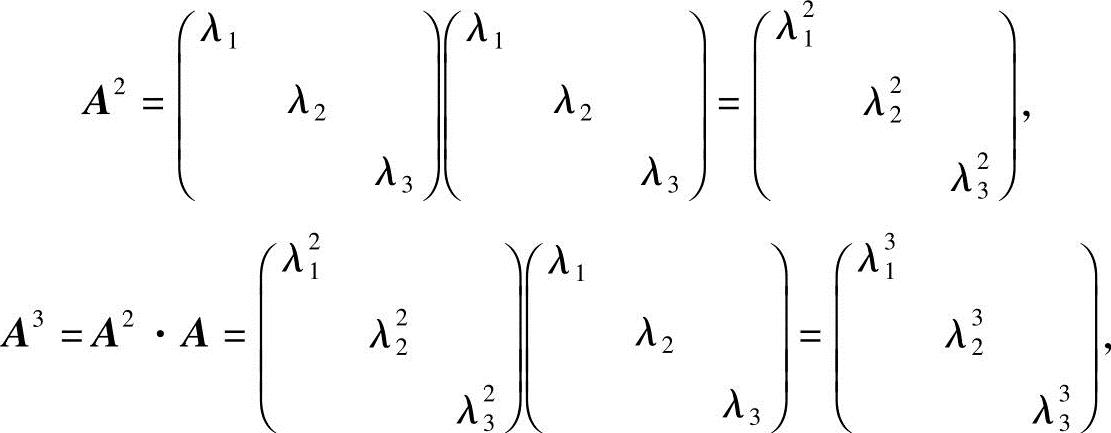
可推得

当n=1时,式(2-2)显然成立.
假设当n=k时,式(2-2)成立.那么,当n=k+1时,
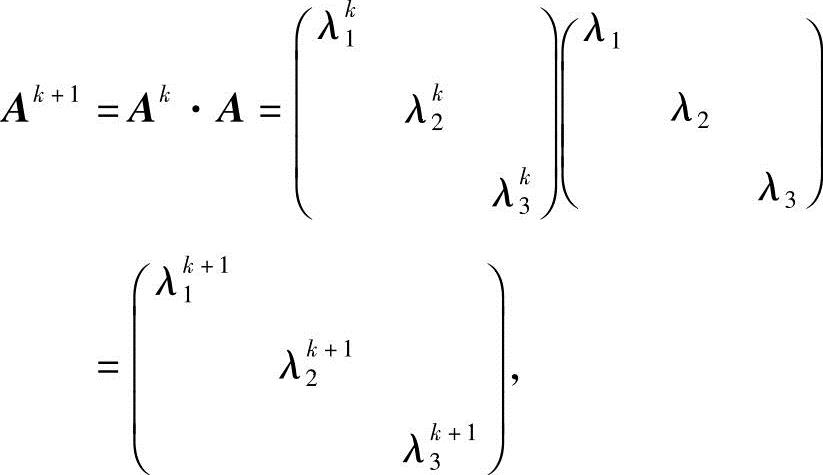
由数学归纳法知式(2-2)成立.
9.设
αT=(1,2,3),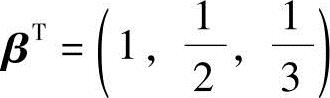 ,A=αβT,求An(n>1).
,A=αβT,求An(n>1).
解 由方阵幂的定义有
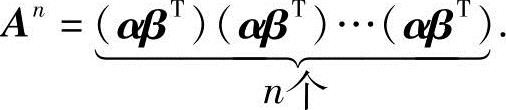
利用矩阵乘法的结合律,得
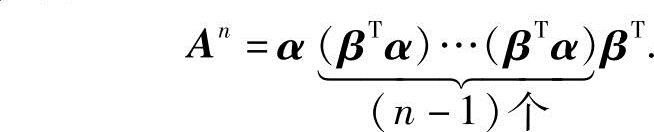
注意到βTα是一个1×1矩阵,即βTα=3,根据矩阵数乘的运算规则,有
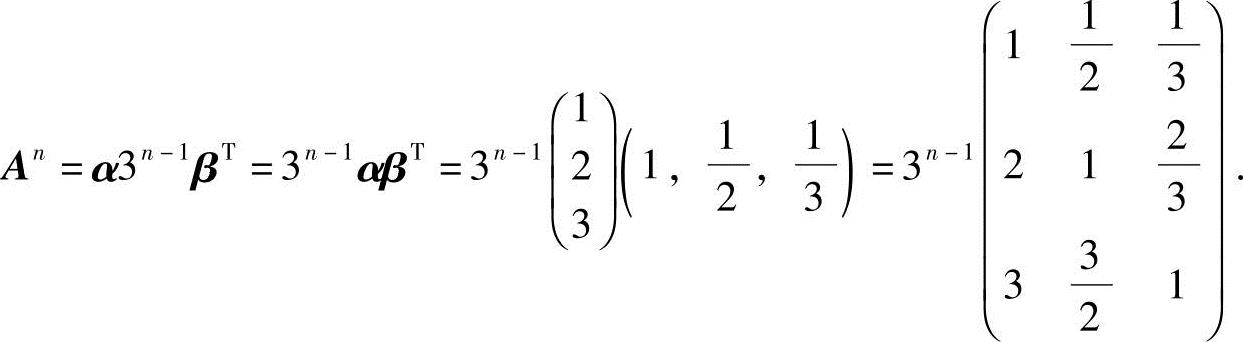
10.设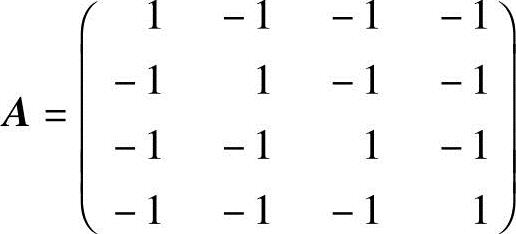 ,求A2,A3,…,An.
,求A2,A3,…,An.
解 由
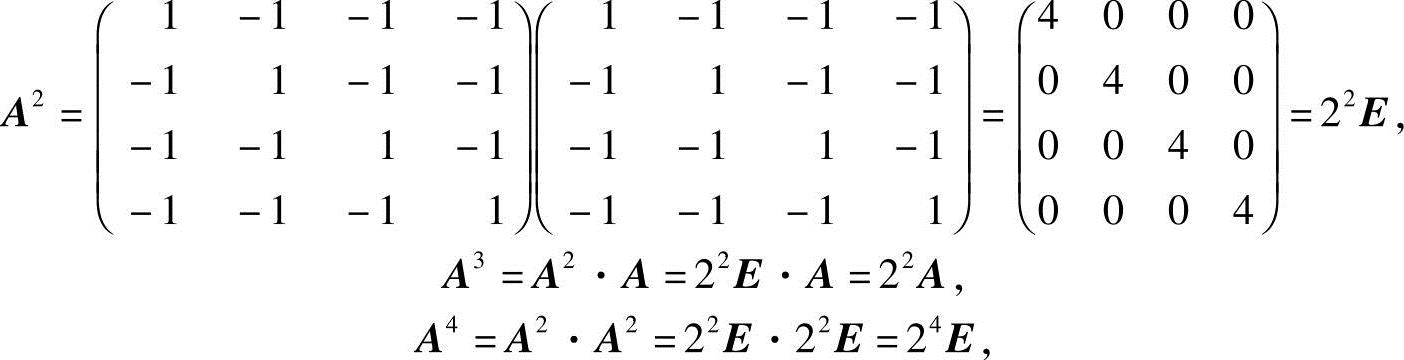
得,当n=2m时,
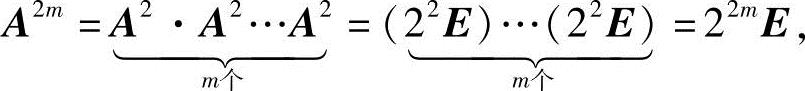
当n=2m+1时,
A2m+1=A2mA=22mE·A=22mA,
故
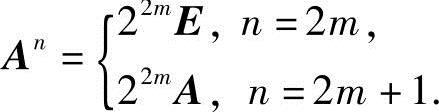
11.设A,B为n阶方阵,且A为对称阵,证明BTAB也是对称阵.
证 因为A为对称阵,由对称阵的定义得AT=A,所以
(BTAB)T=BTAT(BT)T=BTAB,
即BTAB也是对称阵.
12.设A,B是n阶对称阵,证明AB是对称阵的充分必要条件是AB=BA.
证 由A,B是对称阵,得AT=A,BT=B.
充分性.由于AB=BA,故有(AB)T=BTAT=BA=AB,因此AB是对称阵.
必要性.因为AB是对称阵,有AB=(AB)T=BTAT=BA,即得AB=BA.
13.求下列方阵的逆阵:
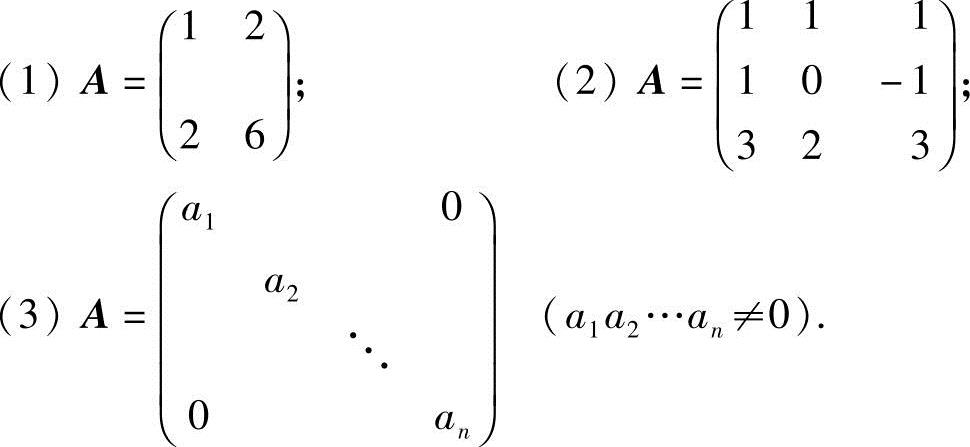
解 (1)由于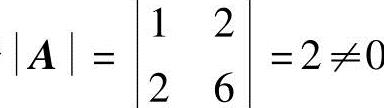 ,所以方阵A可逆.又A的伴随阵
,所以方阵A可逆.又A的伴随阵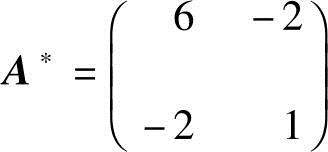 ,所以有
,所以有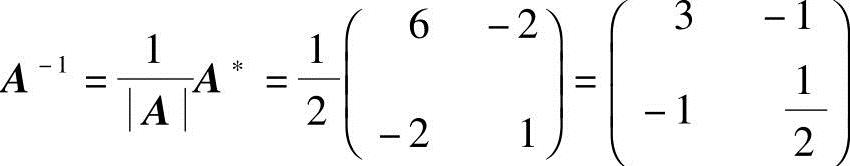 ;
;
(2)由于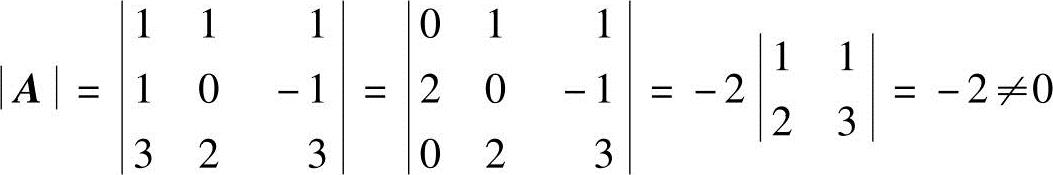 ,方阵A可逆.
,方阵A可逆.
又行列式A的元素的余子式为:
M11=2,M21=1,M31=-1,
M12=6,M22=0,M32=-2,
M13=2,M23=-1,M33=-1,
从而,A的伴随阵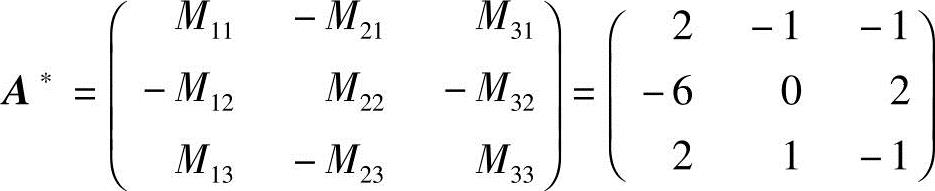 ,于是
,于是
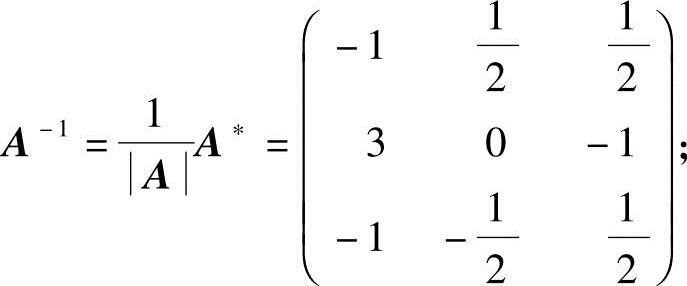
(3)因a1a2…an≠0,故ai≠0(i=1,2,…,n).于是矩阵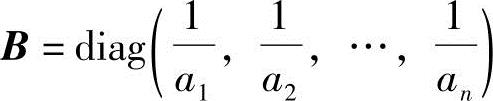 是有意义的,并且因
是有意义的,并且因
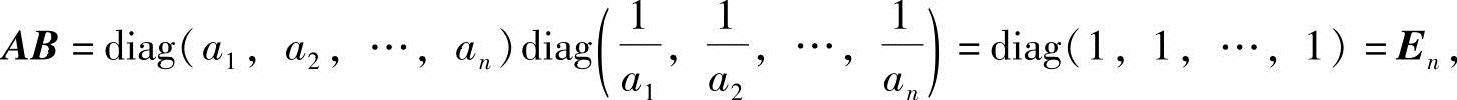
由教材中的定理2.1的推论可知A可逆,且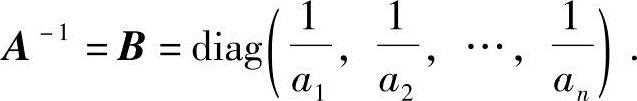
14.求解下列矩阵方程:
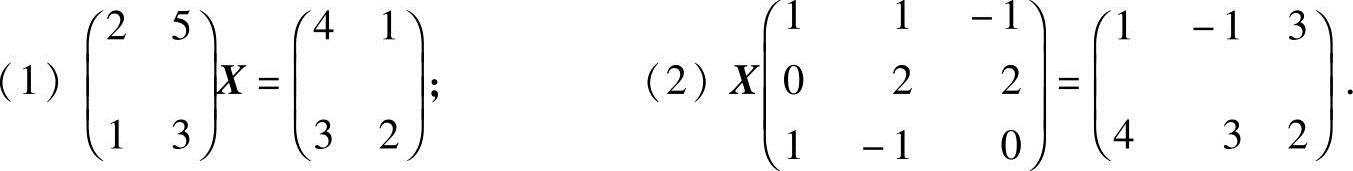
解 (1)记 ,则原矩阵方程记为
,则原矩阵方程记为
由于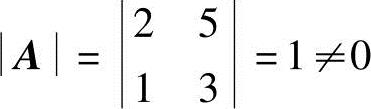
AX=B.,所以方阵A可逆.用A-1左乘等式AX=B的两边,有
A-1AX=A-1B,
即
X=A-1B.
又A的伴随阵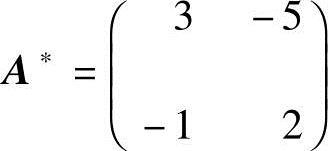 ,所以有
,所以有
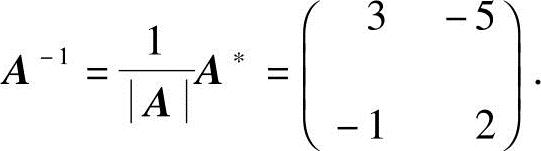
于是
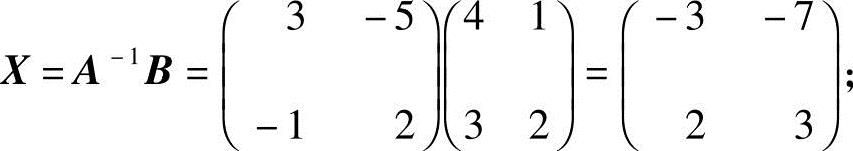
(2)记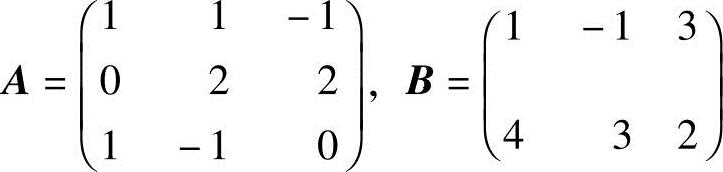 ,则原矩阵方程记为XA=B.
,则原矩阵方程记为XA=B.
由于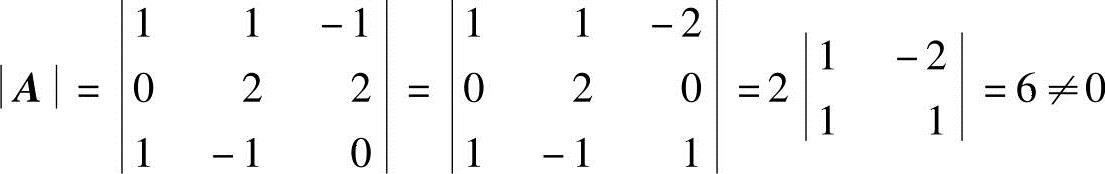 ,方阵A可逆.用A-1右乘等式XA=B的两边,有
,方阵A可逆.用A-1右乘等式XA=B的两边,有
XAA-1=BA-1,
即
X=BA-1.
又
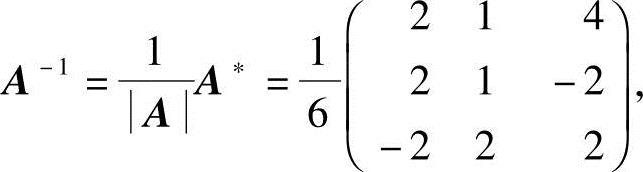
于是

15.设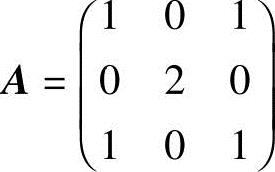 ,且AB+E=A2+B,求B.
,且AB+E=A2+B,求B.
解 由方程AB+E=A2+B,合并含有未知矩阵B的项,得
AB-B=A2-E=(A-E)(A+E),
即
(A-E)B=(A-E)(A+E),(2-3)
又
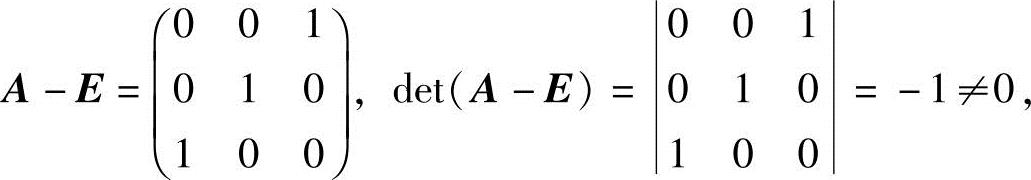
故A-E可逆,用(A-E)-1左乘式(2-3)的两边,得
(A-E)-1(A-E)B=(A-E)-1(A-E)(A+E),
即
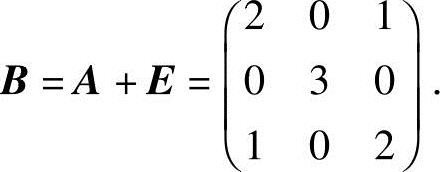
16.设方阵A的伴随阵A*=diag(1,1,1,8),且ABA-1=BA-1+3E,求B.
解 化简所给矩阵方程
ABA-1=BA-1+3E
⇒(A-E)BA-1=3E
⇒(A-E)BA-1A=3A
⇒(A-E)B=3A,
再用A-1左乘上式两边,得
A-1(A-E)B=3A-1A
⇒(E-A-1)B=3E.
由A*=AA-1,得
A*=A4A-1=A3,
而A*=8,故A=2.因此
则(https://www.xing528.com)
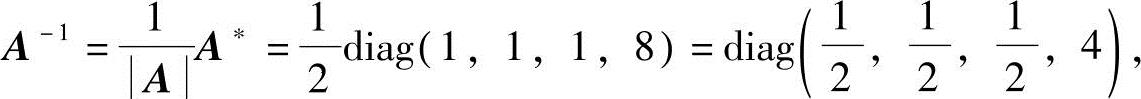
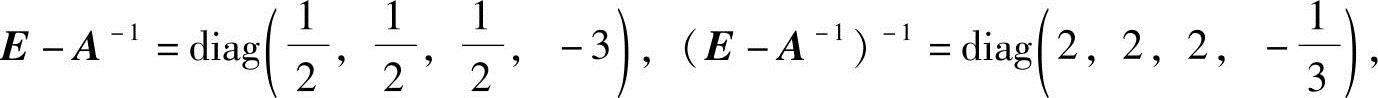
于是
B=3(E-A-1)-1=diag(6,6,6,-1).
17.利用逆阵解线性方程组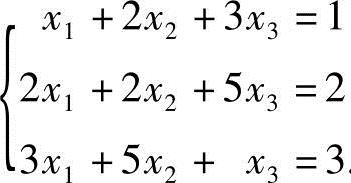 ,,.
,,.
解 记方程组的系数矩阵A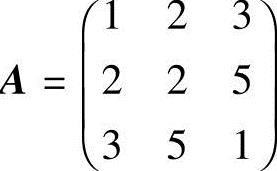 ,未知数向量
,未知数向量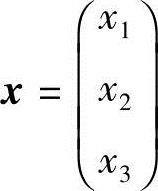 ,常数项向量
,常数项向量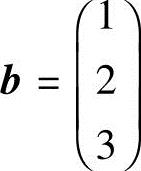 ,
,
由矩阵的乘法,该线性方程组可表示成向量方程Ax=b.
因为A=15≠0,所以方阵A可逆,从而x=A-1b.
又
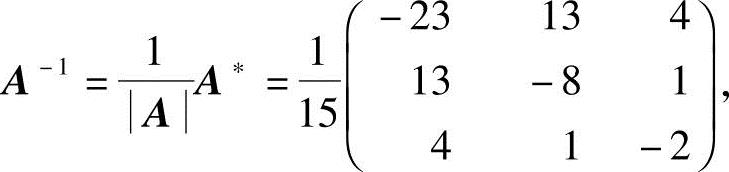
故
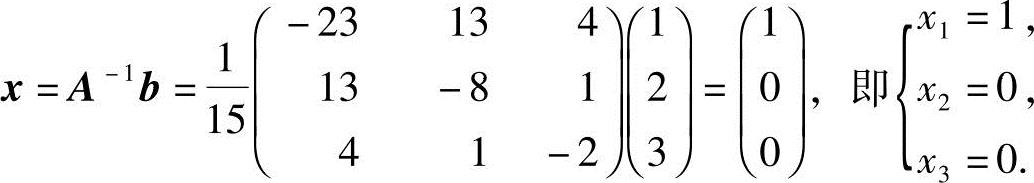
18.求线性变换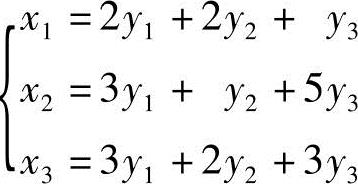
,
,的逆变换.
解 记x=(x1,x2,x3)T,y=(y1,y2,y3)T,则上述线性变换的矩阵形式为x=Ay,
其中它的系数矩阵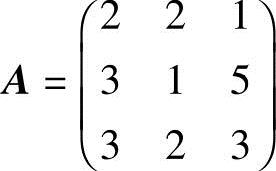 .因A=1≠0,故A是可逆阵,于是从变量x1,x2,x3
.因A=1≠0,故A是可逆阵,于是从变量x1,x2,x3
到变量y1,y2,y3的线性变换的矩阵形式为
y=A-1x.
又
于是
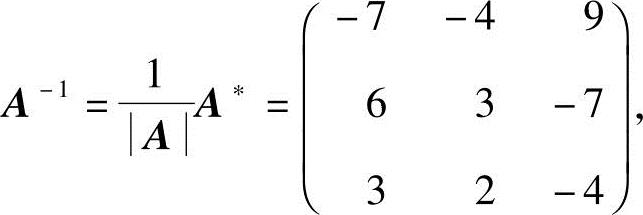
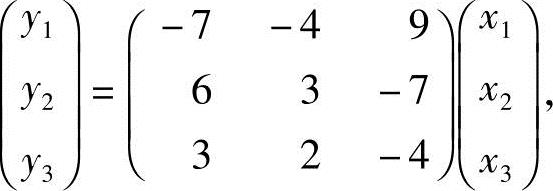
即
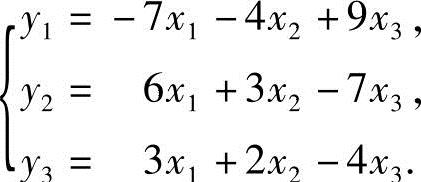
19.设A为三阶方阵,且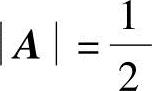 ,求(2A)-1-5A*.
,求(2A)-1-5A*.
解 因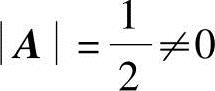 ,故A可逆.于是由
,故A可逆.于是由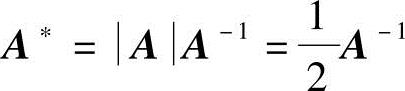
及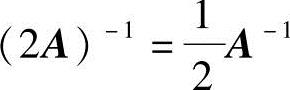 ,
,
得
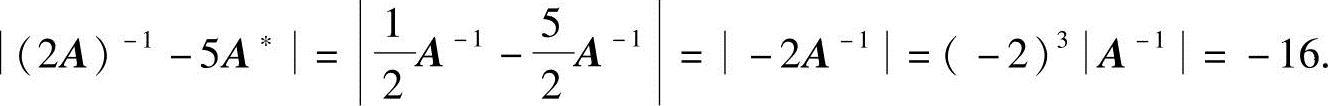
20.设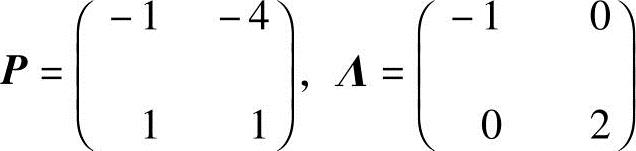 ,且AP=PΛ,求A11.
,且AP=PΛ,求A11.
解 因为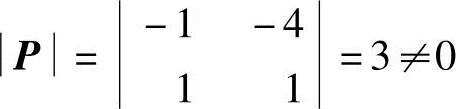 ,所以方阵P可逆.于是,
,所以方阵P可逆.于是,
A=PΛP-1,A2=PΛ(P-1P)ΛP-1=PΛ2P-1,…,A11=PΛ11P-1,
由
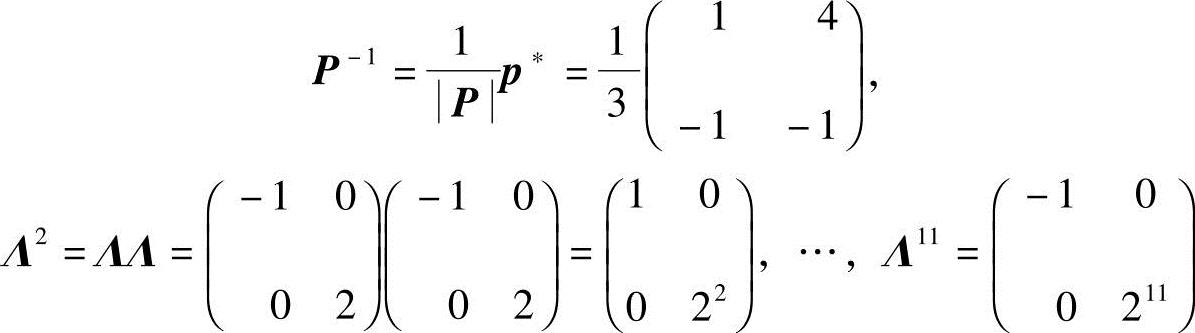
得
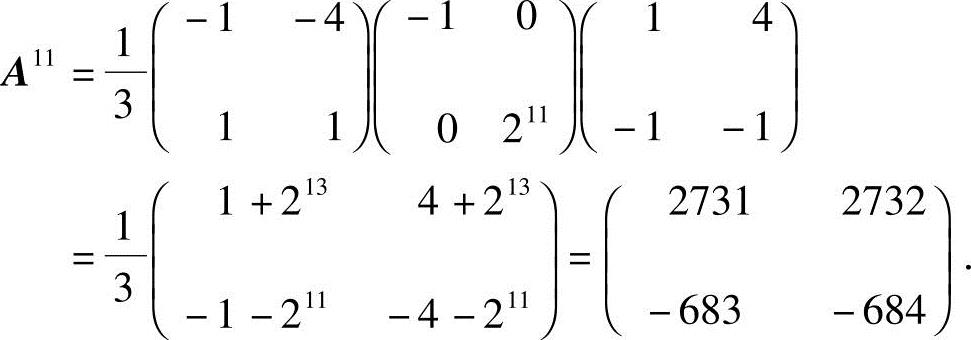
21.设方阵A满足A2+A-4E=O,证明A与A-E都可逆,并求A-1与(A-E)-1.
解 由等式A2+A-4E=O,得(A+E)A=4E,从而
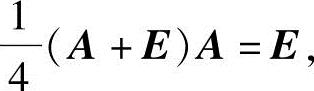
由教材中的定理2.1的推论可知方阵A可逆,且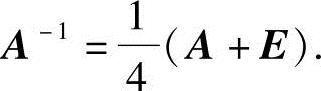
又由等式A2+A-4E=O,得(A2-A)+(2A-2E)-2E=O,从而有
A(A-E)+2(A-E)=2E,
即
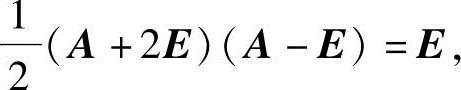
由教材中的定理2.1的推论可知方阵A-E也可逆,且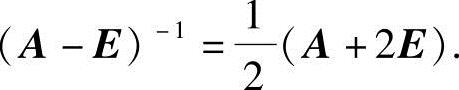
22.设方阵A可逆,证明A的伴随阵A*也可逆,且(A*)-1=(A-1)*.
证法一 因AA*=AE及A≠0,由教材中的定理2.1的推论知A*可逆,且
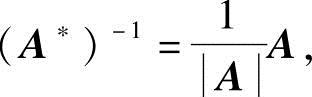
另一方面,因A-1(A-1)*=|A-1|E,用A左乘此式两边得
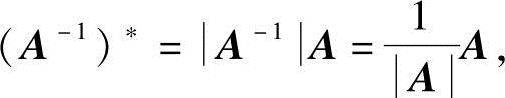
比较两个式子,即知结论成立.
证法二 由AA*=AE及A可逆,可得
A*=AA-1,
所以
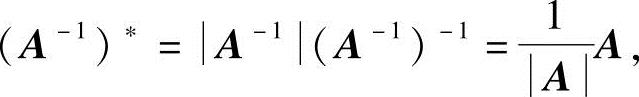
于是
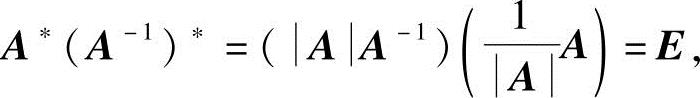
由教材中的定理2.1的推论知,A*可逆,且(A*)-1=(A-1)*.
23.设A*是n阶方阵A的伴随阵,证明:
(1)若|A|=0,则|A*|=0; (2)|A*|=|A|n-1.
证 (1)因AA*=|A|E,当A=0时,上式成为AA*=O.
欲证|A*|=0,可用反证法:假设|A*|≠0,由矩阵可逆的充要条件知,A*是可逆矩阵,用(A*)-1右乘上式等号两边,得A=O.从而得A的伴随矩阵|A*|=O,于是|A*|=0,这与假设矛盾,所以假设不成立,而原结论即|A*|=0成立.
(2)当|A|=0时.由(1)问可知,|A*|=0=An-1,结论成立;
当|A|≠0时.在等式A|A*|=|A|E的两边取行列式,得
A|A*|=A|A*|=||A|En=|An|,
于是
|A*|=|An-1|.
24.在用可逆阵进行保密编译码中(教材中的例2.19),取可逆阵为
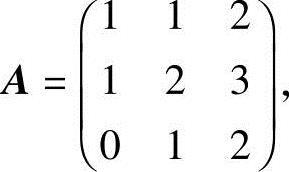
若发出信息school,问收到的信息是什么?若收到信息为43,64,41,42,59,22,恢复原来的信息是什么?
解 使用代码:将26个英文字母a,b,…,y,z依次对应数字1,2,…,25,26.若发送信息是school,此信息的编码是19,3,8,15,15,12.将编码19,3,8,15,15,12写成两个传出信息向量(19,3,8)T,(15,15,12)T.
因为

所以将传出信息向量经过乘A编成“密码”后发出,收到信息为38,49,19,54,81,39.
又因为

所以,将所收到的两个信息写成向量后,经过乘A-1给予解码为2,1,20,20,12,5.
最后,利用使用的代码将编码恢复为明码,得到信息battle.
25.设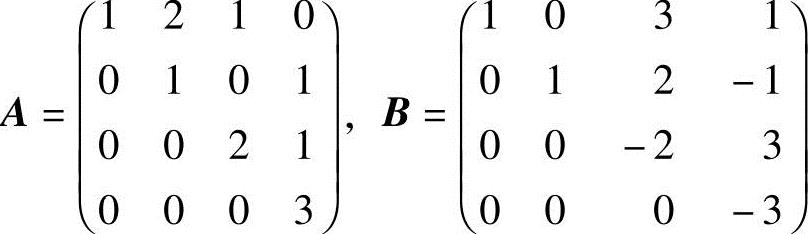 ,求AB.
,求AB.
解 记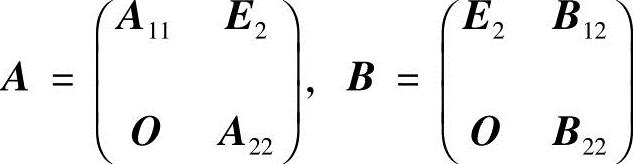 ,其中
,其中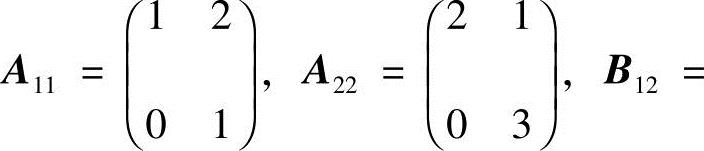
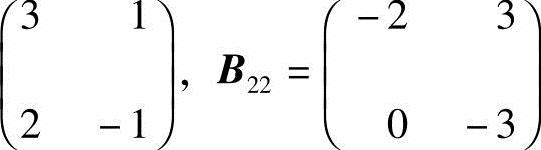 .则
.则
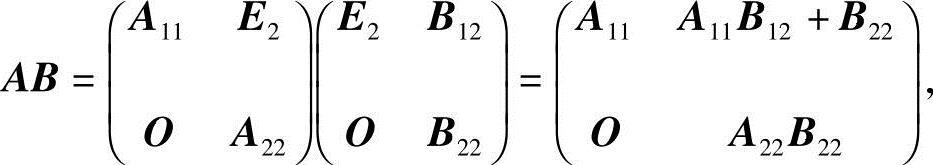
又
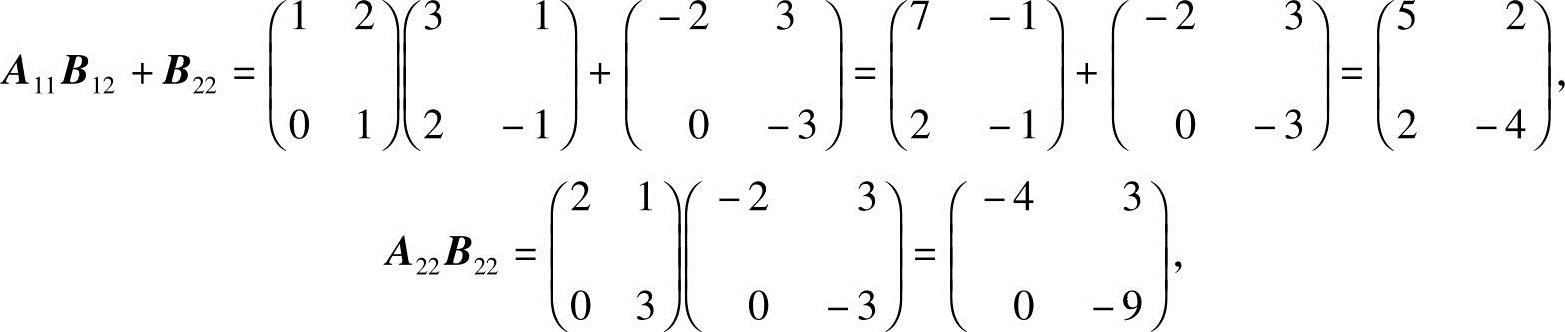
故

26.设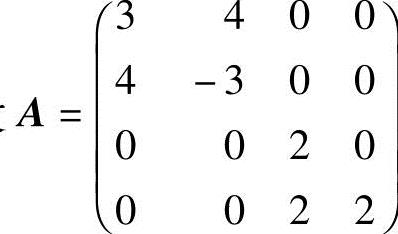 ,求:(1)A8;(2)A-1;(3)A4.
,求:(1)A8;(2)A-1;(3)A4.
解 记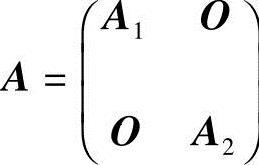 ,其中,
,其中,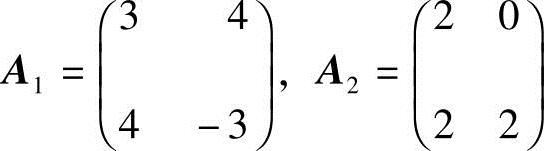 ,则A成为一个分块对角矩阵.
,则A成为一个分块对角矩阵.
(1)A8=A8=(A1A2)8=A18A28=1016;
(2)由于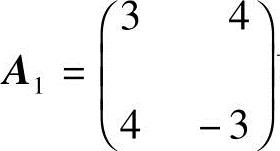 可逆,
可逆,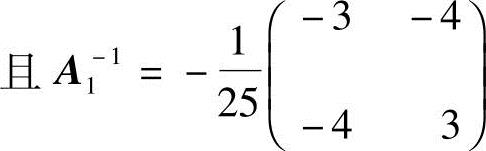 ;
;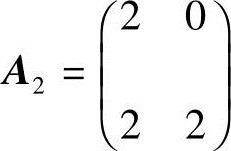 也可逆,且A2-1
也可逆,且A2-1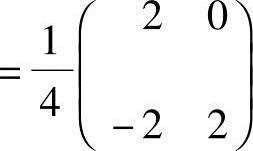 ,所以A可逆,且
,所以A可逆,且
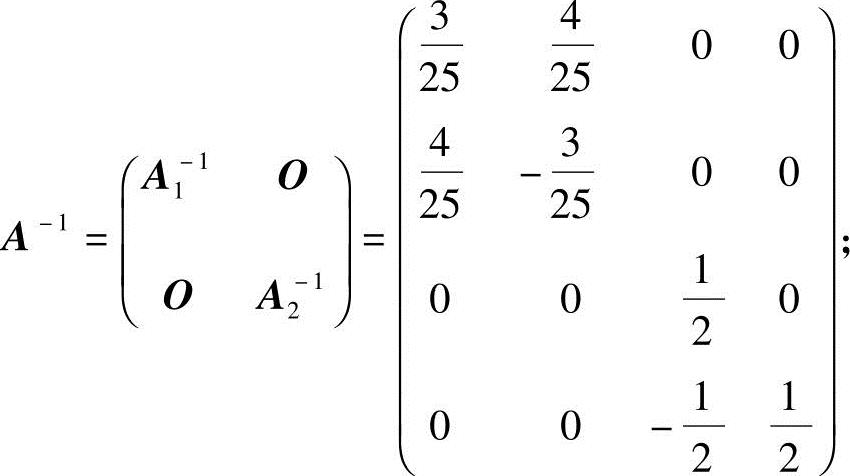
(3)计算可得
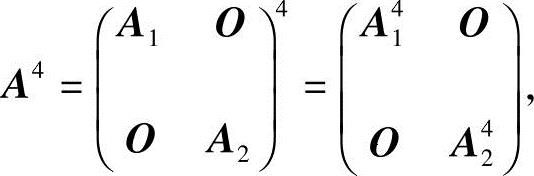
因
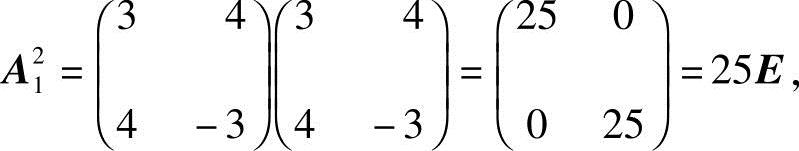
故
A41=54E,
又因
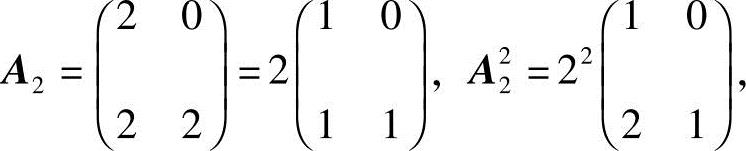
故
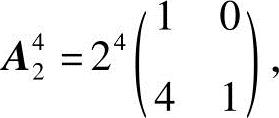
代入即得
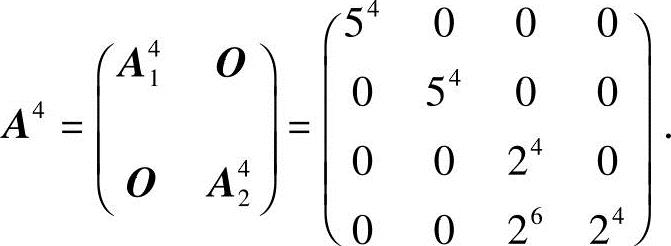
27.设方阵A,B都可逆,证明:
(1)分块阵 可逆,且
可逆,且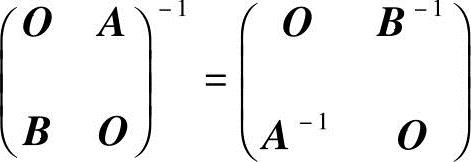 ;
;
(2)分块阵
可逆,且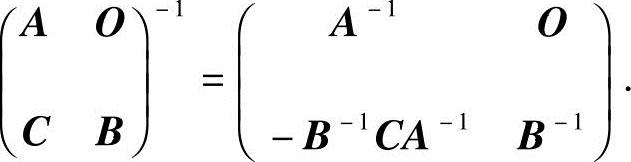
证 (1)由于A,B都可逆,故AA-1=E,BB-1=E,且有
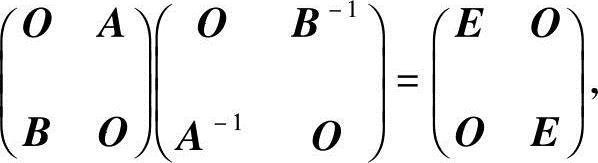
由教材中的定理2.1的推论可知分块阵
可逆,且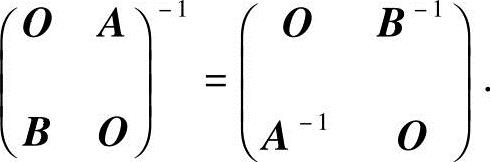
(2)由于
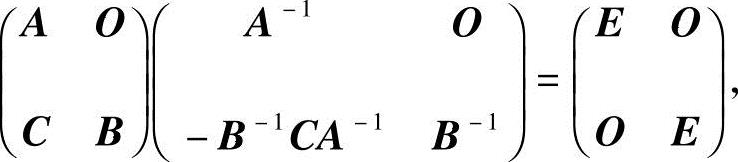
由教材中的定理2.1推论可知分块阵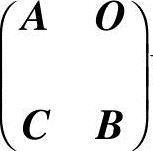
可逆,且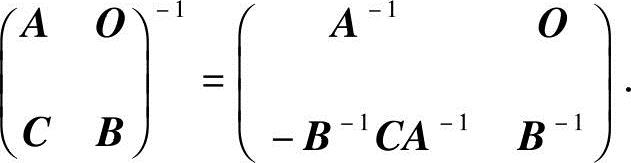
28.求下列方阵的逆阵:

解 (1)记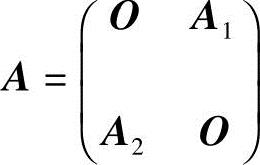 ,其中,
,其中,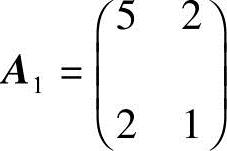 ,
,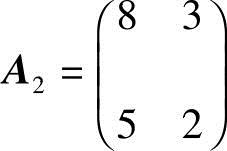 ,由第27题结论(1)有
,由第27题结论(1)有
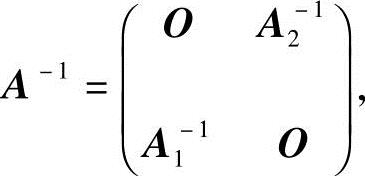
而
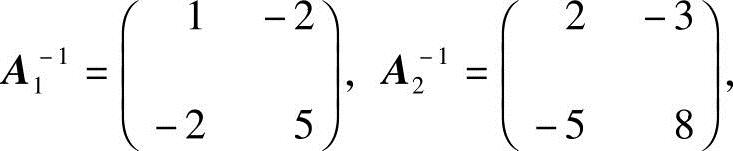
所以
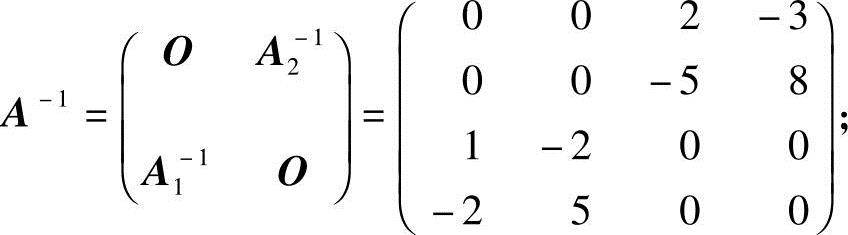
(2)记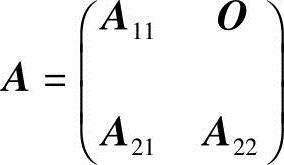 ,其中,
,其中,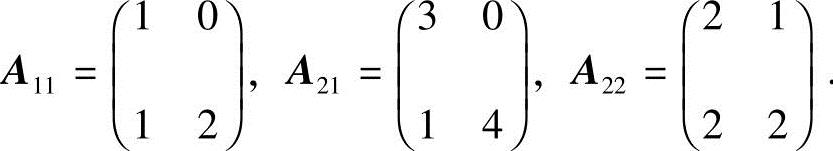 由第27题
由第27题
结论(2)有
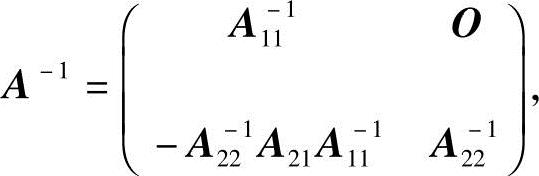
而
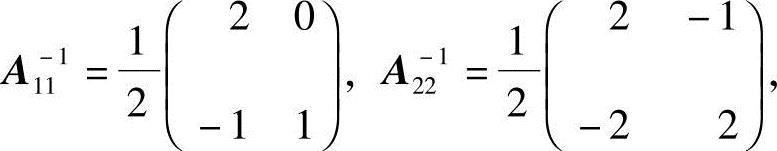
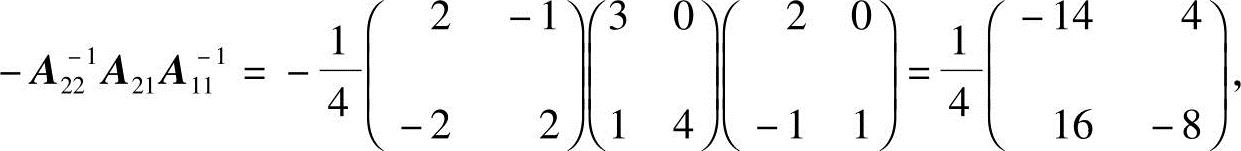
所以
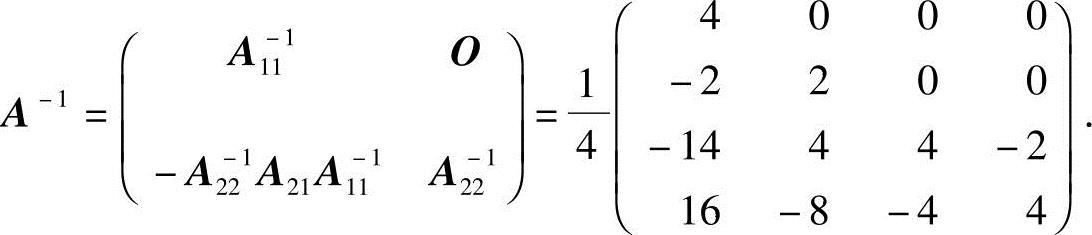
实验2
1.设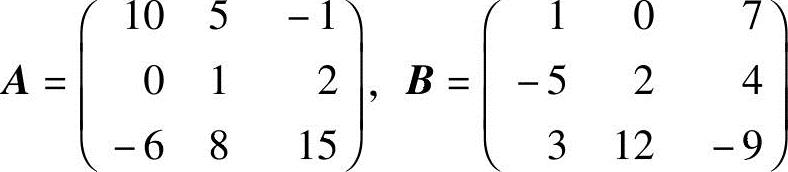 ,求AT,A+B,AB,A2,A-1B.
,求AT,A+B,AB,A2,A-1B.
解 程序设计如下:
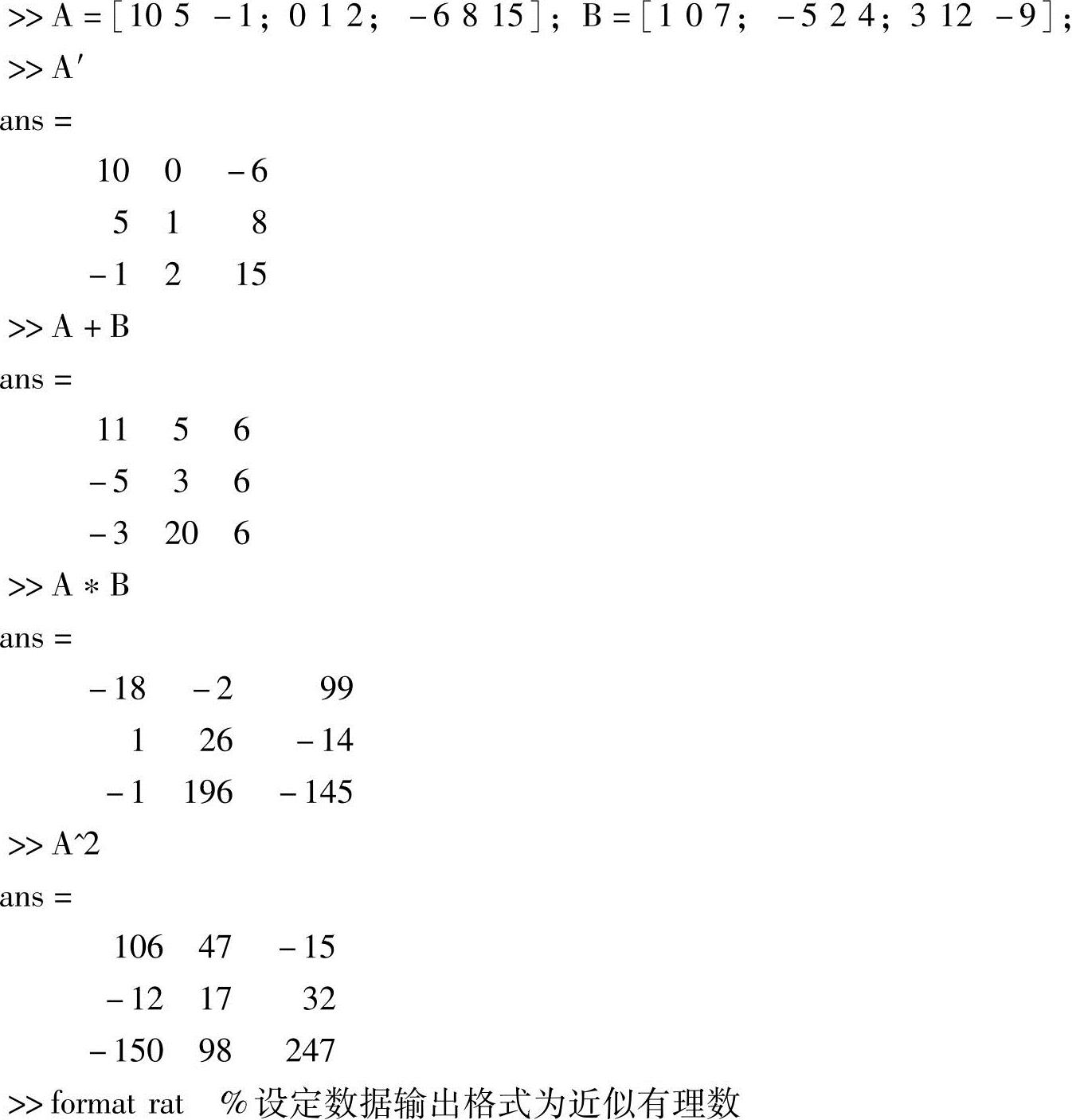

2.小李给小张发来一封密信,它是一个三阶方阵 .他们商定:消息的每一个英文字母都用一个整数来表示:a—1,b—2,…,y—25,z—26,约定好的加密矩阵是
.他们商定:消息的每一个英文字母都用一个整数来表示:a—1,b—2,…,y—25,z—26,约定好的加密矩阵是 ,现在,你知道小李说的是什么吗?
,现在,你知道小李说的是什么吗?
解 程序设计如下:
>>A=[4 3 7;9 0 10;0 7 6];B=[207 210 135;231 318 135;244 161 175];
>>formatrat
>>inv(A)*B
ans=
9 12 15
22 5 25
15 21 *故小李说的是iloveyou.
注 输出格式为近似有理数(formatrat)输出时,如果数据接近0,如0.0000之类的数会显示为*,如果调整为其他显示格式,则显示为0.0000之类的结果.
>>A=[4 3 7;9 0 10;0 7 6];B=[207 210 135;231 318 135;244 161 175];
>>=inv(A)*B
ans=
9.0000 12.0000 15.0000
22.0000 5.0000 25.0000
15.0000 21.0000 -0.0000
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




