1.填空题
(1)设矩阵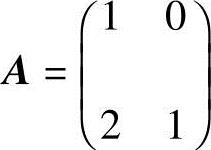 ,则与A乘积可交换的矩阵B=.
,则与A乘积可交换的矩阵B=.
(2)设A为三阶方阵,且A=2,则A*-(2A)-1=.
(3)设三阶方阵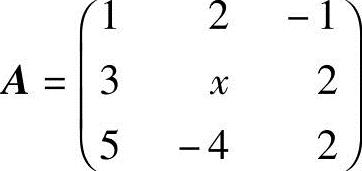 是不可逆矩阵,则x=.
是不可逆矩阵,则x=.
(4)设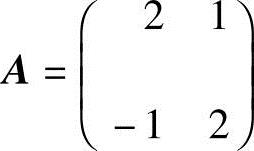 ,E为二阶单位矩阵,矩阵B满足BA=B+2E,则B=.(2006年,考研,数学一)
,E为二阶单位矩阵,矩阵B满足BA=B+2E,则B=.(2006年,考研,数学一)
(5)设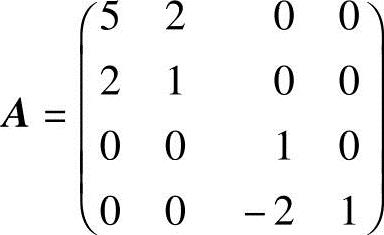 ,则A-1=.
,则A-1=.
2.单项选择题
(1)设A为非零n阶矩阵,则下列矩阵中不是对称矩阵的是( ).
(A)AAT; (B)ATA;
(C)A-AT; (D)A+AT.
(2)设A,B,C均为n阶矩阵,则下列结论中错误的是( ).
(A)E-A2=(E-A)(E+A); (B)如果A2=B2,则A=B或A=-B;
(C)(AB)k=AkBk; (D)AT+BT=A+B.
(3)设A,B,C均为n阶矩阵,且ABC=E,则下列各式中总是成立的是( ).(1991年,考研,数学一)
(A)ACB=E; (B)CBA=E;
(C)BAC=E; (D)BCA=E.
(4)设A,B,C均为n阶矩阵,若有AB=AC,能推出B=C,则A应满足( ).
(A)A≠O; (B)A=O;
(C)A≠0; (D)A=0.
(5)设A为n阶非奇异方阵,A*是A的伴随矩阵,则A*=( ).(1990年,考研)(https://www.xing528.com)
(A)A; (B)An-1;
(C)An; (D)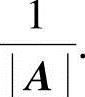
3.设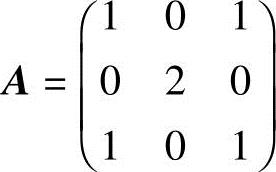 ,而n≥2为整数,求An-2An-1.
,而n≥2为整数,求An-2An-1.
4.设A,B,C均为n阶矩阵,满足等式AB=BC=CA=E,求A2+B2+C2.
5.设n阶矩阵A,B满足A+B=AB,(1)证明A-E为可逆矩阵;(2)已知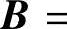
 ,求矩阵A.(1991年,考研)
,求矩阵A.(1991年,考研)
6.设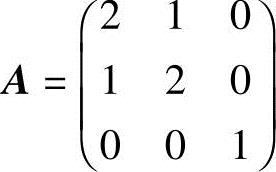 ,矩阵B满足ABA*=2BA*+E,求B.
,矩阵B满足ABA*=2BA*+E,求B.
7.设方阵A满足A2-3A-10E=O,证明A与A-4E都可逆,并求A-1与(A-4E)-1.
8.设A,B是n阶方阵,如果AB=A+2B,问A-2E是否可逆,若可逆,则求出
其逆.
参考答案
1.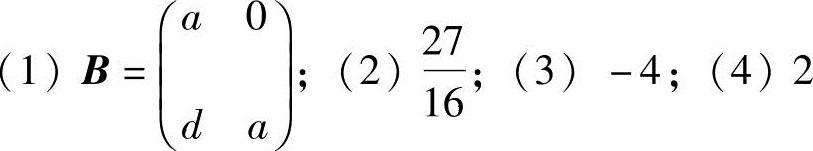 ;(5)
;(5)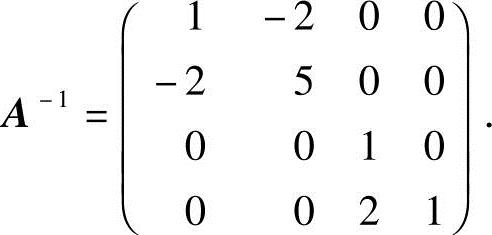
2.(1)C;(2)B;(3)D;(4)C;(5)B.
3.O.
4.3E.
5.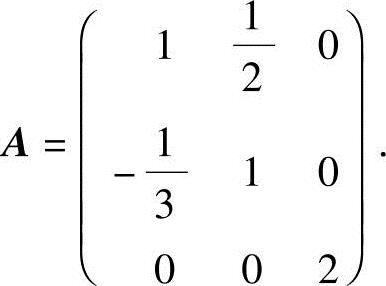
6.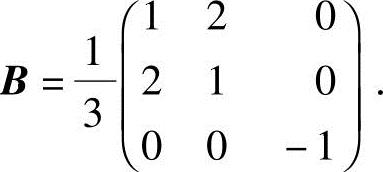
7.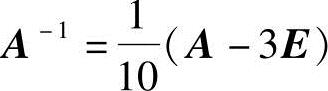 ,
,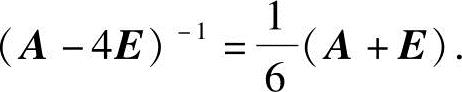
8.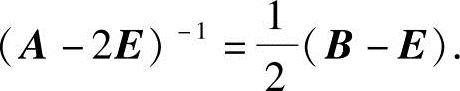
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




