线性代数学习辅导：典型例题解析

例2.1 设矩阵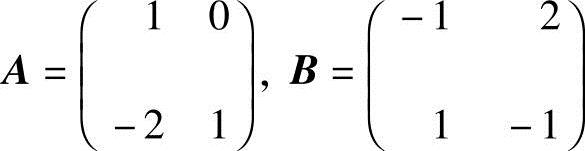，求A²-4B²+2AB-2BA.

解 先将上式化简再计算，得

A²-4B²+2AB-2BA=（A²+2AB）-2（BA+2B²）

=A（A+2B）-2B（A+2B）

=（A-2B）（A+2B），

又

故

例2.2 设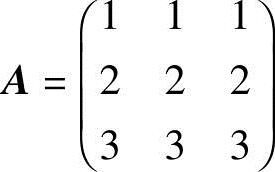，求A²，A⁴，A100.

解 由于

记

Q=（1，1，1），而QP=6，

故

注 在矩阵运算中巧妙地使用结合律，能使计算简化.例2.3 设α是三维列向量，若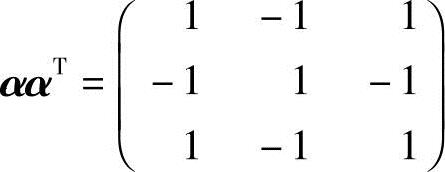，求α^Tα.

解 设α^T=（x，y，z），则

由此可得

x²=y²=z²=1，

则

注 由此题的计算，若αα^T=O，则可得到x²=y²=z²=0，即x=y=z=0，也就是说α是零向量，此结论可推广到n维向量.

例2.4 证明：对任意m×n矩阵A，A^TA及AA^T都是对称矩阵.

证 由于A是m×n矩阵，故根据矩阵的乘法可得，A^TA及AA^T分别是n阶和m阶方阵，又

（A^TA）T=A^T（A^T）T=A^TA，

（AA^T）T=（A^T）TA^T=AA^T，

根据对称矩阵的定义，A^TA及AA^T都是对称矩阵.

例2.5 当a为何值时，矩阵A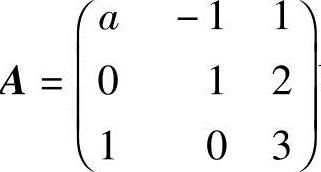可逆，并在可逆时，求A-1.

解 由于

因此，当A≠0时，即a≠1时，矩阵A可逆.

又行列式A的元素的余子式为：

M₁₁=3，M₂₁=-3，M₃₁=-3，

M₁₂=-2，M₂₂=3a-1，M₃₂=2a，

M₁₃=-1，M₂₃=1，M₃₃=a，

从而，A的伴随阵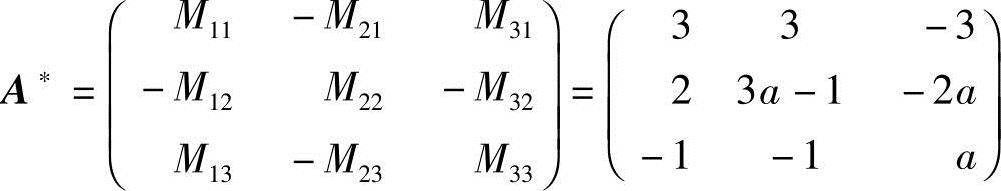（其中，a≠1），

于是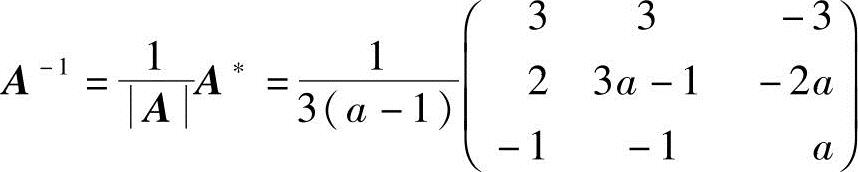（其中，a≠1）.

例2.6 设，求A¹⁰及A-1.

解 记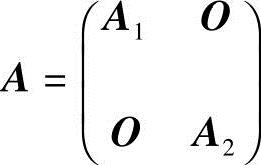，其中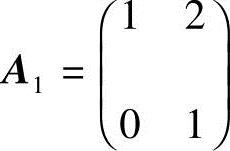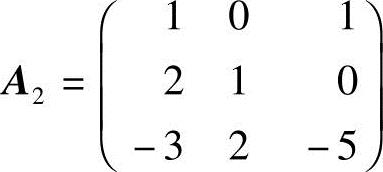，，，则A成为一个分块对角矩阵.

A¹⁰=A¹⁰=（A₁A₂）10=A₁¹⁰A₂¹⁰=2¹⁰.

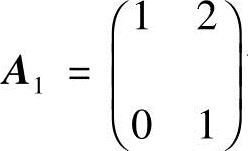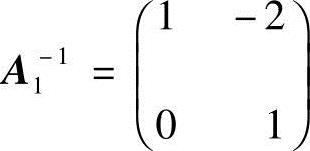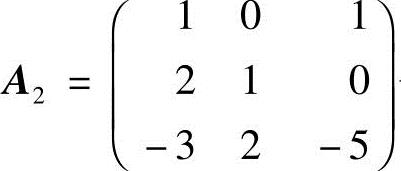由于可逆，且；也可逆，且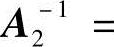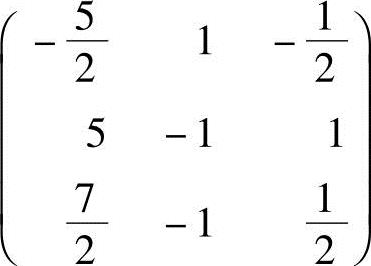，所以A可逆，且

例2.7 已知AP=PB，又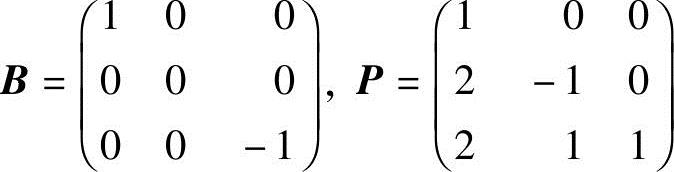，试计算A及A⁵.（1988年，考研，数学一）

解 因为

所以P可逆，于是由AP=PB得

A=PBP^-1，

又

故

又

A⁵=（PBP^-1）5=（PBP^-1）（PBP^-1）（PBP^-1）（PBP^-1）（PBP^-1）

=PB（P^-1P）B（P^-1P）B（P^-1P）B（P^-1P）BP^-1

=PB⁵P^-1.

由于B是对角阵，所以

故

A⁵=PB⁵P^-1=PBP^-1=A.

例2.8 设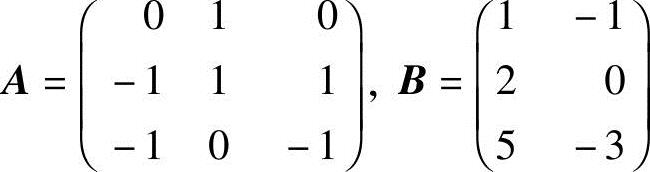，求矩阵X，使AX+B=X.

解 由AX+B=X，得AX-X=-B，即（A-E）X=-B，因为

故A-E可逆，用（A-E）-1左乘（A-E）X=-B，得

（A-E）-1（A-E）X=-（A-E）-1B，

又

故

例2.9 设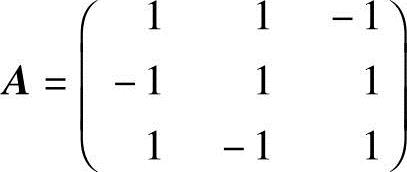，已知矩阵B满足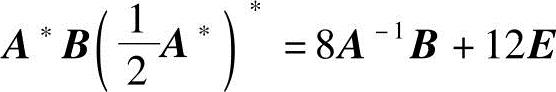，求矩阵B.

解 先将等式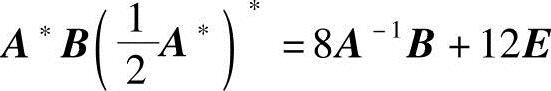化简.

因为A=4，于是A*=AA^-1=4A^-1，又因为

将此代入矩阵方程，得

A*BA=8A^-1B+12E，(www.xing528.com)

用矩阵A左乘此方程，得

AA*BA=8AA^-1B+12A，

即

4BA=8B+12A，

变形为

B（A-2E）=3A，

由于A-2E=-4，故A-2E可逆，且

于是

例2.10 设A，B，A+B都是可逆阵，求证：A^-1+B^-1也是可逆阵，并求它的逆矩阵.

证 因为

A^-1_+B-1=A^-1BB^-1+A^-1AB-1=A-1（B+A）B^-1，

又A，B，A+B都可逆，故

[A^-1（B+A）B^-1][B（B+A）-1A]=E，

因此A^-1+B^-1是可逆阵，且（A^-1+B^-1）-1=B（B+A）-1_A.

例2.11 设A，B都是n阶方阵，B是可逆矩阵，且满足A²+AB+B²=O，证明：A和A+B均可逆.

证 由

A²+AB+B²=O，

得

A（A+B）=-B²，

两边取行列式得

AA+B=-B²=（-1）nB²，

由于B可逆，则B≠0，所以A≠0，A+B≠0，

即A和A+B均可逆.

例2.12 设A为三阶方阵，且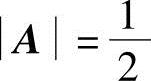，求（3A）-1-2A*.

解 因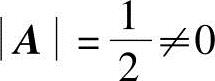，故A可逆.于是由

得

例2.13 设4阶矩阵A=（α，γ₂，γ₃，γ₄），B=（β，γ₂，γ₃，γ₄），其中α，β，γ₂，γ₃，γ₄均为4维列向量，且已知A=4，B=1，试求A+B.

解 先求两个矩阵之和，得

A+B=（α+β，γ₂+γ₂，γ₃+γ₃，γ₄+γ₄）

=（α+β，2γ₂，2γ₃，2γ₄），

则

A+B=α+β，2γ₂，2γ₃，2γ₄，

因A+B中，有公因式2的列是2，3，4列共3列，故可提取3个公因式2，得到

A+B=2³α+β，γ₂，γ₃，γ₄，

又因行列式中有一列为两分列之和，故可拆分为两行列式之和，即

A+B=8（α，γ₂，γ₃，γ₄+β，γ₂，γ₃，γ4）=8（A+B）=40.

例2.14 设A，B均为二阶矩阵，A*，B*分别为A，B的伴随矩阵，若A=2，B=

3，求分块矩阵的伴随矩阵.

解 记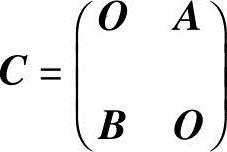.由于A=2，B=3，故A，B均可逆，且

而

从而C可逆，且

因为

C*=CC^-1，

所以

例2.15 设A=E-αα^T，其中，E为n阶单位矩阵，α是n维非零列向量，证明：

（1）A²=A的充要条件是α^Tα=1.

（2）当α^Tα=1时，A是不可逆矩阵.（1996年，考研，数学一）

证 （1）由于

A²=（E-αα^T）（E-αα^T）

=E-αα^T+（αα^T）（αα^T）-αα^T

=A+α（α^Tα）α^T-αα^T，

注意到α^Tα是一个数，记为λ，则

A²=A+λαα^T-αα^T=A+（λ-1）αα^T，

故

A²=A⇔（λ-1）αα^T=O，

又α≠0，故αα^T为非零矩阵，因此

A²=A⇔（λ-1）=0⇔λ=α^Tα=1.

（2）反证法：若A是可逆矩阵，由（1）知，A²=A，用A^-1左乘A²=A的两边，得A=E.又由题设A=E-αα^T，因而αα^T=O，故α=0，这与α是非零列向量矛盾.故A是不可逆矩阵.