矩阵相等：同型矩阵A和B的元素对应相等

（1）矩阵相等：如果两个矩阵A=（a_ij）m×n和B=（b_ij）m×n是同型矩阵，且a_ij=b_ij（i=1，2，…，m；j=1，2，…，n），则称这两个矩阵相等，记作A=B.

（2）矩阵的加、减法：设A=（a_ij）m×n，B=（b_ij）m×n是同型矩阵，则

设矩阵A=（a_ij）m×n，矩阵A的负矩阵，记作-A，即

则

矩阵加法满足下列运算规律（设A，B，C都是同型矩阵）：

交换律 A+B=B+A；

结合律 （A+B）+C=A+（B+C）.

（3）数与矩阵相乘：设λ是一个实数，则

称为数λ与A的乘积.

数乘矩阵满足下列运算规律（设A，B是同型矩阵，λ，μ为数）：

结合律 （λμ）A=λ（μA）；

分配律 （λ+μ）A=λA+μA，

λ（A+B）=λA+λB.

（4）矩阵的乘法：设矩阵A=（a_ij）m×s，B=（b_ij）s×n，定义A与B的乘法运算如下：

C=AB=（c_ij）m×n，其中

特别注意两个矩阵能够相乘时，第一个矩阵的列数必须等于第二个矩阵的行数.

矩阵乘法满足下列运算律（假设下列运算都有意义）：

结合律 （AB）C=A（BC），

λ（AB）=（λA）B=A（λB）（其中λ是数）；

分配律 A（B+C）=AB+AC，(www.xing528.com)

（B+C）A=BA+CA.

特别注意矩阵乘法不满足交换律，即AB≠BA，也不满足消去律，即AB=CB，则A不一定等于C.

（5）方阵的幂：设A是n阶方阵，定义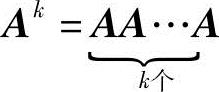，其中k为正整数.

方阵的幂满足下列运算律：

1）A^kA^l=A^k+l；

2）（A^k）l=A^kl.

（6）矩阵的转置：设矩阵A=（a_ij）m×n，则

称为A的转置矩阵.

矩阵的转置满足下列运算律（假设下列运算都有意义）：

1）（A^T）T=A；

2）（A+B）T=A^T+B^T；

3）（λA）T=λA^T；

4）（AB）T=B^TA^T.

（7）方阵的行列式：由方阵A的元素所构成的行列式，称为方阵A的行列式，记作A或detA.

方阵的行列式满足下列运算律（A，B都是n阶方阵，λ是数）：

1）|A^T|=|A|；

2）|λA|=|λⁿA|；

3）|AB|=|AB|.