线性代数学习辅导：阶行列式中含因子a11a23的项解析

1.利用对角线法则计算下列三阶行列式：

解 （1）

1×（-4）×（-1）-0×1×3-（-1）×2×8=-24+8-4+16=-4；

2.按自然数从小到大为标准次序，求下列各排列的逆序数：

（1）621354； （2）987654321；

（3）13…（2n-1）24…（2n）； （4）13…（2n-1）（2n）（2n-2）…2.

解 （1）t=2+1+1+2+1+0=7；

（2）t=8+7+6+5+4+3+2+1+0=36；

（3）

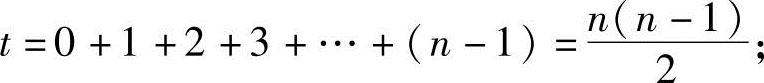
（4）t=（2n-2）+（2n-4）+…+4+2+0=n（n-1）.

3.写出四阶行列式中含有因子a₁₁a₂₃的项.

解 由四阶行列式D=∑（-1）ta_1p1a_2p2…a_4p4，其中p₁=1，p₂=3，所以p₃，p₄分别为2，4的排列，即为：-a₁₁a₂₃a₃₂a₄₄和a₁₁a₂₃a34a42.

4.计算下列各行列式：

（1）解法一 化行列式为上三角形行列式.

解法二 用行列式按行（列）展开法则来计算.

注 本题可利用行列式按行（列）展开法则，并结合行列式的性质来简化计算.

5.证明：

证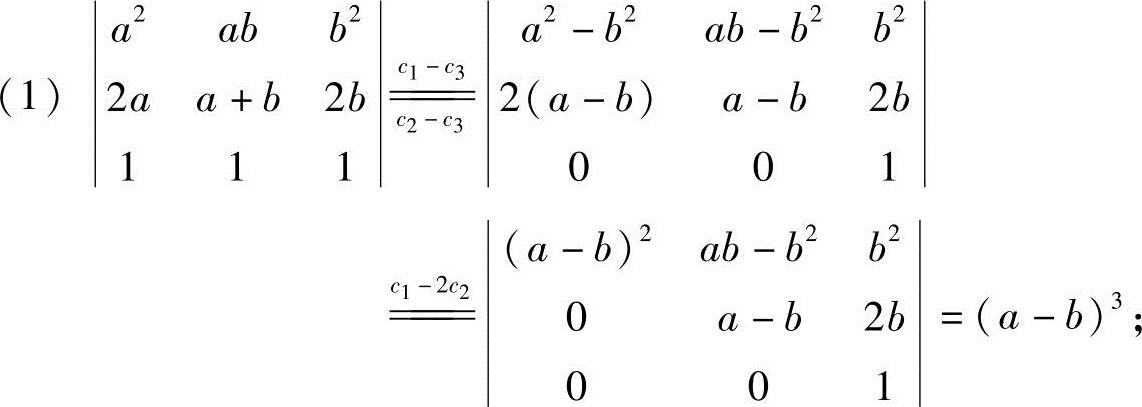

（2）左式按第一列拆开得

其中，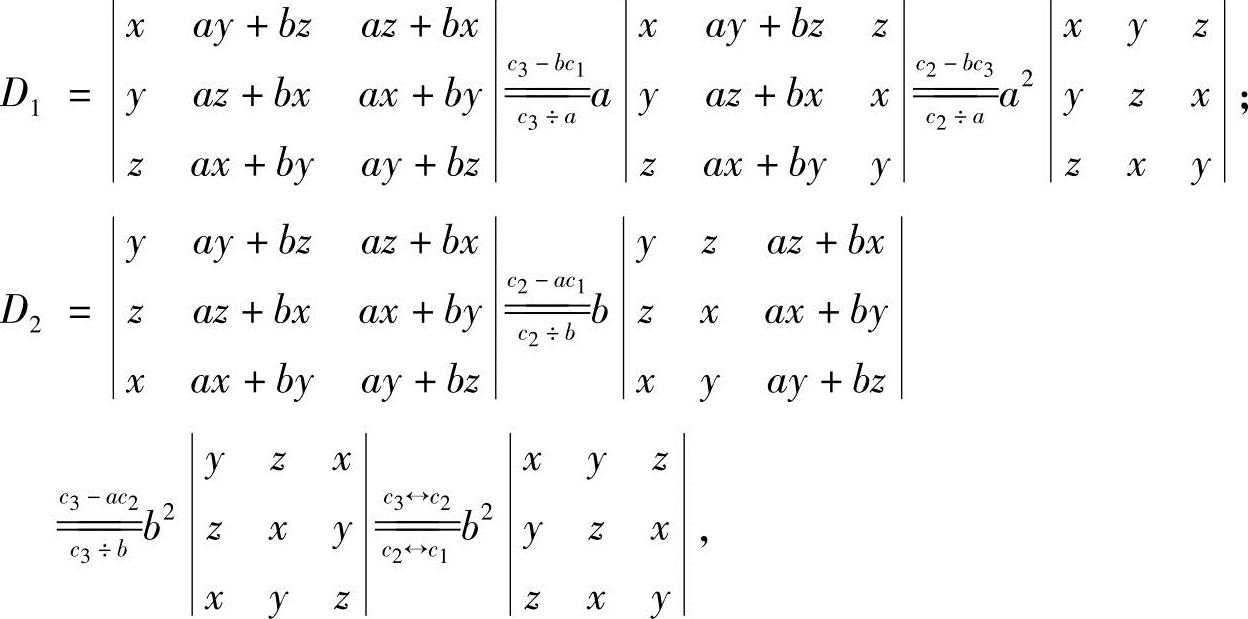

于是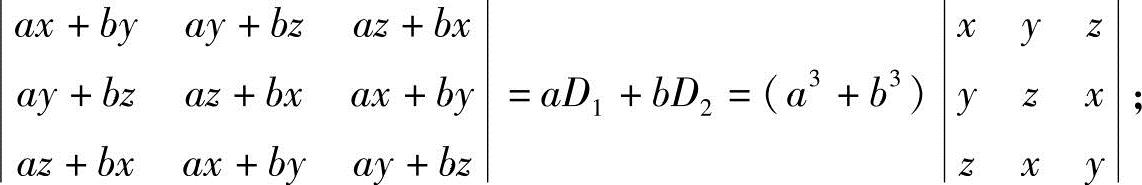

=0（因有两列对应成比例）；

（4）证法一

证法二 可将原行列式加上一行一列，变为范德蒙德行列式.

其中范德蒙德行列式第4行第5列元素的代数余子式

即原行列式等于范德蒙德行列式按第5列展开所得多项式中x³的系数的相反数.同时，它又等于式（1-3）右端展开式中x³的系数的相反数.即

（5）递推法.按第1列展开，以建立递推公式，

原式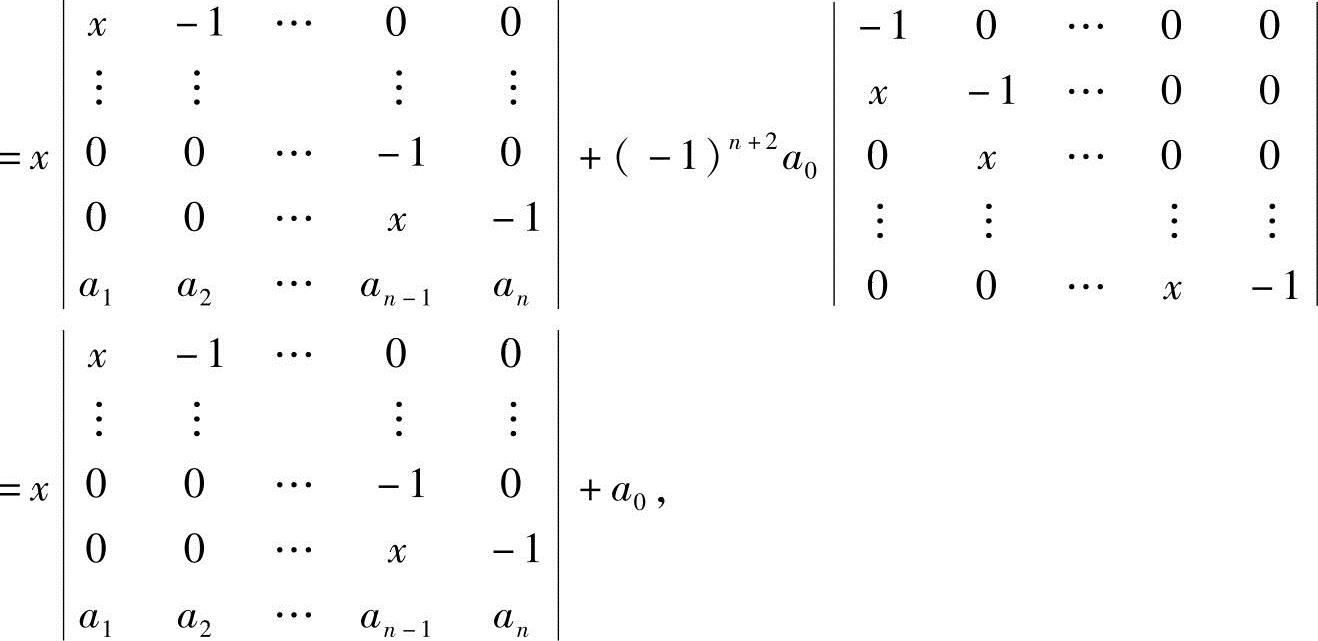

即

D_n+1=xD_n+a_0.

又，归纳基础为：D₁=a_n（注意不是x），于是

注 本题也可以将行列式按最后一行展开.

6.计算下列各行列式（D_k为k阶行列式）：

（1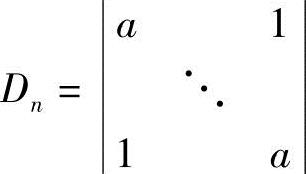），其中对角线上元素都是a，未写出的元素都是0；

（2）

（3）

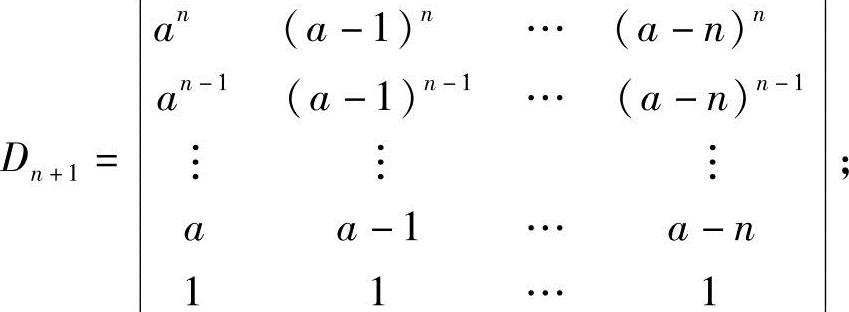
提示：利用范德蒙德行列式的结果.

（4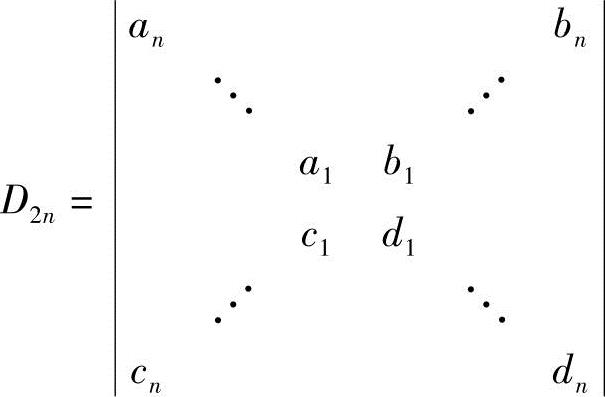），其中未写出的元素都为0；

（5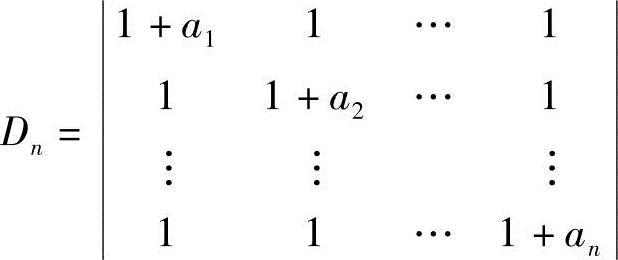），其中a₁a₂…a_n≠0.

解 （1）解法一 把D_n按第一行展开，得

解法二 把D_n化为上三角形行列式.

（2）利用各列的元素之和相同，提取公因式.

（3）把所给行列式上下翻转，即为范德蒙德行列式，若再将它左右翻转，由于上下翻转与左右翻转所用交换次数相等，故行列式经上下翻转再左右翻转其值不变，于是按范德蒙德行列式的结果，可得

（4）把D_2n中的第2n行依次与第2n-1行，…，第2行对调（作2n-2次相邻对换），再把第2n列依次与第2n-1列，…，第2列对调，得

由此得递推公式

D_2n=（a_nd_n-b_nc_n）D₂（n_-1），

另一方面，归纳基础为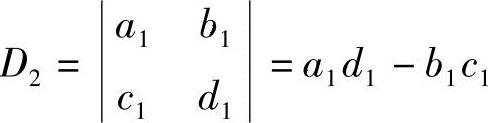，利用这些结果，递推得

（5）解法一 将原行列式化为上三角形行列式.

解法二 拆分法.先对最后一列进行拆分，

其中，(www.xing528.com)

得递推公式

D_n=a₁a₂…a_n-1+a_nD_n-1，

由递推公式，可得

D_n-1=a₁a2…a_n-2+a_n-1D_n-2，

代入得

D_n=a₁a₂…a_n-1+a₁a₂…a_n-2a_n+a_n-1a_nD_n-2，



D_n=a₁a₂…a_n-1+a₁a₂…a_n-2a_n+…+a₂…a_n-2a_nD₁，

又D₁=1+a₁，故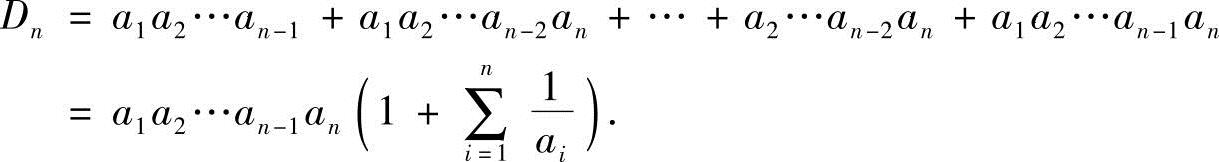

7.设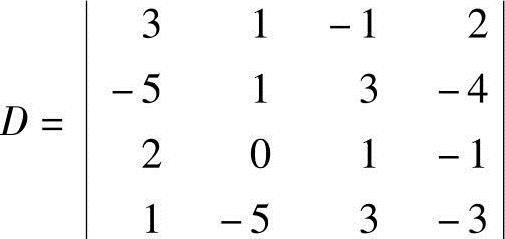，D的（i，j）元的代数余子式记作A_ij，求A₃₁+3A₃₂-2A₃₃+2A_34.

解A₃₁+3A₃₂-2A₃₃+2A₃₄等于用1，3，-2，2替换D的第3行对应元素所得行列式，即

8.用克拉默法则解下列方程组：

解 （1）

由克拉默法则，得

由克拉默法则，得

9.问λ取何值时，齐次线性方程组

有非零解？

解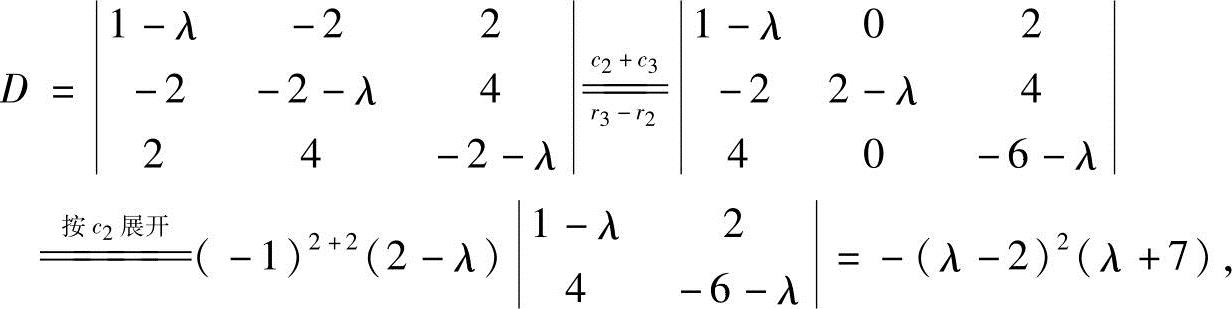

由D=0时对应的齐次线性方程组有非零解，得λ=2或λ=-7.

不难验证，当λ=2或λ=-7时，所给方程组有非零解.

10.已知△ABC的三个顶点分别是A（1，2，3）、B（3，4，5）和C（2，4，7），求△ABC的面积.

解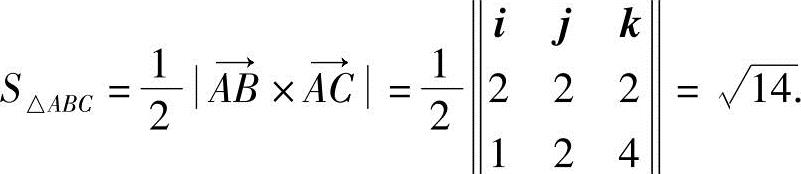

11.已知不在同一平面上的四点A（1，2，3）、B（3，6，5）、C（5，8，7）和D（4，6，2），求四面体ABCD的体积.

解 由立体几何知道，四面体的体积等于以向量AB、AC和AD为棱的平行六面体的体积的六分之一，因而四面体ABCD的体积

实验1

MATLAB是以矩阵为基本变量单元的.输入时，矩阵的元素用方括号括起来，行内元素用逗号分隔或空格分隔，各行之间用分号分隔或直接回车.语句的结尾可用回车符或逗号，此时会立即显示所得的结果，若不希望显示中间结果，则以分号结尾，此时运算仍然执行，只是不显示.

1.输入矩阵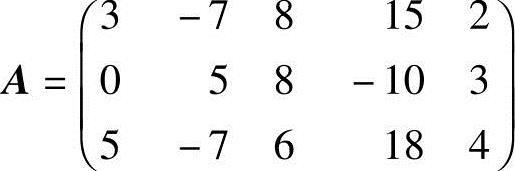，并提取矩阵A的第3列和第2行元素.

解 在命令窗口中输入语句

>>A=[3-78152；058-103；5-76184]；

>>A（：，3） %提取矩阵A的第3列的元素

运行结果为：

ans=

8

8

6

>>（2，：） %提取矩阵A的第2行的元素

运行结果为：

ans=

0 5 8 -10 3

注 %后面为注释语句，在程序中不运行.

2.计算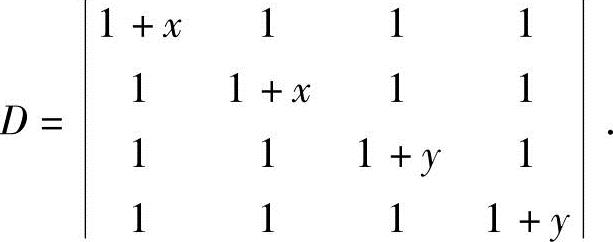

解 程序设计如下：

>>clear %该命令清除工作空间中变量与函数，以便保证程序顺利进行

>>symsxy%定义符号变量x，y

>>A=[1+x111；11+x11；111+y1；1111+y]；

>>D=det（A）%求方阵A的行列式

运行结果为

D=

x^2*y^2+2*x^2*y+2*x*y^2