线性代数学习辅导：典型例题解答及计算行列式

例1.1 设

则x⁴项的系数为（ ），x³项的系数为（ ），常数项为（ ）.

解 含有x⁴项的是a₁₁a₂₂a₃₃a₄₄，即8x⁴，故x⁴的系数为8.含有x³项的是-a₁₂a₂₁a₃₃a₄₄和-^a₁₄a₂₂a₃₃a₄₁，即^-12x³和^-2x³，故x³的系数为-14.常数项为f（0），即

故应依次填8，-14，-2.

例1.2 计算行列式

解

例1.3 设行列式

为f（x），则方程f（x）=0的根的个数为（ ）.（1999年，考研，数学二）

（A）1； （B）2； （C）3； （D）4.

解 将第一列乘以-1依次加到其余各列，再把第二列加到第四列上去，有

易见f（x）是二次多项式，故应选（B）.

例1.4 设有行列式

已知1703，3159，975，10959都能被13整除，不计算行列式D，试证明D能被13整除.

解 要证明行列式D能被13整除，也就是要证明行列式D含有因子13.通常的方法是证明行列式某一行或某一列各元素有公因子13，所以利用行列式的性质改变此行列式，使得行列式的某一列有公因子13.

由题设条件知，上式右端行列式的第4列各元素有公因子13，再由行列式性质可知，该公因子13可以提到行列式外边来，于是得

由此看出上式右端的行列式为一整数，故行列式D能被13整除.

例1.5 设abcd=1，行列式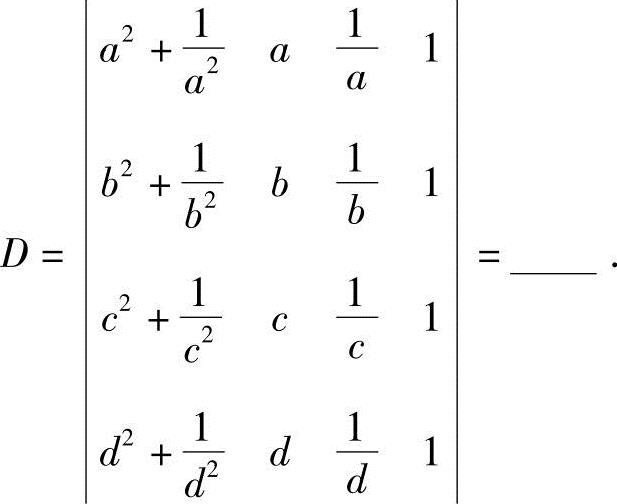

解 利用行列式的性质（5）可得

例1.6 计算三阶行列式(www.xing528.com)

解 将三阶行列式“加边”变成一个四阶行列式，即

例1.7 设行列式

则第四行各元素余子式之和的值为.（2001年，考研，数学四）

解法一 根据余子式的定义，即

解法二 利用代数余子式求解，即

例1.8 计算四阶行列式

解 本行列式为范德蒙德行列式，其中，x₁=1，x₂=2，x₃=3，x₄=4，所以可直接利用范德蒙德行列式的公式求解.

原式=（x_i-x_j）=（x₄-x₃）（x₄-x₂）（x₄-x₁）（x₃-x₂）（x₃-x₁）（x₂-x₁）

=（4-3）（4-2）（4-1）（3-2）（3-1）（2-1）=1×2×3×1×2×1=12.

例1.9 计算行列式

解 按最后一行展开，可得

例1.10 解线性方程组

解

于是得

例1.11 如果齐次线性方程组

有非零解，试求λ.

解 若所给齐次线性方程组有非零解，则其系数行列式D=0，而

由D=0，得λ=-2或λ=1.