如何确定每天报纸数量提高报童收入？案例分析

问题：报童每天清晨从邮局购进报纸零售，晚上卖不出去的退回。设报纸每份的购进价为 b ，零售价为 a ，退回价为 c 。根据实际情况，应有a ＞ b ＞c。请你给报童筹划一下，他应如何确定每天购进报纸的数量，以获得最大的收入。

分析：报童购进报纸数量应根据需求量来确定，但需求量是随机的，所以报童每天如果购进的报纸太少，不够卖的，会少赚钱；如果购进太多，卖不完就要赔钱，由于每天报纸的需求量是随机的，致使报童每天的收入也是随机的，因此衡量报童的收入，不能是报童每天的收入，而应该是他长期(几个月、一年)卖报的日平均收入。从概率论大数定律的观点看，这相当于报童每天收入的期望值，以下简称平均收入。

假设报童已经通过自己的经验或其他渠道掌握了需求量的随机规律，即在他的销售范围内每天报纸的需求量为 r 份的概率是f(r)( r=0,1,2,… )。

设报童每天购进 n份报纸，因为需求量 r是随机的，r 可以小于 n，等于 n，或大于 n；由于报童每卖出一份报纸赚a - b，退回一份报纸赔b - c，所以当这天的需求量r ≤n，则他售出 r份，退回n -r份，即赚了(a -b )r，赔了(b -c )(n -r )；而当r ＞n时，则 n份全部售出，即赚了(a -b) n。

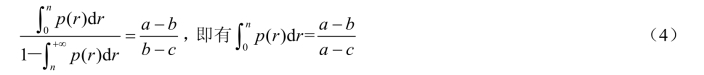
根据需求量的概率密度p(r)的图形(如图1)，很容易从(3)式确定购进量 n。

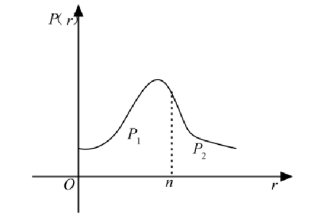
图1(www.xing528.com)

在图1 中，用 1p ， p2 分别表示曲线p(r)下的两块面积．则（3）式又可记作：

（5）式表明：购进的份数 n 应该使卖不完与卖完的概率之比，恰好等于卖出一份赚的钱a - b与退回一份赔的钱b - c之比。显然，当报童与邮局签订的合同使报童每份赚钱与赔钱之比越大时，报童购进的份数就应该越多，这与实际直观相吻合，所以图1 和（3）式有很强的直观意义。

例1 若每份报纸的购进价为0.15 元，售出价为0.2 元，退回价为0.12 元，需求量服从均值500 份、均方差50 份的正态分布，报童每天应购进多少份报纸才能使得平均收入最高，这个最高收入是多少?

即每天购进516 份报纸。按照（2）式，可得最高收入G=23.484元。

点评 案例9 涉及随机变量及其分布、数学期望及其意义、微积分优化，特别是巧妙地将离散问题连续化，将级数转化为积分，案例内容贴近生活，所得结论具有直观意义。此案例也是数学建模课程的极佳素材。此案例由给排水2014 级01 班张岑帆同学（201400860）提供，入选时经过校正和修改。