通过抽样方式理清离散分布的关系与区别

1.史料分析

历史上，人们确实是借助试验来不断认识和研究概率统计问题，试验确实是研究概率统计问题的出发点和重要途径。历史上有一些著名的试验，德·摩根（De Morgan）、蒲丰（Buffon）和皮尔逊（Pearson）曾进行过大量掷硬币试验，所得结果如表1 所示。

表1　历史上的掷硬币试验

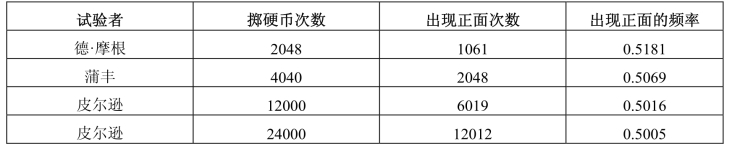
可见出现正面的频率总在0.5 附近摆动，随着试验次数增加，它逐渐稳定于0.5，这个0.5 就反映正面出现的可能性的大小。

每个事件都存在一个这样的常数与之对应，因而可将频率 f n( A) 在n 无限增大时逐渐趋向稳定的这个常数定义为事件A 发生的概率。这就是概率的统计定义。

定义 设事件A 在n 次重复试验中发生的次数为k，当n 很大时，频率 k /n在某一数值p 的附近摆动，而随着试验次数n 的增加，发生较大摆动的可能性越来越小，则称p 为事件A 发生的概率，记为 P ( A) = p。

这里要强调两点：一是，上述试验及概率的统计定义并没有提供确切计算概率的方法，因为我们永远不可能依据它确切地确定任何一个事件的概率。在实际中，我们不可能对每一个事件都做大量的试验，况且我们不知道n 取多大才行；如果n 取很大，不一定能保证每次试验的条件都完全相同。而且也没有理由认为，取试验次数为n+1 来计算频率，总会比取试验次数为n 来计算频率将会更准确、更逼近所求的概率。但是，上述试验的直观结果和客观规律是进行进一步理论研究的源泉，人们借助计算机来模拟大量重复试验，得到Monte Carlo 方法来计算π 的近似值和许多类似计算任务（参见案例3）。二是，上述概率的统计定义是不严谨的，其含义应当是指“随着n 的增大，对任意ε ＞ 0，概率P{ | f n( A) -P ( A)|≥ ε } → 0”，但这样一来，人们就陷入一个难以摆脱的怪圈之中：即用概率定义概率！

事实上，正是人们面对这种局面，从频率的稳定性和频率的性质受到启发，并不断地火热地思考着，开始探讨完善概率论自身的理论基础问题。1900 年的国际数学家大会上，Hilbert 提出的20 世纪应解决的23 个数学问题中也包括这个问题。自20 世纪30 年代苏联数学家Kolmogorov 建立了概率的公理化定义和概率的公理化体系后，概率论的严密的数学理论基础建立，后来的贝努利大数定理完整地刻画了“频率接近概率”的客观事实。

2.问题引入——事件的表示与不同抽样方式下古典概率的计算

事件的合理、简洁表示，特别是如何表示复合事件，是学习概率的一项基本功，也是概率的基础内容。

常见的抽样方式有两种：

①第一次随机取一只球，观察其颜色后再将其放回，搅匀后再随机取一球，如此继续，这种抽样方式叫作放回抽样；

②第一次随机取一只球，观察其颜色后不再放回，第二次从剩余的球中再随机取一球，如此继续，这种抽样方式叫作不放回抽样。

任何概率问题好像可以与一个研究袋中抽球的适当问题相比拟。今天，我们也像古人一样，借助以上两种抽样方式来研究古典概率问题。

问题：箱中装有a 只白球，b 只黑球，它们除颜色不同外，质地、大小、形状等其他特性没有任何区别。从袋中随机抽球，每次抽一个。以下是4 类事件（因k 可变，k 取定即为一个事件）：

（1）第k 次抽到白球；

（2）第k 次抽球时首次取到白球；

（3）第k 次抽球时恰取到白球r 次；

（4）抽取n 次，其中有k 次白球。

第一问：试分别表示这4 类事件；

第二问：在放回抽样下分别计算这4 类事件发生的概率；

第三问：在不放回抽样下分别计算这4 类事件发生的概率；

第四问：试分别引入4 个随机变量表示这4 类事件；

第五问：在放回抽样下分别求这4 个随机变量的分布律，并讨论这4 个随机变量的关系；

第六问：在不放回抽样下分别求这4 个随机变量的分布律，并讨论这4 个随机变量的关系；

第七问：分析放回抽样与不放回抽样的本质区别，以及两类离散型随机变量的区别；

第八问：你还能得到哪些启示或结论？

3.问题的分析与解答

3.1 第一问的分析与解答——事件的合理表示

3.2 第二问的分析与解答——放回抽样下，事件 Ai间相互独立

3.3 第三问的分析与解答——不放回抽样下，事件 Ai间不相互独立

3.4 第四问的分析与解答——随机变量的引入，便于应用数学方法研究随机现象

概率论是通过随机试验来研究随机现象的统计规律性，实质上是研究某个随机试验所对应的随机变量取值的分布规律。所谓随机变量，通俗地理解就是将某个随机试验的每个结果（或样本点）赋予一个实数，即将某个随机试验的每个随机结果数量化。用数学语言来讲，随机变量就是定义在某随机试验的样本空间上的、以样本点为自变量的函数，由于样本点的出现是随机的，所以对应的函数值（或随机变量的取值）也是随机的，人们关心的是某个随机试验所对应的随机变量取任何值的概率，进而可得到该随机变量在任意给定范围内取值的概率。

关于随机变量的研究，是概率论的中心内容。引入随机变量，更便于应用数学方法研究随机现象，概率论就能从计算一些孤立事件的概率发展为一个更高的理论体系。可以说，随机变量是比随机事件更广的概念，随机事件是从静态的观点来研究随机现象，而随机变量则是一种动态的观点。

令

(www.xing528.com)

X 表示首次抽到白球时已抽到的球的总数， Y 表示第r 次抽到白球时已抽到的球的总数,Z 表示抽取n 次时其中白球的个数，可知，X k， X， Y， Z都是随机变量，它们的取值都是动态可变的、随机的。用随机变量分别表示这4 个事件，如下：

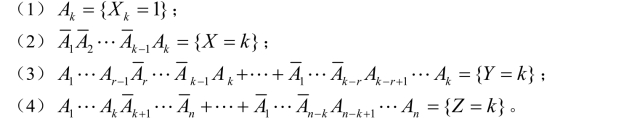
3.5 第五问的分析与解答——放回抽样下，随机变量Xk间相互独立

列出某随机变量取各个值的概率，就得到该随机变量的分布律。

在放回抽样下，事件 Ak 间相互独立，就相当于随机变量X k间相互独立。由上文可知，在放回抽样下，这4 个随机变量的分布律分别如下：

从而，在放回抽样下，得到了无穷个独立同(0,1)分布、几何分布、负二项分布、二项分布及其各相应的随机变量，这些都是放回抽样下对应的重复独立试验概率模型，这一类离散分布内部之间的关系是通过事件或随机变量之和或之积来实现的，它们的内部关系具体如下：

3.6 第六问的分析与解答——不放回抽样下，随机变量Xk间不相互独立

在不放回抽样下，事件 Ak 间不相互独立，就相当于随机变量Xk间不相互独立。由上文可知，在不放回抽样下，这4 个随机变量的分布律分别如下：

从而，在不放回抽样下，得到了有限个非独立同(0,1)分布、类几何分布、类负二项分布、超几何分布及其各相应的随机变量，这些也都是“不放回抽样”下对应的多次不独立试验概率模型，这一类离散分布内部之间的关系是通过事件或随机变量之和或之积来实现的，它们的内部关系具体如下：

①“类几何分布”是k 个不独立同(0,1)分布的联合分布下的其中一个取值；

因为，其分布可根据条件概率表示为

②“类负二项分布”是k 个非独立同(0,1)分布的联合分布下的其中一个取值；

因为，其分布可表示

3.7 第七问的分析与解答——放回抽样与不放回抽样决定了两类离散分布及其随机变量，其本质区别就是独立性与非独立性

由上文可知，在放回抽样下，得到了无穷个独立同(0,1)分布、几何分布、负二项分布、二项分布及其各相应的随机变量；在不放回抽样下，对应地得到了有限个非独立同(0,1)分布、“类几何分布”“类负二项分布”、超几何分布及其各相应的随机变量。

总之，在放回抽样与不放回抽样不同的抽样背景下，产生了两类离散分布，这两类离散分布及其具体对应分布之间的本质区别就是事件或随机变量之间的独立性与非独立性，这恰好是由两种不同的抽样方式所决定的。所以，可将“放回抽样”与“不放回抽样”看成两个不同的“参数”，原问题在“放回抽样”这个参数下，得到了无穷个独立同(0,1)分布、几何分布、负二项分布、二项分布及其各相应的随机变量，这些都是“放回抽样”下对应的重复独立试验概率模型，概率计算中应用了独立性和有限可加性（通过组合数实现加法原理）；在“不放回抽样”这个参数下，对应地得到了有限个不是独立同(0,1)分布、“类几何分布”“类负二项分布”、超几何分布及其各相应的随机变量，这些也都是“不放回抽样”下对应的多次不独立试验概率模型，概率计算只应用了古典概率公式和条件概率公式（通过排列数实现乘法原理）。

3.8 第八问的分析与解答——科学研究就像解剖一只麻雀

一个好的问题能激发人们的无限想象与探求欲望，一个好的问题可以贯穿学科的理论体系。可以看出，在司空见惯的抽球问题中，涉及试验、随机事件、概率的性质、古典概率、条件概率、独立性、随机变量、事件或随机变量的函数关系（和，积）、复合事件或随机变量的分解方法等等概率论中的诸多中心知识。

对上文已阐述的内容，归纳为（1）（2）（3）三点，此外得到以下（4）（5）（6）（7）四点启示。

（1）放回抽样与不放回抽样决定了两类离散分布及其随机变量，其本质区别就是独立性与非独立性；

（2）各类离散分布内部之间的关系可通过事件或随机变量之和或之积来表示；

（3）随机事件或随机变量的引入，依据人们的实践需要和理论需要；

（4）两个重要原理：条件概率原理和抽签公平原理。

正如前文所说，任何概率都是条件概率。原问题在“放回抽样”与“不放回抽样”这两个不同的“参数”或条件下，分别得到一系列相应的分布。任何概率都是条件概率，就像任何事物都是在一定条件下存在并具有相应性质一样，都是客观事实。从而任何分布都是条件分布，任何事件都是在给定条件下发生。笔者认为这是概率统计中的一条重要原理，但是现行教材强调不够，基本上都处理的是“放回抽样”的情形，对大样本的“不放回抽样”常常近似地当作“放回抽样”。但是，很多实际问题中都是小样本下的“不放回抽样”，比如航天飞行器等一些代价昂贵且具有破坏性的一类试验都是不放回抽样。因此，笔者认为，“类几何分布”“类负二项分布”这几个不放回抽样下的分布的理论价值和实际应用无疑值得我们去研究，但现行教材都没有涉及。

也如上文所说，在不放回抽样下，虽然 Ai 之间不是相互独立的，但当球的总数a + b很大（或趋于无穷大）情形下的不放回抽样可近似当作（或趋于）放回抽样来处理，这也是放回抽样下几何分布、负二项分布、二项分布、泊松分布广泛应用的一个原因，也是不放回抽样下的几个分布（除超几何分布外）没有被研究者重视的一个原因，大总数下的超几何分布也常常近似当作放回抽样下的二项分布来处理，因为不放回抽样下的精确分布比较复杂，不便于实际应用。所以，当球的总数a +b 很大（或趋于无穷大）情形下的不放回抽样可近似当作（或趋于）放回抽样来处理，正如当总体中个体数目很大时，常常当作无限总体来近似处理一样，这就是人们将未知复杂事物近似简化为结构相似或性质相似的已知简单事物来处理的一般方法。

（6）运用问题教学法，培养探索精神；运用讨论式教学法，激发主动学习热情

问题教学法就是指通过提出问题、分析问题、解决问题的方式而进行的教学方法。这种方法有助于学生养成积极思考、新颖好奇、敢于批判、勇于超越等良好的心理品质，是培养探索精神的一种有效方法。对概率统计的许多新概念、新理论、新方法的教学，可以采用这种方式向学生展示它的实际背景、演变过程，使学生从整体上体会知识的探索过程，把握知识体系的发端、推进和提升，融会贯通地领悟其中蕴含的数学思想与精神。

讨论式教学法是师生共同完成教学任务的一种教学方法，它打破了教师满堂灌教学模式。通过这种方法，让学生开动脑筋，积极思考，大胆发表意见，自由辩论，提出质疑，共同探讨，激发主动学习的热情和科研兴趣。同时，也增进了师生之间的思想交流，促使教师不断学习，更新知识，提高讲课技能。

（7）提高数学课堂教学效率必须进行教学研究

在现行教材及教学中，往往是按(0,1)分布、二项分布、泊松分布这样的逻辑顺序讲授离散分布的，对其他离散分布（如几何分布、负二项分布、超几何分布等）及其关系涉及很少，这是一个缺憾！这样的处理方式没有充分揭示二项分布在常见离散分布中的核心地位，不能揭示两类离散分布的本质区别，更不能揭示人类认识这几个离散分布的历史过程。正是由于放回抽样下的负二项分布、二项分布、泊松分布有一脉相承的内在关系，才使得它们具有“可加性”的共同特性。因此，笔者建议，在离散分布的教学中通过类似的问题，既突出了两类离散分布之间的内在关系及二项分布的核心地位，又突出了放回抽样与不放回抽样在概率统计中的重要作用，还得到了“类几何分布”“类负二项分布”“类泊松分布”，这几个分布只是抽象的思维模型吗？在实际问题中是否存在对应的应用模型？它们的理论价值和应用价值怎样？尽管不放回抽样下的这几个分布比较复杂，不便于实际应用，但是我们在能得到它们的精确分布的情况下，何尝不去应用呢？这样不是可以更精确地认识随机现象的统计规律性吗？事实上，这几个分布在非独立小样本统计推断中有着重要的应用。

总之，笔者认为，提高数学课堂教学效率就应该在刻画数学知识与数学思想方法最本质的实质内容方面下功夫，一线教师应深入挖掘、钻研所教数学内容，理清数学知识与数学思想方法之间联系、发展的内在数学知识结构体系，甚至去“改造”前人留给我们的数学知识体系，使得更科学便捷地为学生所接受，使学生的数学认知结构得到高效率的改善与提高，事实上，这正是“教育数学”所关注的中心问题。所以，提高数学课堂教学效率，为一线数学教师的教学研究与教学创新预留了足够的空间，它伴随着每位研究型教师的成长过程，是提高课堂教学效率不可或缺的重要环节。这里，只是一次初步的尝试，希望能抛砖引玉，以求真知灼见，为学生而数学，为数学而教育。