释压造坝人的心路历程

扬压力是水工建筑物的一项重要荷载。

本文主要谈谈岩基上重力坝的扬压力。

现在在重力坝的设计工作中，按规范确定设计扬压力的方法看来是很简单的。然而，这一“简单的”方法，却是人们在经历了对扬压力复杂而曲折的探索历程之后才获得的。

人们对扬压力的认识，从无所知到有所知，从对它有模糊的概念到进行较准确的计算，已经经历了一个多世纪的漫长时期。这是扬压力与作用在坝体上其他荷载如坝体自重等迥然不同之处。甚至到了今天，我们对扬压力的认识也并非进入到了自由王国的境界，还存在有待进一步研究的问题。

从历史的角度看，人们对扬压力这一重要荷载的认识过程，大体上可分为以下三个阶段。

（1）无所知阶段——1882年以前

1882年以前，扬压力这一特殊荷载尚不为人所知。尽管19世纪中叶以后，水坝的发展已进入近代坝阶段，开始用理论指导设计。继法国富伦斯（Furens）坝之后，还建成了一批近代重力坝。然而这些坝的设计竟然均没有考虑扬压力。但又值得注意的是，这些坝的绝大多数又并未因没有考虑扬压力而失事。这一事实后来竟成了某些人［如韦格曼（Wegmann，E.）］怀疑扬压力是否真的存在的理由。实际上这些近代坝的绝大多数之所以能安全运行，明显的是由于其他因素在当时使坝体产生了安全裕度，从而弥补了没有考虑扬压力所带来的危险，如当时设计坝体时所采用的容许应力值就很低。

（2）裂缝理论阶段——1882年至20世纪30年代

英国工程师迪肯（Deacon，G.F.）在1882年最先提出了扬压力的概念。但是，迪肯的这一重要发现在当时并未引起广泛重视，只是在英国国内的坝工建设中有意在坝内设置了碎石排水管系统以降低坝身扬压力，如1882～1891年建成的凡威（Vyrnwy）坝就采用了这种措施。该坝用于利物浦城市供水，坝高41.5m，长411.5m，是世界第一座在设计中考虑了坝身扬压力的大坝，如图1所示。

图1　凡威坝（引自R.B.Jansen）

扬压力真正被人们注意，倒要“归功”于以下三座水坝的失事。

1）1895年法国布泽衣（Bouzey）坝的失事。

2）1900年美国奥斯汀（Austin）坝的失事。

3）1911年美国宾夕法尼亚州一座水坝的失事。

这三座水坝的失事促使人们不得不重新评价当时的坝工设计理论与方法，其中包括是否应考虑扬压力的问题。布泽衣坝失事后，利维（Levy，M.）就立即分析了该坝失事的原因，并在当年8月5日向法国科学院呈交了一份报告，明确指出在该坝的上游面裂缝中存在有扬压力，并提出了一条有关砌石重力坝的设计准则，这就是著名的“利维准则”。这一准则的内容是：为了防止库水渗入坝内产生扬压力，砌石重力坝上游面某点的压应力必须大于同一高程上的水库水压力。换句话说，砌石坝本来是不透水的，因而也不存在扬压力，只有一旦出现裂缝并渗进了水，坝体才产生扬压力；而如果上游面的压应力大于同一高程上的水压力，就不致出现裂缝，因而也就不会有扬压力作用于坝体了。现在看来，利维所要求的上述条件过于保守，以致过去许多年间用这一准则所设计的重力坝都造成了巨大的浪费。

与此同时，鉴于布泽衣坝的失事，美国土木工程师协会的范伯恩（Van Buren，J.D.）建议：在设计砌石重力坝时，整个坝基都应考虑作用有其值等于水库静水压力的扬压力；对坝内任一水平截面，也按这一原理处理。范伯恩曾经应用他的这一建议设计过一座砌石坝，坝高为76m，而坝底宽竟达107m。

后来的工程师们都采用了比范伯恩建议小的扬压力值。在美国马萨诸塞州，于1900～1906年建造的为波士顿给水工程服务的瓦丘塞特（Wachusett）坝的设计中，美国土木工程师协会前主席斯特恩斯（Frederic P.Stearns）也曾假定在整个坝基上都作用有扬压力，但在上游坝踵处等于库水压力的2／3，然后均匀减小到下游坝趾处为零。瓦丘塞特坝是世界上第一座在设计中考虑了坝基扬压力的砌石重力坝，坝高62.5m，坝顶长288m，用于供水与发电，图2是其下游立视图。坝后是一个水池，景观秀丽。

在这一阶段，人们对扬压力的认识虽然取得了一定的进展，但直到20世纪30年代还处于一种半信半疑的状况，这反映在当时的权威著作韦格曼的《坝的设计与施工》（The Design and Construction of Dams）一书中。韦格曼在该书中指出：尽管当时人们认识到有扬压力存在，可是自1860年之后在世界各地修建的40多座高于21m的砌石坝都是成功的，它们在设计中并未考虑扬压力。韦格曼还认为，上述三座失事的坝（这三座坝均低于21m），如果要将其失事的原因归咎于扬压力的话，那也主要是因为这三座坝的地基太差。也就是说，如果地基坚硬完整的话，是不会因为扬压力而失事的。

图2　瓦丘塞特坝下游立视图（引自en.structurae.de）

在这一阶段，人们对扬压力的认识有一个共同点：认为只有当坝体或地基事先存在有裂缝，才会在渗水之后在裂缝中产生扬压力——我们不妨称之为“裂缝理论”。这种理论持续到20世纪30年代才为新的理论所替代。持这种理论的人除上述的利维和韦格曼之外，还有雷克斐尔德（Lieckefeldt）和林克（Link）。此外，还有旭克利许（Schoklitsch，A.），他在20世纪20年代末，对扬压力问题提出了如下灼见，可作为裂缝理论的一个总结。

1）对于所设计的重力坝，如果能绝对保证在坝面不出现拉应力，则不会有裂缝，因而水就无法渗进去。因此，设计完善的坝，就可以不考虑扬压力。不过为了特别慎重起见，还是在坝体内设置排水管为好，以排出万一渗进去的渗水。(www.xing528.com)

2）如无特殊的防渗措施，库水很容易渗进到坝与地基的交界面中。因此，要考虑坝基的扬压力。坝基扬压力的分布图与交界面中的渗水在坝趾处是否能自由出流有关。如果能自由出流，则呈三角形分布，上游起点处的扬压力即等于库水压力，直线减少到坝趾处为零，如图3中ABC所示。如不能自由出流，则呈矩形分布，即整个坝基断面均作用有其值等于库水压力的扬压力，如图3中ABDC所示。

3）扬压力中超过由坝身自重和水压力所引起的坝底反力（坝底反力如图3中AEC所示）的部分，谓之“有效扬压力”。有效扬压力与扬压力的分布图形有关：对于三角形分布的扬压力，有效扬压力为ABF；对于矩形分布的扬压力，有效扬压力为ABG。两者相差部分BFG较小。因此，扬压力的分布究竟如何，关系不很大，并不像过去所想像的那么严重。

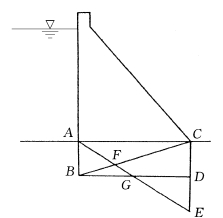
图3　旭克利许建议的扬压力分布图

4）为降低扬压力，可采取排水、灌浆等措施。

5）扬压力的存在，可使坝体所受合力向下游偏移，因而将改变坝底应力分布。

旭克利许在上述第2）点中所说的扬压力呈矩形分布的论点，在今天看来似乎已无什么实际意义，但给了我们一个重要的启示：坝与地基交界面的下游端以及坝趾处地基都要保证渗水自由出流，否则扬压力确有可能增大乃至大到沿坝底呈矩形分布的程度。

（3）孔隙理论阶段——20世纪30年代以后

自20世记30年代开始，世界各国都对扬压力进行了多方面的研究。与前一阶段比，这一阶段主要在如下两方面有所进步：一是研究的手段多了，现代化了；二是出现了新的理论——“孔隙理论”，取代了过去的“裂缝理论”。

在这一阶段，除了继续进行理论研究外，所采用的其他研究手段主要是对已建坝进行原型观测，以及有关的试验室试验。

各国在过去作了大量的原型观测工作，对坝基扬压力分布规律的观测结果大体上是相同的，即对于采取了帷幕灌浆与坝基排水的水坝，其坝基扬压力在帷幕与排水处要降低很多，其总的趋势如图4中的AEFN或ADN线所示。

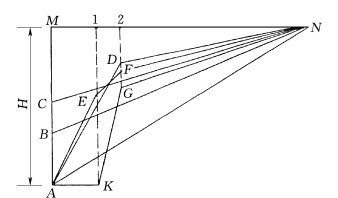
图4　扬压力分布图

1—帷幕；2—地基排水；H—坝体上、下游水头差

为了研究混凝土的渗透性，人们还做了大量的试验室试验。为了研究坝内的扬压力，卡尔逊（W.R.Carlson）和戴维斯（R.E.Davis）等人曾经进行了长达7年之久的渗透压力的观测工作，发现完整的坝体混凝土内也存在有渗透压力，即坝体混凝土并不是不透水的，只是离上游面不远处的渗透压力很小，而且也不一定随时间增加。

此外，现代研究手段的重要方面之一，就是利用电子显微镜对混凝土进行微观研究。实际上，混凝土是由颗粒胶结而成的多孔固体，粗骨料间有细骨料充填，细骨料间又有水泥胶结体。在7500倍电子显微镜下，可以见到水泥胶结体像连杆一样胶结着这些骨料，其中有大量的孔隙存在。在电子显微镜下的混凝土体的微观结构如图5所示。

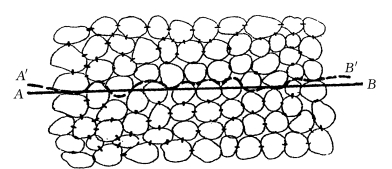
图5　混凝土内部结构图

混凝土是带有大量孔隙的物质，因而压力水可以渗透进去的这一事实，就使得认为混凝土是不透水的“裂缝理论”失去了理论基础。于是一种新的理论——“孔隙理论”应运而生。这一理论的出现，给扬压力的研究开辟了新局面。从此，人们便知道了混凝土是一种透水材料，压力水不一定要在混凝土存在有裂缝的条件下才能渗透到坝体内产生扬压力，就是在混凝土“完美无瑕”的条件下，压力水也能渗进到混凝土的孔隙中去产生扬压力。而且静水压力也不是像“裂缝理论”认为的只作用在坝体表面，而是作用在渗透水所至的坝体内部，如同重力一样同属于体积力范畴。此外，20世纪20年代由太沙基（Terzaghi，K.）在土力学中所创立的“有效应力”原理同样可应用到混凝土体，即混凝土骨料间的“接触力”为“有效应力”，孔隙中的水压力为“孔隙水压力”或“中性应力”。作了这样的处理之后，对坝体应力计算的解释就方便多了。新理论的创立应归功于费伦格尔（Fillunger）、太沙基、勒里亚夫斯基（Leliavesky）和克里盖尔（Creager，R.W.）等人。

伴随“孔隙理论”而提出的另一个问题，就是扬压力的“作用面积系数”，即扬压力的有效作用面积问题。对这一问题的研究，自20世纪30年代以来人们也作了大量的工作。

如图5所示，若从几何学的角度看，水平截面A—B所受的扬压力只有A—B所穿过的孔隙部分才有，而被固体颗粒所占有的那部分则没有扬压力，因而扬压力的作用面积系数就是一个远小于1的、与混凝土的“孔隙率”数值相等的值。但事实又并非如此，扬压力实际上几乎作用在100%的截面面积上。这一结论要归功于以下一些人的工作：太沙基、勒里亚夫斯基、哈扎（L.F.Harza）、麦克亨利（D.McHenry）、克里盖尔、格里申（Грищина M.M.）和弗雅逊斯基等人，他们通过试验研究证明该值接近于1.0。如勒里亚夫斯基的试验值为0.91；如果混凝土处于饱和状态，可修正为0.85。麦克亨利的试验也证明该值接近于1.0。一般说在0.93～0.95范围。之所以接近于1.0，是因为我们前面所考虑的直线A—B是一个理想的截面，实际上我们应该考虑的是一个在A—B线附近的、几乎完全穿过孔隙的不规则的截面，如图5中粗虚曲线A′－B′所示。所以，在20世纪60年代以后，作用面积系数等于1.0的结论已被各国的坝工规范所采用，包括我国的《混凝土重力坝设计规范》（SDJ21—78）（试行）。