简明运动生物力学：体育运动中的流体力学

凡是没有固定形状且易于流动的物体就称为流体。人体或器械的运动都是在流体（空气或水）环境中运动的，很多情况下流体（空气或水）对人体或器械运动的影响是不能忽略的。例如，各种球类运动、投掷运动、水中及水上项目的运动等，都会受到流体的作用从而影响其运动的效果。本节从运动生物力学的角度分析人体或器械在流体中的运动，研究如何根据流体的特性、采用合理的动作技术，减小在特定方向上流体的阻力、增大动力。

（一）静止流体内的压强

流体内部任何方向都有压强，在同一深度各个方向的压强都相等。流体内部某一深度的压强等于流体的密度（ρ）、重力加速度（g）、深度（h）三者的乘积，即P=ρgh。

（二）理想流体

流体在流动时各层间有相对滑动，相邻层间存在着摩擦力，称其为内摩擦力或黏滞力。实际上流体是可压缩的。液体压缩较难，气体压缩却很容易，很小的压强差就能导致气体迅速流动。在很多情况下，黏滞性和压缩性对流体的运动影响很小，是次要的因素，而流动性对其影响是主要因素。为了突出流体的这个主要特征，使问题简化，把定常的、无旋的、不可压缩和没有黏滞性的流体称为理想流体。

（三）流体具有流动性和黏滞性

人体的流体运动环境包括空气和水。流体的宏观力学性质是具有易流动性，这是流体区别于固体的属性。在真空状态下，运动的物体受到的阻力及升力为零。物体在流体中运动时，即使做匀速直线运动，物体也会受到流体的阻力。在速度较低的情况下，物体表面会附着一层流体随物体一起运动，从而使物体表面附着的流体层与邻近的流体层之间发生相对运动，由此产生阻碍物体运动的黏滞力，也称为黏滞阻力或摩擦阻力。

（四）流体质点和连续介质模型

流体质点（流体微团）是在研究流体机械运动中所取的最小的流体单元，它的体积无穷小却又包含无数多的流体分子，即微观上充分大、宏观上充分小的分子团。流体质点尺度比分子或分子运动尺度足够大，它可以包含“无数”个分子，而比所研究的力学问题的特征尺度又足够小。

将流体看成连续介质是流体力学研究的基本假设之一。它认为流体是由无数质点（流体微团）组成、质点间没有空隙、连续地充满其所占据的空间的连续体，且质点宏观物理量，如质量m、速度v、压强P、温度T等，各物理量之间可以用连续函数来表示，从而利用数学的方法研究流体的受力情况及运动规律。

（五）流动的分类

①按流体通过空间固定点时，其运动参数是否随时间变化来分类：

a.定常流动：是指在流场中流体中任何一点的运动参数（压力、速度、密度等）不随时间变化的流动，称为“稳态流动”或者“恒定流动”。

b.非定常流动：是指在流场中流体中任何一点的运动参数（压力、速度或密度等任意一个）随时间变化的流动。

②按与空间坐标变量的关系来分类：一维流动、二维流动和三维流动。

（六）流线和迹线

1.流线

流线是在流场中每一点上都与速度矢量相切的曲线（图4-7）。流线是同一时刻不同流体质点所组成的曲线，它是该时刻不同流体质点的速度方向。

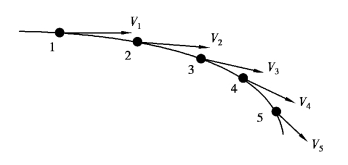
图4-7　流线

2.流线的性质

①在运动流体的整个空间，可绘出一系列的流线，称为流线簇。流线簇的疏密程度反映了该时刻流场中速度的不同。

②当为非定常流时，流线的形状随时间改变；当为定常流动时，流线的形状和位置不随时间而变化。

③一般情况下，流线不能相交，不能折转，只能是一条光滑曲线。

3.迹线

迹线是流体质点在空间运动时所描绘出来的曲线，即流体质点运动的轨迹。

4.迹线的特点

①迹线的切线给出的是同一流体质点在不同时刻的速度方向。

②迹线是单个质点在连续时间过程内的流动轨迹线。

③迹线只与流体质点有关，对不同的质点，迹线的形状可能不同。但对某一确定的质点而言，其迹线的形状不随时间变化。

（七）流管和流束

在运动流体空间内垂直于流动方向作一微小的闭合曲线，通过该闭合曲线上各点的流线围成的细管称为流管（图4-8）。由于通常情况下流线不会相交，因此，流管内、外的流体都不会穿越管壁。

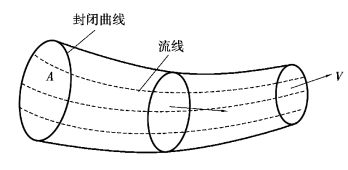
图4-8　流管和流束

在各个时刻，液体质点只能在流管内部或沿流管表面流动，而不能穿越流管。流线组成了流束，流束是流管内的流线簇。流管仿佛就是一根虚拟的水管，其周界可以视为虚拟的固壁。在日常生活中，自来水管的内表面没有流体的穿透，这一点与流管是相同的。但在自来水管的内表面上，流体被黏附导致速度为零，而流管壁并没有这种约束，两者之间还是有一定的区别。

（八）层流和湍流

层流和湍流是流体的一种流动状态。当流速很小时，它做层状的流动，流体分层流动，互不混合，称为层流，也称为稳流或片流[图4-9（a）]；逐渐增加流速，流体的流线开始出现波浪状的摆动，摆动的频率及振幅随流速的增加而增加，此种流况称为过渡流；当流速增加到很大时，流线不再清楚可辨，流场中有许多小漩涡，层流被破坏，相邻流层间不但有滑动，还有混合。这时的流体做不规则运动，有垂直于流管轴线方向的分速度产生，这种运动称为湍流，又称为乱流、扰流或紊流[图4-9（b）]。

图4-9　层流和湍流

（九）过流断面和流量

1.过流断面

某一研究时刻的流管或流束一个横断面，称过流断面。过流断面是与流管内所有流线正交的横断面，不一定是平面，其形状与流线的分布情况有关，只有当流线相互平行时，过流断面才为平面，否则为曲面。过流断面用S表示。

2.流量

流量是指单位时间内通过流管或流束中过流断面的流体量，用Q表示，Q=vS，其中v是流体的平均速度。流量的度量单位一般用体积，也可以用质量或重量。

（十）流体的连续性原理——连续性方程

这是描述流体流速与截面关系的定理。当流体连续不断而稳定地流过一个粗细不等的流管时，流管中任何一部分的流体都不能中断或挤压起来，在同一时间内，流进任意过流断面的流体质量和从另一过流断面流出的流体质量应该相等。即

ρ1v1S1=ρ2v2S2=常数

这就是流体运动的连续性方程式。如果是不可压缩流体，则ρ保持不变。连续性方程式即为

v1S1=v2S2=常数

可以得到结论：流束的平均流速与过流断面的面积成反比。即在流量一定的情况下，流束断面大则流速小，流束断面小则流速大。

（十一）流体的能量守恒原理——伯努利方程

利用功能原理（外力所做的总功等于机械能的增量）可以推导出理想液体做定常流动时的压强P、速度v和高度h之间的关系。

假设流体在重力场中做定常流动，全取一段细流管作为研究（图4-10）。由于流管取得非常小，可以认为在同一个过流断面截面上的每一点的流体的流速和压强都是相同的。设在左端，其截面积为S1、速度为v1、压强为p1、距离参考面的高度为h1；在右端，截面积为S2、速度为v2、压强为p2、距离参考面的高度为h2。S1-S2这段流体在极短的时间Δt（Δt=t2-t1）内从S1-S2位置移动到S′1-S′2位置，讨论在Δt时间内各种力对这段流体所做的功及由此引起的能量的变化。

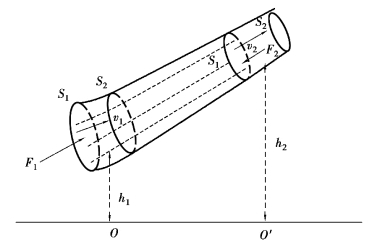
图4-10　伯努利方程的推导

1.压力所做的功

理想流体在流动时没有黏滞性；流管外侧面的流体对这段流体的压力方向垂直于流管表面，这个压力不做功；只有流管两端的流体对管内的流体压力才做功。由于Δt时间很短，从S1处到S′1处以及从S2处到S′2处的流体的压强、流速及流管的过流断面截面积、高度的变化都是很微小的。

作用在S1处的压力F1=p1S1为推力，所做的功为正功，即

A1=F1d1=F1v1Δt=p1S1v1Δt

作用在S2处的压力F2=p2S2为阻力，所做的功为负功，即(https://www.xing528.com)

A2=F2d2=F2v2Δt=p2S2v2Δt

在时间Δt内外力所做的净功为

A=A1-A2=p1S1v1Δt-p2S2v2Δt

式中，S1v1Δt和S2v2Δt分别等于包围在S1S′1和S2S′2之间的流体的体积。按流体连续性原理，它们是相等的，用体积V表示，且这两部分流体的质量也是相等的，以m表示流体的这一质量，则上式可写成

A=p1V-p2V

2.重力势能的增量

W=W2-W1=mgh2-mgh1

3.动能的增量

根据功能原理有

A=W+E

即

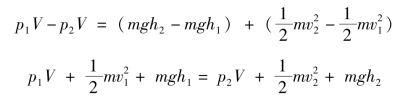
因流体段是任意选取的，故

式（4-1）是瑞士科学家伯努利于1738年首先导出来的，称为伯努利方程。方程式中pV具有能量的量纲，可把它看作体积为V的流体处于压强p之下所具有的能量，称为压强能。伯努利方程可叙述为：在重力作用下一定质量的理想流体做定常流动时，在流管的任一过流断面处，其动能、势能、压强能之和为一常量。将式（4-1）两边同时除以V，得

式中是流体的密度。式（4-2）是伯努利方程常用的表达式。该式说明，理想流体做定常流动时，在同一流管的任一过流断面处，单位体积流体的动能、势能、压强能之和是一个常量。一般地，对不同的流管，这个常量的值是不同的。伯努利方程是流体力学的基本定律之一。

伯努利方程是人体或器械在流体中进行技术分析的主要理论基础。假如流体在水平流管中流动时，即流体的高度不发生变化的情况下，伯努利方程可简化为

由式（4-3）可知，在同一水平管中流动的流体，流速小的地方压强大，流速大的地方压强小。

由连续性方程及伯努利方程，可以得出重要结论：理想液体在水平管中做定常流动时，压强和流速的关系为截面积大，则流速小，压强大；截面积小，则流速大，压强小。

（一）运动状态的等效原则及应用

运动状态的等效原则是指在流体中运动的物体与周围流体作用的等效性，即物体在流体中运动时受到流体作用力，与物体静止不动，流体以相同的运动作用于物体的作用等效。类似于运动的相对性。

运用运动状态的等效原则可以降低成本，提高工作效率。例如，利用风洞实验和水槽模拟飞行器在空气中及水中器械的运动。依据运动的相对性原理，将器械、实物或模型固定在人工环境中，人为制造气流或水流流过物体，以此模拟空中或水中各种复杂的运动状态，获取试验数据。简单地说，风洞就是在地面上人为地创造一个“空间”。实现运动训练或产品设计的“一天等于一个年”的效果。

（二）旋转球弧线运动分析——马格努斯效应

根据伯努利原理可知，当球体在流体中既有平动又有转动时，由于球表面不光滑性和流体的黏滞性，球体表面会附着一层空气随着球体一起转动，球体周围形成空气环流附着层[图4-11（a）]、[图4-11（b）]。当球顺时针方向转动同时以一定的速度向前运动时，球的右边环流与周围空气层流方向相同，球体右侧空气流动速度比不旋转时流速大，在球体的左侧由于空气环流和层流的方向相反，空气流动速度比不旋转时流速小。根据伯努利原理，流速大处压强小，流速小处压强大，球体右侧受到的压强小于左侧受到的压强，相当于受到一个由左方指向右方的力，从而使球的飞行轨迹向右发生偏转。这种现象称为马格努斯效应，即空气动力使旋转物体改变运动轨迹的效应。

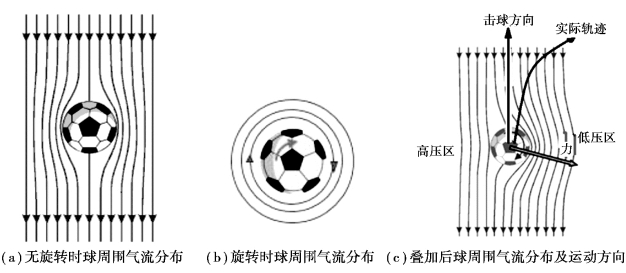
图4-11　不同情况的球在流体中产生的现象

体育运动中旋转球在空气中运动时，都会产生马格努斯效应，也称为罗宾斯效应。马格努斯效应在体育实践中应用十分广泛，如各种上旋球、下旋球及侧旋球的特殊轨迹，足球、排球、乒乓球、网球等都会出现马格努斯效应。其大小取决于物体运动的速度及旋转的速度、流体密度、球体质量、形状及球体表面的粗糙程度等。

（三）香蕉球的原理

香蕉球又称“弧线球”“弧旋球”，是足球运动中的技术名词，是指运动员运用脚法踢出球后并使球在空中向前做弧线运行轨迹的踢球技术。弧线球常用于攻方在对方禁区附近获得直接任意球时，利用其弧线运行状态，避开人墙直接射门得分。因其运动路线似香蕉形状，故称为“香蕉球”。

如图4-12所示，在足球比赛中，以右脚球员为例，主罚直接任意球的时候用右脚内侧向侧前方向踢球，足球向球门方向运动（以后以球门方向为前），同时脚内侧的摩擦使足球产生逆时针方向的旋转（自上向下俯视方向），由于空气具有一定的黏滞性，因此当球转动时，空气与球面发生摩擦，旋转着的球就带动周围的空气层一起同向转动，在足球旋转的带动下，足球周围也将产生和足球旋转方向一致的环流。又由于足球同时向前运动，因此相对于足球前进的方向，在足球飞行过程中周围空气气流产生相对于足球是向后的层流。这样在足球的左侧，旋转产生的环流和飞行中的层流方向相同，导致足球左侧空气流动速度加快；在足球的右侧，旋转产生的环流和飞行中的层流方向相反，使该侧气流流速变慢。根据流体力学的伯努利定理，在速度较大一侧的压强比速度较小一侧的压强小，球左侧受到的压强小于球右侧受到的压强。因为球所受空气压力的合力左右不等，总合力向左，所以球在运行过程中就产生了向左的运行，即产生弧线。

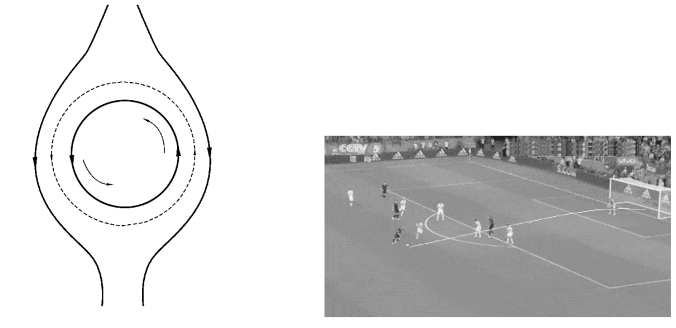
图4-12　香蕉球飞行轨迹的变化

至于旋转球在飞行一段时间以后突然出现的拐弯现象，是由于球在刚开始运动时，其平动速度较大，单位时间内其平动位移较大，旋转的压力差虽然不断改变着平动速度的方向，但相对于较高的平动运动的速度来说，它所引起运动轨迹弯曲度显得较小。而在球体运动末期，因平动速度的大幅度减小，而旋转的角速度减小较慢，故球体的偏转现象比较明显，宏观观察到的现象是，运动的轨迹体现出突然转弯的现象。这种空气作用效应在其他球类项目中也常见。

（四）乒乓球弧圈球的原理

以上旋球为例分析乒乓球在空气中运行轨迹（图4-13）。上旋球在空气中绕球的额状轴向前旋转飞行。这种上旋飞行的球落在台上之前，在马格努斯效应下乒乓球的上方受到的压强大于球的下方受到的压强，使飞行中的球过网后急促下降着台，落地点要比不旋转的球的落地点近。因为球体是旋转的，在与台面碰撞时，乒乓球相对台面有向后运动的趋势，乒乓球会受到台面给予的水平向前方向的冲量，从而使球获得一个水平速度的增量，所以乒乓球反弹后会形成强烈的前冲效果。乒乓球的反射角大于入射角，上旋球转速越快，所获得的水平速度增量就越大，反射角就越大；上旋球飞行的方向越平缓，即入射角越大，反射角也就越大。

图4-13　乒乓球上旋球轨迹变化

（五）排球飘球的原理

排球飘球是指不旋转、在空中飘晃飞行的球。主要见于发球之中，飘球在飞行中的飘晃性给对方运动员的判断带来了困难，增加接发球的难度，是常用发球技术之一。从现象上看，飘球在空中飞行的轨迹不是一条光滑的抛物线，类似周期摆动，或是以突然失速下吊的方式运动。从发球技术上来看，发飘球时，要使作用力通过球体重心，球不发生旋转。击球时手和球的接触面要小，发力突然、短促，手腕跟球的时间要短（图4-14）。

图4-14　排球扣球

飘球的形成是运动员大力击球，使球变形且不旋转快速飞行，由于球体表面粗糙不光滑附着一层空气，根据马格努斯效应的作用，再加上球的严重变形及排球质量较轻，使球飞行时四周受到的空气压力不均匀，形成的压强差位置变化不定，促使使排球脱离抛物线轨迹形成了飘浮不定的飘球。

历史事件人物

贝克汉姆

这也许是全欧洲最昂贵的右脚，擅长用内脚背主罚，足球以悦目的内旋弧线向对手的大门死角飞去。贝克汉姆从小接受科班训练，一招一式看上去非常朴实正统。为了提高速度，他必须扭摆全身，让身体完全倾斜来增大足球的内旋速度，通常给人以迅雷不及掩耳的感觉，这就是我们常见的贝氏任意球主罚姿势。门将总会纳闷为什么经常是判断准方向却仍然慢了半拍，科学数据告诉我们，小贝的每次任意球射门球速都在110 km/h以上，人们将他的旋转、快速、落点准确的弧线球称为“贝氏弧度”，在进攻上是简单却一击致命的有效武器。昔日任意球大师普拉蒂尼曾如此评价：“贝克汉姆肯定是欧洲最好的右脚任意球队员，如果不幸和他所效力的球队相遇，绝对不要在本方大禁区附近给他任何机会。”

经典回放：2002年世界杯预选赛，对希腊一战，最后一分钟，最激动人心的一脚，价值1亿英镑！作为当今世界头号球星，小罗的任意球速度与弧线结合得异常完美，在格雷米奥，在巴黎，在巴塞罗那，人们习惯了他用一次次精准的半高球羞辱对方门将。加入红蓝军团的第一年他以15粒进球帮助巴萨重回巅峰，并进而获得世界足球先生头衔。他在国家队的地位也直线上升，除非35 m开外，不然小罗基本包办了禁区前沿的所有定位球，其脚头之精准也得到各方好评。更可怕的是巴西天王罚任意球往往不用助跑，以小腿发力就能完成所有工序，让对方门将无从判断球路。在那场世纪大战中虽然球队落败，但小罗罚出的绕过人墙的任意球让西甲头号门神卡西利亚斯根本来不及反应。

罗纳尔迪尼奥

经典回放：2004年巴塞罗那主场与皇家社会一战，直到第90分钟巴萨还以0∶1落后，小罗自己博得了一个禁区前任意球，距离有点近，但巴西人射出的任意球依然直窜左下死角。整个诺坎普疯狂了，既为在积分榜上超越老对头皇马，也为他们新国王的降临而抑制不住内心倾泻而出的激动。其貌不扬的巴西小个子卡洛斯有着一个神奇的左脚，他上肢短小，大腿粗壮有力，小腿摆动幅度隐蔽而迅速，依托强大的爆发力量主罚任意球。对手们绝不敢在禁区外轻易地犯规，因为这个神奇小子主罚的任意球和被判罚点球几乎没区别。此外，卡洛斯好像也在学习桌球斯诺克的嫁接球原理，通过人墙中第三者碰撞而让足球改变方向打进球门有时让人觉得是他刻意计算出来的，他不需要费事去躲避“人墙”封堵而可以直接考验“靶子”的反弹力。那血脉偾张、霸气十足的任意球正是这袖珍金左脚称雄世界足坛的金字招牌。

罗伯特·卡洛斯

经典回放：1997年法国四国足球邀请赛上打入法国队球门的那个足以载入史册的40 m远石破天惊的外旋飞弹。赛后法国报纸因为无法解释卡洛斯是如何将那个飞向角旗的球变向打进球门，不得不以物理学角度调侃解释“根据牛顿第三定律，当某物体向右移动时，来自物体相斥的风速会对其起反作用。”里昂实现不可思议的联赛四连冠，小儒尼尼奥是当之无愧的最大功臣。自打加盟法甲班霸以来擅长严谨组织调度的他就蜕变为法兰西赛场首屈一指的中场艺术家。同时，这个巴西人还是顶尖的任意球大师，据统计其每七次主罚定位球就有一次绕过人墙旋入球门，这个概率是何等可怕。卡恩应该是最清楚巴西人厉害的一个，冠军联赛中德国门神就被小儒尼尼奥的任意球肆意羞辱。就连公认的顶尖定位球高手阿松桑和卡洛斯都曾坦然承认同胞的绝艺在自己之上。小儒尼尼奥的任意球绝技依赖于天赋和感觉还有苦练，一直以来，每次训练之后至少加练20个任意球已经成为他的固定习惯。虽然在国家队他还属于配角式的人物，但在崇尚技术足球的法兰西，他是绝对的王者至尊。

小儒尼尼奥

经典回放：冠军联赛中小儒尼尼奥35 m处的任意球直接攻破不莱梅门将莱因克把守的大门，堪称传世经典，被公认为上届冠军联赛最佳进球之一，媲美小罗打进切尔西，加西亚打进尤文的那两脚魔幻进球。左脚外脚背的任意球抽射是米哈的拿手好戏，在距离球门40 m内的直接任意球射门无懈可击。米哈的任意球势大力沉，是角度刁钻而且旋转强烈的结合完美的艺术品。其主罚任意球的时候通常会尽可能用小腿发力，大腿摆动幅度非常小，让守门员无从判断球路，故而神鬼莫测。“我们已经问过欧足联在米哈伊洛维奇罚任意球时我们是否可以用两名门将，我认为那是唯一阻挡他的方法。”当年勒沃库森在欧洲冠军联赛上和拉齐奥队分在同一小组时，该队功勋教练道姆自我解嘲说。“米哈”的任意球功夫独步欧陆足坛，是亚平宁赛场打入直接定位球纪录的保持者，甚至我们想到米哈几乎第一印象就是注册商标式的任意球，反之亦然，几乎成了条件反射，而其“弹不虚发”见血封喉的准头也让对手胆寒。

米哈伊洛维奇

经典回放：1999年，米哈伊洛维奇在对桑普多利亚队的比赛中以直接任意球连中三元，创造了前无古人、后也难有来者的历史性壮举。