深度学习的训练方法如今已经有了许多复杂的变种实现,但这些实现的基本思想都是相同的。
(一)自动编码器
深度学习的基本算法被称为逐层贪心算法,该算法在每一次迭代中训练一层网络,然后使用一个类似于后向传播的算法对深度网络进行调优。具体来说,首先将深度网络看成一连串的自动编码器。每个自动编码器可以看成由两个阶段构成,第一个阶段是编码阶段,编码阶段对应输入层到隐藏层的映射;第二个阶段是解码阶段,对应的是隐藏层到输出层的映射。自动编码器实现编码的学习过程如下:首先用隐藏层进行编码,再将编码结果作为输入传递给输出层进行解码,解码后的结果应该与原始输入相似但并不相同,通过将结果与原始输入的误差最小化得到最优编码方案,把中间层参数提取出来就是一个最优编码方案。
1.前向训练阶段
在逐层贪心算法中,我们在整体上将自动编码器拆开,编码过程用下面的公式表示:
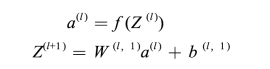
解码过程用下面的公式表示:
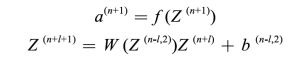
其中,a(n)就包含了我们想要的高阶特征。
一个更具体的含两个隐藏层的训练步骤如下。
(1)首先训练第一层自动编码器,如图3-3所示。
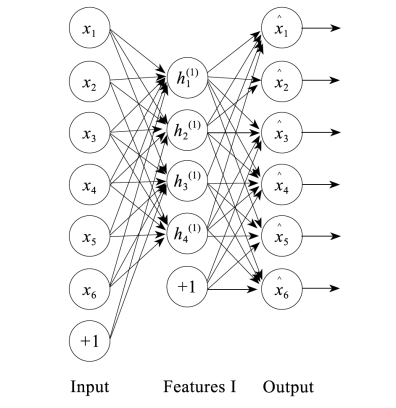
图3-3 自动编码器训练步骤1
然后将第一层自动编码器的解码部分拿掉,直接将第一层的编码结果作为输入,利用这个输入训练第二层编码器(图3-4)。
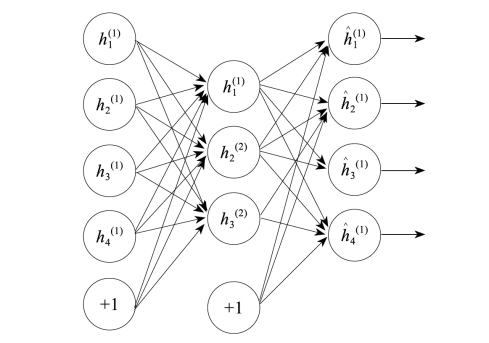
图3-4 自动编码器训练步骤2
(3)最后根据需要将第二层的解码部分换成相应的分类函数即可实现一个简单的分类器(图3-5)。

图3-4 自动编码器训练步骤3
2.后向调优阶段
后向调优阶段的调优过程如下。
(1)从输出层n1开始,计算参数:
![]()
(2)对于l=n1-1,n1-2,…,2层,计算参数:
![]()
(3)计算目标偏微分:
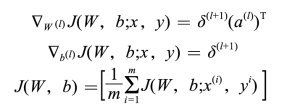 (https://www.xing528.com)
(https://www.xing528.com)
(4)使用偏微分对各参数进行更新:
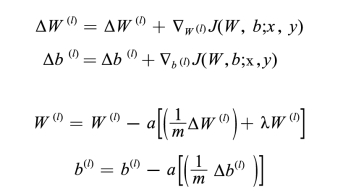
(5)完成更新后,即完成一次优化迭代。
(二)稀疏编码
如果把输出必须和输入相等的限制放松,同时利用线性代数中基的概念,可以得到这样一个优化问题:
min|I-O|
其中,I表示输入,O表示输出。
通过求解这个最优化式子,可以求得系数和基,这些系数和基就是输入的另外一种近似表达。
![]()
因此,它们可以用来表达输入I,这个过程也是自动学习得到的。如果在上述式子中加上L1的正则因子限制,则得到
min|I-O|+u×(|a1|+|a2|+...+|an|)
这种方法被称为稀疏编码(Sparse Coding)。通俗地说,就是将一个信号表示为一组基的线性组合,而且要求只需要较少的几个基就可以将信号表示出来。稀疏性定义为:只有很少的几个非零元素或只有很少的几个远大于零的元素。要求系数ai稀疏的意思就是:对于一组输入向量,只想有尽可能少的几个系数远大于零。选择使用具有稀疏性的分量来表示输入数据是有原因的,因为绝大多数的感官数据,比如自然图像,可以被表示成少量基本元素的叠加,在图像中这些基本元素可以是面或者线。同时,比如与初级视觉皮层的类比过程也因此得到了提升(人脑有大量的神经元,但对于某些图像或者边缘只有很少的神经元兴奋,其他都处于抑制状态)。
稀疏编码算法是一种无监督学习方法,它用来寻找一组“超完备”基向量以更高效地表示样本数据。虽然主成分分析技术(PCA)能使我们方便地找到一组“完备”基向量,但是这里我们想要做的是找到一组“超完备”基向量来表示输入向量(也就是说,基向量的个数比输入向量的维数要太)。超完备基的好处是它们能更有效地找出隐含在输入数据内部的结构与模式。然而,对于超完备基来说,系数ai不再由输入向量唯一确定。因此,在稀疏编码算法中,我们另加了一个评判标准“稀疏性”来解决因超完备而导致的退化(degeneracy)问题。稀疏编码算法可分为Training和Coding两个阶段。
1.Training阶段
给定一系列的样本图片[x1,x2,…],需要学习得到一组基[φ1,φ2,…],也就是字典。
稀疏编码是K-Means算法的变体,两者训练过程相差不多。由于K-Means聚类算法为EM算法的具体应用,EM算法的思想是,如果要优化的目标函数包含两个变量,如L(W,B),那么可以先固定W,调整B使得L最小,然后固定B,调整W使L最小,这样迭代交替,不断将L推向最小值。
稀疏编码的训练过程就是一个重复迭代的过程,按上面所说,交替地更改a和φ,使下面这个目标函数最小:
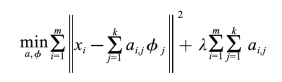
每次迭代分两步:
(1)固定字典φ[k],然后调整a[k],使得上式,即目标函数最小(即解LASSO问题)。
(2)然后固定a[k],调整φ[k],使得上式,即目标函数最小(即解凸QP问题)。
不断迭代,直至收敛。这样就可以得到一组可以良好表示这一系列x的基,也就是字典。
2.Coding阶段
给定一个新的图片x,由上面得到的字典,通过解一个LASSO问题得到稀疏向量a。这个稀疏向量就是这个输入向量x的一个稀疏表达。
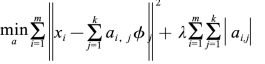
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




