基于Petri网的可重组制造系统建模、性能分析

制造系统重组生产方式与其他混流生产方式（如：基于精益生产的“拉式”混流生产方式）相比，不同之处在于：前者的重组主要包括了物理构件重组，系统重组依赖于具有可重组功能的设备支持；后者是通过生产管理流程的变化实现不同产品的混流生产。可重组制造系统建模及性能分析步骤如下。

1.建立ESPN模型

设电机转子生产线的8道工位缓冲及存储输入输出能力足够大。当原材料空闲，由运输设备将其从存储缓冲区送至第一道加工工位，如加工设备处于空闲状态则开始加工工件，加工结束后，如输出缓冲空闲，输送至输出缓冲由运输设备运送到下一个工位，等待被加工，运输工具采用小车，每台小车为320个汽车电机。该生产线的ESPN模型如图3-6所示，各变迁含义及特性见表3-5。

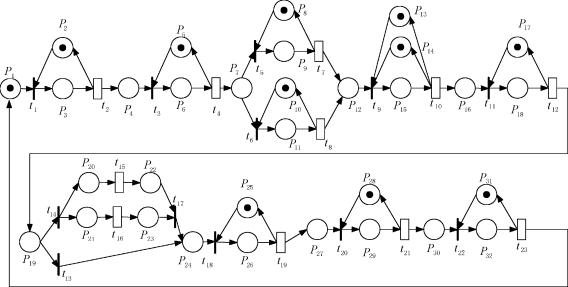
图3-6　可重组电机生产线ESPN模型

模型中主要变量的定义：

●θ为不同产品的混流比。第三道工位中由于要加工产品的不同，使用的加工设备不同（分别为插绝缘机和涂敷机）。θ为原材料分配给插绝缘机（即t5）概率，相应的分配给涂敷机（即t6）概率为（1-θ）。

●x为瓶颈工位的加工周期，单台设备加工为x，加上一台可移动加工设备加工周期变为x/2，加上两台可移动加工设备则加工周期变为x/3，以此类推。

表3-5　图3-6中各变迁的特性说明

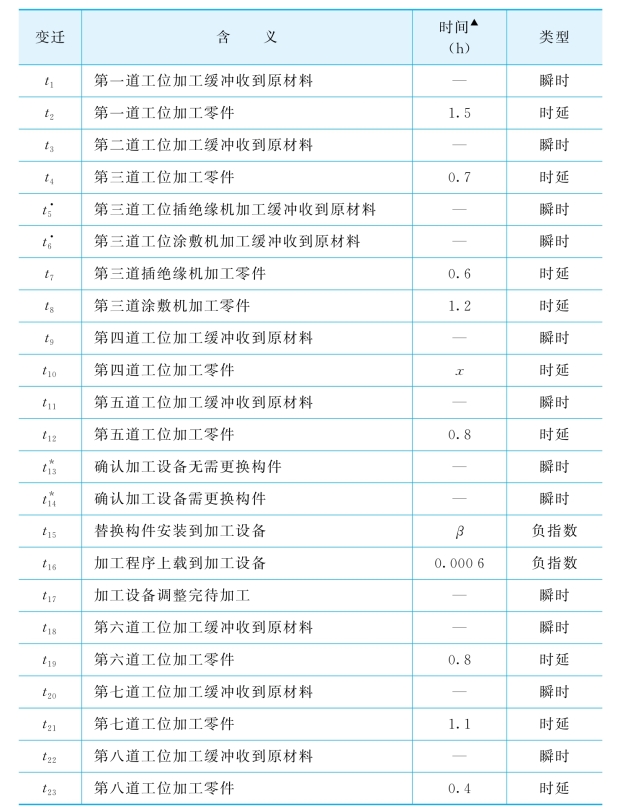
注：▲加工变迁的时间为每辆运输小车上所有零件的加工时间；
＊按工厂实际情况测得：t14激发概率为1/5，t13的激发概率为4/5；
●设t5激发概率为θ，t6的激发概率为1-θ

●β为第六道工位中加工设备需要调整内部构件实现重构的平均Rump-up时间。该Rump-up时间经实际测量符合负指数分布。

模型中的各工位加工时间及相关参数由实际生产过程测得[145]。

2.基于行为表达式的计算

利用Petri网的简化原则（图3-2），按照ESPN的基于行为表达式的分析方法，得到总的周期表达式为：

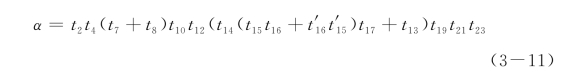
该行为表达式代表了一个电机从进入生产线开始加工一直到加工完最后一道工序的全部过程。式（3-11）中的传递函数为：

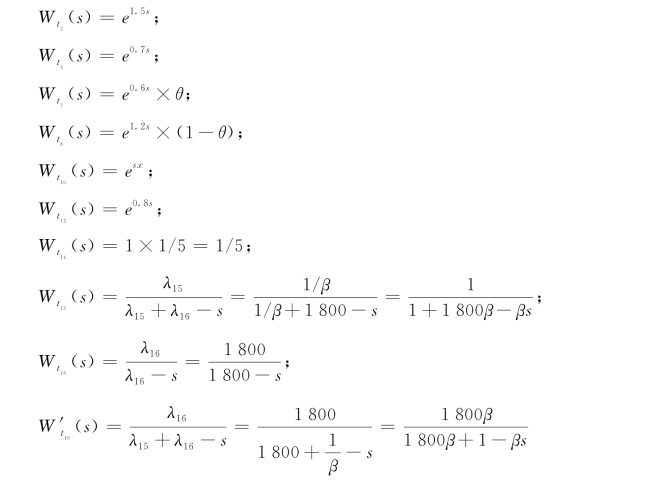
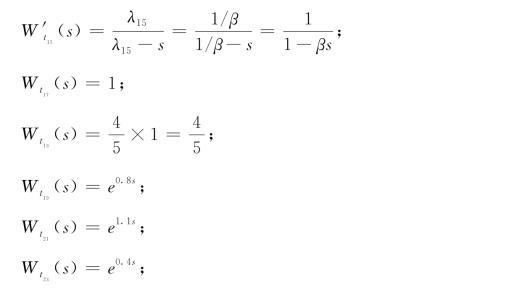
根据定理3.1～3.3计算α的传递函数：Wα（s）=e1.3Se0.7s（θe0.6s+（1-θ）e1.2s）esxe0.8s（1/5（（1/（1+1 800β-βθ））（1 800/（1 800-s））+（1 800β/（1+1 800β-βθ）（1/（1-βθ））+4/5）e0.8se1.1se0.4s。

可得到完成一个产品的生产周期为：

由式（3-12）可知生产周期是关于θ，x，β的一个函数。得到这个函数后，就可以根据具体的系统性能指标进行性能分析。

3.系统性能分析

基于上述生产周期函数，可以得到以下性能指标：

●稳定概率

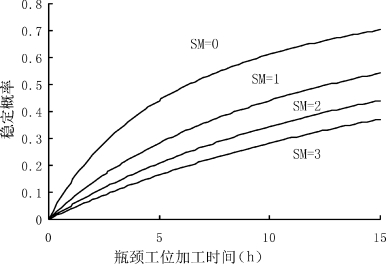
稳定概率表明了生产过程中处于某一状态的概率。在可重组生产线中，最受关注的是系统处在瓶颈工位加工状态的稳定概率（图3-7）与系统处在可重组调整状态（Rump-up时间）的稳定概率（图3-8）。

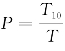零件的生产周期中，为考察瓶颈工位t10对生产过程的影响，令Wi（s）中的s=0，其中i是除t10之外的所有时间变迁，从而得到该状态的传递函数Wα（s）=esx，因此，；则处于瓶颈工位加工状态的稳定概率是。按生产实际情况，以x为变量，式3-12中β，θ参数分别取θ=0.6，β=1，得到瓶颈工位加工状态的稳定概率（图3-7）。同理，系统处在Rump-up调整状态的稳定概率（图3-8）。

(www.xing528.com)

图3-7　瓶颈工位加工状态的稳定概率

注：SM表示可移动加工设备

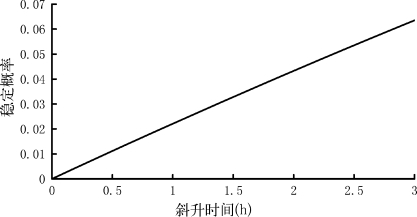
图3-8　Rump-up调整状态的稳定概率

●生产率

生产率是衡量一个生产过程是否高效的标准。可重组制造系统中，影响系统生产率的因素除了制造系统常见的瓶颈工位加工时间外，还包括可移动加工设备的台数对生产率的影响、系统Rump-up时间对生产率以及混流比对生产率的影响程度。这三项标准既是判断可重组制造系统效率的标准之一，也为规划、配置可重组制造系统提供基础数据。

①可移动加工设备对生产率的影响

式（3-12）中，取θ=0.6，β=1，可得T=6.34+x。图3-9表明可移动加工设备和生产率的关系。

由图3-9可知，随着可移动加工设备的增加，生产率得到明显的提高；但是，当可移动加工设备的引入有效地消除了瓶颈工位对生产的制约，则生产率的提高将是有限的，并且接近一个上限。

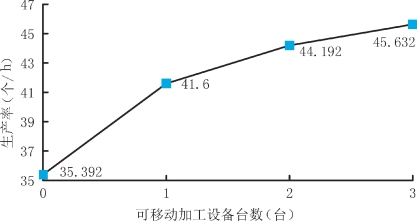
图3-9　可移动加工设备对生产率的影响

注：实际生产过程中，当可移动加工设备为1台时，生产率为41，与图中计算结果基本吻合。实际生产率因废品、人员等因素要比计算值略低。

②瓶颈工位加工节拍对生产率的影响

式（3-12）中，取θ=0.6，β=1，可得（n是可移动加工设备台数）。图3-10表明瓶颈工位加工节拍和生产率的关系，由图3-10可知，随着瓶颈工位耗时的延长，生产率的降低快慢程度将随着瓶颈工位的加工能力不同而不同，加工能力低则生产率下降迅速，加工能力高则生产率下降缓慢。因此，在设计或更改系统时，可根据具体生产系统并参考图3-9和图3-10，设计最佳的增加/移走可移动加工设备的方案。

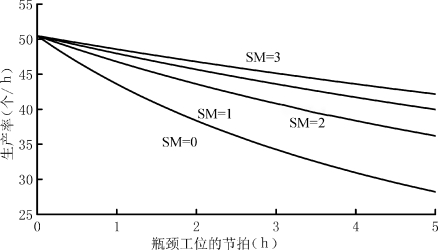
图3-10　瓶颈工位节拍对生产率的影响

注：实际生产过程中，当可移动加工设备为零台，瓶颈工位耗时2.7时，生产率为35

③Rump-up时间对生产率的影响

式（3-12）中，取θ=0.6，x=2.7（单台设备），可得T=8.84+β/5（1+1 800β）2+（360/（1+1 800β））（1/1 8002+β2）。图3-11表明系统Rump-up时间和生产率的关系。由图3-11可知，随着Rump-up时间的延长，产品加工周期加长，生产率降低。在实际设计可重组制造系统时，应测算Rump-up时间，有助于准确计算系统生产率，并力争在系统运行过程中有效降低Rump-up时间。

④混流比对生产率的影响

式（3-12）中，取x=2.7，β=1（单台设备），可得T=9.4-0.6θ。图3-12表明混流比和生产率的关系。A，B两种不同产品需要经过不同的加工工序（图3-6中的第三道工序）或对同一工序进行构件重组进行生产（图3-6中的第六道工序）。由图3-12可知，最大的生产率在混流比最大处获得。

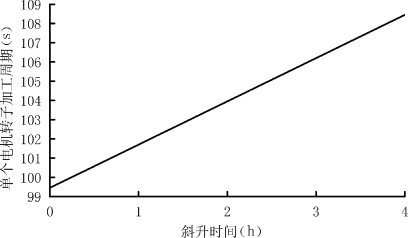
图3-11　Rump-up时间对生产率的影响

注：实际生产过程中，当Rump-up时间为1小时2分时，加工周期为102.7

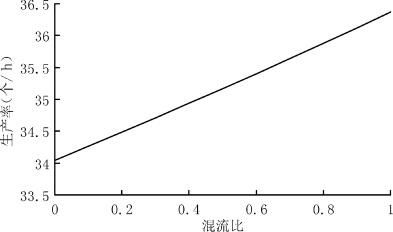
图3-12　混流比对生产率的影响

注：实际生产过程中，当混流比为0.6时，生产率为35台