基于Petri网的可重组制造系统研究

ESPN可以分析与Petri网相同的逻辑结构和性能指标，但是如果采用可达图的分析方法将会导致状态空间爆炸的问题。为避免系统可达图爆炸，本书引入了基于行为表达式的分析方法。

制造系统Petri网模型的行为表达式反映了制造系统的产品加工过程。根据行为表达式可以求得Petri网的传递函数，从而可以利用矩母函数思想，实现对扩展随机Petri网的性能分析。

1.矩母函数与传递函数

定义3.7[76，144] 设x是一个随机变量，则esx的期望值称为x的矩母函数，记为MGF（s）=E（esx）（x为实变数）。

若x为离散变量，具有概率分布函数p（xi）=P（X=xi），i=1，2，…，则矩母函数MGF（s）=。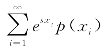

若x为连续随机变量，且概率密度函数为f（x），则x的矩母函数。

定义3.8[76，144] 在一个任意分布的随机Petri网中，对于M∈R（M0），t∈T，令Wt（s）=pM，tMGFM，t（s），则Wt（s）为t在M下的传递函数。其中pM，t为M下t被引发的概率，MGFM，t（s）为M下t的矩母函数。

2.基于行为表达式的分析方法

一个行为表达式或者是一个复合式，或者是一个幂级式。它可以描述有界Petri网，或者某些无界Petri网（表达式存在的Petri网）。根据表达式并借助下面几个定理，可以求得Petri网的传递函数W，再利用矩母函数的相关分析方法便可对任意分布的随机Petri网进行品质分析[144]。

定理3.1 设α是一个单项式，α=t1，t2，…，tq，则Wα（s）=。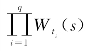

定理3.2 设α是一个标准多项式，α=α1+α2+，…，+αn，则W（s）=。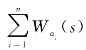

定理3.3 设α=（α）*，则Wα（s）=。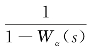

3.基于ESPN的可重组制造系统模型的分析方法及其步骤

基于行为表达式的分析方法一般为：建立系统的Petri网模型、给出系统的行为表达式、计算行为表达式的传递函数以及采用矩母函数相关方法进行性能指标的计算。对应到可重组制造系统的ESPN模型分析，具体步骤如下：(https://www.xing528.com)

（1）建立ESPN模型

给出不同加工设备的ESPN模块，并结合运输设备模块和仓储设备模块建立完整的可重组制造系统ESPN模型。

（2）构造系统行为表达式

产生系统的行为表达式，并将多项式化为标准多项式形式。系统的行为表达式对应了机械加工开始到加工结束的全部过程。

（3）求传递函数

根据所给的分布参数以及行为表达式结构，求出各事件的引发概率及其矩母函数，再根据传递函数定义得到各事件的传递函数。表达式中不同位置的同一事件的引发概率可能不一样。

（4）重新标号行为表达式

根据第三步的计算结果，为行为表达式重新标号，以区别表示式中具有不同传递函数的同一事件。如图3-4中由于上载加工程序与安装新构件存在并发性，替换构件安装到加工设备这个一事件（t3）在上载加工程序（t4）的前或后发生分别对应了不同的传递函数。

（5）重新计算传递函数

根据3.2.3节定理3.1～3.3计算标号后的行为表达式的传递函数。

（6）计算系统性能

基于前面的结果和矩母函数的有关方法进行各性能指标的计算，从而获得系统的定量分析结果。更重要的是，采用基于行为表达式的分析方法得到的是关于不同变量之间的函数关系，这为系统性能分析提供了很大的便利。