爆炸理论：冲击波基本性质解析

前已述及，冲击波是一种强压缩波，它具有如下特点。

（1）冲击波阵面通过前、后介质的参数是突跃变化的，即很薄的冲击波阵面两侧介质参数相差的值不是一个微分量，而是一个有限量。

（2）由于冲击波具有如上特性，可以推论：冲击波的传播过程虽然是绝热的，但却不是等熵的。可以证明冲击波传过后介质的熵是增加的，推证方法如下。

从式（2-2-19）知，对于冲击波的传播过程，有

两边积分后得到

由于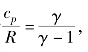则

又由于

则

将冲击波的兰金-雨果尼奥关系

代入式（2-6-2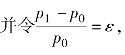），称为冲击波强度，整理可得

对于较弱的冲击波，ε是一个很微小的量，都小于1，按照对数展开：

将式（2-6-4）代入式（2-6-3），整理后得到

由于冲击波为压缩波，（p1-p0）＞0，γ＞1，故冲击波阵面通过前、后介质的熵变ΔS＝S1-S0＞0。另外，式（2-6-5）还表明，弱的平面正冲击波传过后，介质的熵值变化与对比参数的三次方，即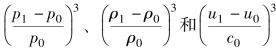成正比例关系。

以上论证虽然是对于多方气体中的冲击波进行的，但其结论在各种介质中普遍适用。

（3）冲击波的传播速度与介质的初始状态及冲击波强度相关。

根据式（2-5-25）可知

将ε引入上式，则(www.xing528.com)

上式可写为D＝f（c0，u0，ε），所以冲击波的传播速度与介质的初始状态及冲击波强度相关。

（4）冲击波的传播速度相对于未扰动介质而言是超声速的，即D＞u0+c0，若u0＝0，则D＞c0。

因为p1-p0＞0，由式（2-5-25）可得

因此有

故D-u0＞c0。

（5）冲击波的传播速度相对于波阵面后已受扰动的介质而言是亚声速的，即Du1＜c1。

由式（2-5-1）和声速表达式（2-3-9）可得

将上式和式（2-5-22）代入式（2-6-6），可得

对于冲击波来说，＞1且γ＞1，所以

故D-u1＜c1。

因此，冲击波相对于波阵面后已受扰动的介质而言，D＜u1+c1是成立的。

（6）冲击波传播介质获得了一个与传播方向相同的速度增量，即u1-u0＞0，且u1-u0＜D-u0。

由式（2-5-26）可知

或

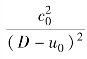观察上式，右边γ＞1，＜1，由　（4）　可知D-u0＞c0，所以，1＞1-＞0。

因此，u1-u0＞0，且u1-u0＜D-u0。