振幅特征曲线及无阻尼系统的激振频率

式 （15-33）反映出强迫振动振幅b的变化规律，引入

则强迫振动的振幅与b0 的比值（动力放大系数）

为了清楚地表达强迫振动的振幅与其他因素的关系，我们将不同阻尼条件下的动力放大系数（反映振幅大小的无量纲量）β和频率比 （反映频率大小的无量纲量）的关系用曲线绘制出来，称为幅频特性曲线，如图15-15所示，由图可见：

（1）当ω≪ωn 时，β→1，阻尼对振幅的影响很小，可忽略阻尼的存在，看做无阻尼受迫振动。即振动方程为

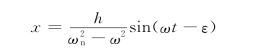
（2）当ω→ωn，即（λ→1）时，振幅显著增大。现求振幅取得极大值时的激振频率。对[（1-λ2）2+4ξ2λ2]求一阶导数，在一阶导数等于零时β存在极值，即

(www.xing528.com)

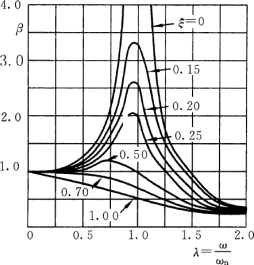
图15-15

可见，当ω在附近时，强迫振动的振幅显著增大，这一现象称为共振。此时的ω称为共振频率。阻尼对共振振幅的影响明显。当无阻尼时，βmax→∞，振动时振幅将逐渐增大；当ξ≥0．707时，将不发生共振现象；当0＜ξ＜0．707时，随着ξ的增大，振幅将逐渐减小，通常0．85＜λ＜1．15为共振区。

一般情况下，阻尼比ξ≪1，这时可以认为共振频率ω=ωn，即激振力频率等于系统固有频率时，系统发生共振，此时共振的振幅为

（3）当ω≫ωn时，λ→∞，β→0。即这时强迫振动的振幅很小。阻尼对振幅的影响也很小，可以忽略阻尼，又将系统当作无阻尼系统处理。

回转机械，如电动、涡轮机等在运转时经常发生振动。当转速在某一特定值时，振幅会显著增大。而转速偏离此特定值时，振幅又会很快减小。这是由于这一特定转速对应着系统的固有频率，常称这一转速为转子的临界转速。所以，一般情况下，转子不允许在临界转速下运转，只能在远低于或远高于临界转速时运转。