阻尼对自由振动的影响及其衰减振动效果

前两节所讲的自由振动，在理论上能永远继续下去，其振幅也始终保持不变，但实际观察到的自由振动其振幅总是逐渐衰减，直至最终振动停止。这种理论与实际的矛盾是由于前面研究振动时均忽略了阻力这一因素，而阻力的存在，不断消耗着振动的能量。因此有必要研究一下阻力对自由振动的影响。

振动过程中的阻力习惯上称为阻尼。产生阻尼的原因很多，例如物体在介质中振动时的介质阻尼、结构材料变形而产生的结构阻尼和干摩擦阻尼等。当振动速度不大时，介质阻尼近似与速度的一次方成正比，这样的阻尼称为黏性阻尼。如果设物体的速度为v，则黏性阻尼力

式中：c为黏性阻尼系数，它的大小与物体的形状、大小和介质性质有关，单位为kg/s；负号表示黏性阻尼力的方向与速度方向相反。阻尼常用图15-12 （a）中所示的阻尼元件c表示。一般的机械振动系统均可简化为由惯性元件m、弹性元件k和阻尼元件c组成的系统。

现建立由图15-12所示单自由度有阻尼系统自由振动微分方程。仍取静平衡位置为坐标原点，当重物偏离原点x坐标时，重物受到重力、弹性力和阻尼力作用，与无阻尼系统一样，重力与弹性力的初始值相平衡，故可不出现在方程中，则其受力如图15-12（b）所示，其中

图15-12

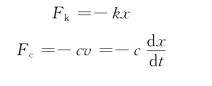(www.xing528.com)

则物块运动微分方程为

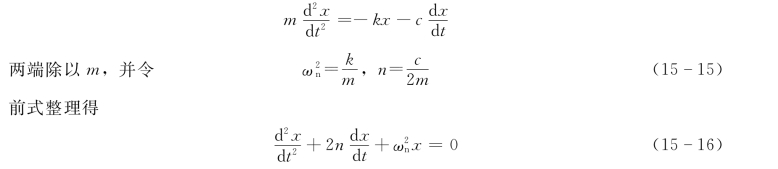
式 （15-16）称为有阻尼自由振动微分方程的标准形式，它仍是一个二阶常系数齐次线性微分方程，它的特征方程为

特征方程的根为

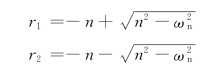
随着阻尼大小的不同，特征根有实数和复数之别，运动规律也有很大不同。现分不同情况加以讨论。