其他类型单自由度振动系统分析

工程实际中除了 “质量—弹簧”振动系统外，还有很多其他类型的振动系统，如扭振系统、摆振系统等。这些系统形式上虽然不同，但它们却具有相同的运动微分方程形式。

图15-7为一扭振系统。其中扭杆一端固定，另一端与一圆盘刚性固连。设扭杆上、下端面相对转过单位扭角时产生的扭转力矩为k，则k称为扭转刚度系数。当扭杆上下端面相对转过φ角时，产生的扭转力偶矩为Mf=kφ，方向与φ角转向相反。圆盘对中心轴的转动惯量为JO，则圆盘绕中心轴的转动微分方程为

图15-7

可见此式与式（15-4）相同。因此研究“质量—弹簧”系统的振动具有普遍的物理意义。

图15-8

【例15-2】 重物P自高h=1m处自由落在水平梁的中部。设重物在碰到梁后即与梁连在一起上下振动，求其自由振动的规律。已知当物体静止在梁中部时，梁有静变形δst=0．001m，梁重不计。

解：由重物和弹性梁组成的振动系统，与图15-2所示系统完全相似，因无其他外力作用，故系统为自由振动。

将坐标原点取在振动系统的静平衡位置上，x轴铅直向下，如图15-8所示。振动的固有频率由式（15-10）可得

物块的运动方程为

取重物刚落到梁上时为初瞬时，则初始条件为x0=-0．001m，代入式（15-11），求得振幅A和初相位α为

所以，物块的自由振动规律为x=0．0447sin （99t+0．0223）m。

【例15-3】 图15-9为一摆振系统，杆重不计，小球质量为m，摆对轴O的转动惯量为JO，弹簧刚度为k。设杆在水平位置平衡时，其余尺寸如图所示。求此系统微小振动的运动微分方程及固有频率。

解：当摆在水平位置平衡时，弹簧的压缩量为δ0，列平衡方程∑mO（Fi）=0，有

当摆从平衡位置顺时针转动微小角度φ时，弹簧的压缩量为δ0+φd。列摆绕O轴的定轴转动微分方程

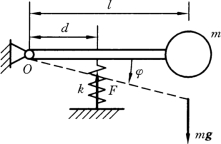
图15-9(www.xing528.com)

注意到上面的平衡关系，则上式化为

移项，化为标准形式的无阻尼自由振动微分方程得

则此摆振系统微幅振动时的固有频率为

【例15-4】 如图15-10所示轮轴的质量为m，轴的半径为r，对其质心O的回转半径为ρ0，放在半径为R的圆槽中只滚不滑地作微幅摆动。试求轮轴在微幅摆动时的固有频率。

解：以系统处于静平衡位置时为坐标原点，此时φ=0。轮轴作平面运动。取轮轴为研究对象，当转过微小角度φ时，其受力情况如图15-10所示。列轮轴的平面运动微分方程为

由运动学关系可知，质心O的轨迹是以O1 为圆心的圆周，其加速度为

图15-10

因为轮轴只滚不滑，故轮轴转动的角加速度为

由式（a）及式（d）求得摩擦力

将式（f）和式（g）及JO=m代入式（c）中，得

当轮轴微幅摆动时，sinφ≈φ，代入上式并化为标准形式有

故从上式可知，轮轴微幅摆动时的固有频率为