振动系统力学模型简化，理论力学

工程中的振动系统往往是很复杂的，为了研究振动系统的特性，必须将它简化为某种较简单的理想化的力学模型。最常见的简化方法是将系统简化为若干个由“无质量”的弹簧和 “无弹性”的质量所组成的 “质量—弹簧”系统。当振动系统仅有一个 “质量—弹簧”构成时，其质量块的空间位置由一个独立坐标确定，这是最简单的振动力学模型，如图15-1所示。这种由一个独立坐标就能确定振动系统的运动的系统称为单自由度振动系统。

工程中许多问题可简化为 “质量—弹簧”振动系统。图15-2 （a）为电机在梁上振动的系统，当研究电机随梁的变形而产生的上下振动时，如果电机质量远远大于梁的质量，则可视电机为无弹性、只有质量的质点，视梁为无质量、只有弹性的弹簧，其力学模型可简化为图15-2 （b）所示的“质量—弹簧”系统。

图15-3为汽车及其振动力学模型。在振动中，如果侧向和水平方向振动都很小时，

可认为汽车只在铅垂面内振动，则汽车的车体可看成平板，车架前后用弹簧支撑，形成由平板的重心C的铅垂坐标y 和相对重心C 的转角θ两个独立坐标确定的振动系统，这个系统称为二自由度系统。如果考虑汽车其他方向的振动或车桥、车胎等结构，汽车振动系统可简化为更多自由度的振动系统。可见，任何振动系统都可以根据具体情况，简化为一个自由度或多个自由度系统。

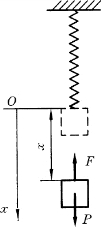
图15-1

图15-2

图15-3

【例15-1】 求图15-4所示串联弹簧和并联弹簧系统的等效弹簧刚度。设两弹簧刚度为k1和k2。

解：弹簧等效是指在相同力作用下，弹簧产生的静变形相等的两个弹簧或两组弹簧。现用图15-4 （c）单个弹簧分别等效图15-4 （a）和图15-4 （b）的两弹簧串联和并联系统。

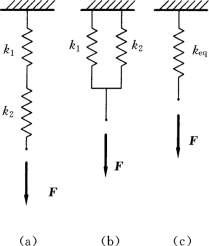
图15-4

（1）两弹簧串联。原系统在力F作用下，产生的静变形等于力F作用下两弹簧分别产生的静变形之和，即

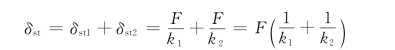(www.xing528.com)

对于等效弹簧系统，由力F产生的静变形为

两系统等效，则δst=δ′st，即

等效刚度

（2）两弹簧并联。原系统在力F作用下产生的静变形即为两弹簧各自产生的静变形，而两弹簧受到的拉力之和等于F，即

可见

等效弹簧在力F作用下的静变形为

两弹簧系统等效，故δst=δ′st，则有

以上分析方法均可推广到其他组合弹簧的等效刚度计算中。