求解虚位移原理-理论力学摘要

虚位移原理：具有理想约束的质点系其平衡的必要与充分条件，是作用在质点系上的所有主动力在任何虚位移中所作的虚功之和等于零。

如果作用于质点系中任一质点Mi上的主动力为Fi，约束反力为FNi，给定虚位移为δri，则

式 （14-6）的解析式为

虚位移原理由拉格朗日于1764年提出的，又称为虚功原理，它是研究一般质点系平衡的普遍定理，也称静力学普遍定理。

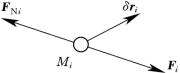
图14-7

（1）必要性证明：

当质点系平衡时，质点系中的每个质点受到主动力Fi 和约束力FNi而处于平衡，取质点系中任一质点Mi，如图14-7所示，则对作用在该质点上的主动力合力和约束反力合力FNi，应有

任意给质点系一组虚位移，其中质点Mi的虚位移为δri，则Fi和FNi所作虚功之和必等于零，即

对其他质点也可写出这样一个等式，将所有等式相加，有

由于质点系的约束都是理想约束，由式（14-5）可知

则有

（2）充分性证明：（略）。

【例14-1】 如图14-8所示机构，摇杆OB长l，杆重、滑块重不计，忽略摩擦，求在图示位置平衡时主动力F1 和F2 之间的关系。

解：（1）取系统为研究对象。

（2）受力分析。作用在机构上的主动力有F1和F2。

（3）运动分析。求虚位移间的关系。首先给滑块A以虚位移δrA，水平向左，B点虚位移δrB 如图14-8所示。求解虚位移之间的关系用几何法。

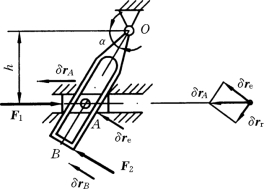
图14-8

按点的合成运动的速度分析，A、B两点的虚位移之间有如下关系

摇杆上A、B两点的虚位移关系

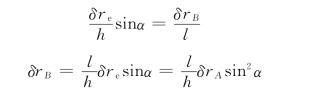
（4）列虚功方程，求解，即

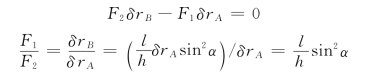
【例14-2】 曲柄连杆机构如图14-9所示，设水平力F1 作用在滑块B上，在曲柄销A上作用了阻力F2，方向垂直于OA。求曲柄连杆机构的平衡条件。

解：（1）取系统为研究对象。

（2）受力分析。作用在机构上的主动力有F1和F2。

（3）运动分析。求虚位移间的关系。首先给A点虚位移δrA 向上，则B点虚位移δrB 一定向左，如图14-9所示。求解虚位移之间的关系仍应用几何法。(www.xing528.com)

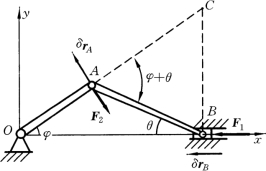
图14-9

连杆AB瞬心C的位置如图14-9所示，A、B两点的速度有

由图14-9可知，∠ABC=90°-θ，∠CAB=φ+θ，应用正弦定理得

（4）列虚功方程，求解，即

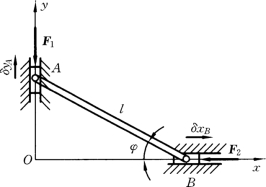
图14-10

以上两例是应用虚功方程式（14-6）和求解虚位移之间关系的几何法求解的。但有些问题应用几何法求虚位移之间的关系并不方便。在此情况下，可首先写出系统的约束方程或把各质点的坐标表示成参数形式，然后进行变分计算，确定虚位移关系，最后代入方程式（14-7）求解。

【例14-3】 如图14-10所示的椭圆规机构，连杆AB长l，杆重和滑道、铰链上的摩擦忽略不计。求

机构在图示位置平衡时主动力F1 和F2 之间的关系。解：（1）取系统为研究对象。

（2）受力分析。在应用式（14-7）时，式中Fix、Fiy、Fiz是各主动力在坐标上的投影，在本题中

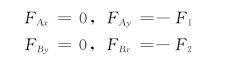
（3）运动分析。求虚位移间的关系。式 （14-7）中的δxi、δyi、δzi是主动力作用点位置坐标的变分，它们均按坐标的正方向，如图14-10所示。求解虚位移之间的关系可用两种方法：

1）利用对约束方程的变分求解，坐标xB，yA 得

对两边变分（与微分类似），得

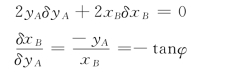
2）利用φ角求解，可知

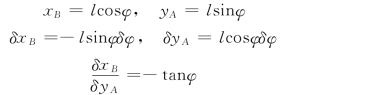
（4）列虚功方程（14-7）。求解

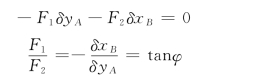
【例14-4】 如图14-11 （a）所示，求组合梁支座A约束反力。

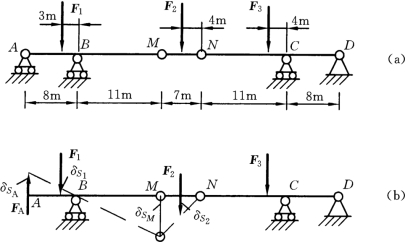
图14-11

解：将支座A处的约束解除，用力FA 代替，如图14-11 （b）所示。给该系统以虚位移，并建立虚功方程

其中

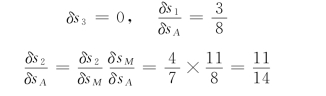
代入虚功方程，得

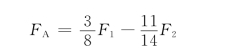
应该指出，式 （14-6）和式（14-7）为虚位移原理的两种不同的表达式。解题时，应用何种形式的虚功方程，要视具体情况而定。