设刚体具有质量对称平面且在平行于此平面内运动,则刚体的惯性力系可简化为在对称面内的平面力系。
取对称面为平面图形,如图13-5所示,由运动学知,平面图形的运动可分解为随基点的平动与绕基点的转动。取质心C为基点,设质心C的加速度为aC,刚体的转动角加速度为α。以质心C为简化中心,则惯性力系的主矢与主矩分别为
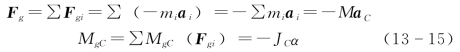
式中:JC 为刚体通过质心C轴的转动惯量。
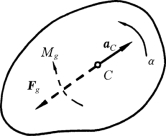
图13-5
以上结果表明:对于有对称面的刚体,平行于这一平面作平面运动时,其惯性力系可简化为一个过质心C点的力和一个作用在其对称面内的力偶,这个力大小等于刚体质量与质心加速度的乘积,其方向与质心加速度方向相反;这个力偶的力偶矩大小等于对通过质心C点且垂直于对称面的轴的转动惯量与角加速度的乘积,其转向与角加速度的转向相反。
【例13-1】 有一圆锥摆,如图13-6所示,重量P=9.8N的小球系于长l=30cm的绳上,绳的另一端则系在固定点O,并与铅直线成α=60°角。如小球在水平面内作匀速圆周运动,求小球的速度v及绳的张力T的大小。
解:以重物为研究的质点,在质点上除作用有重力P和绳拉力T外,加上法向惯性力 ,则其大小为
,则其大小为
![]()
根据达朗伯原理,这三个力在形式上组成平衡力系,即
![]()
取上式在自然轴上的投影式有
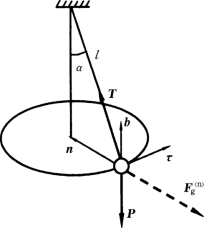
图13-6
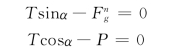
则
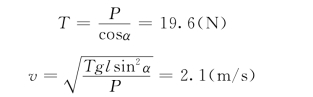
【例13-2】 桥式起重机的桥梁质量为m3=1000kg,吊车质量为5000kg,吊车吊一个质量为m1=2000kg的重物下放,如图13-7所示。吊车刹车时重物的加速度为a=0.5m/s2,求此时A、B处的约束反力(吊车所处的位置如图13-7所示)。
解:取桥梁、吊车、重物组成的系统为研究对象,其中只有重物为不平衡物体 (有加速度)。为了用达朗伯原理来进行计算,应先在重物上附加上它的惯性力,其方向与a相反,大小为
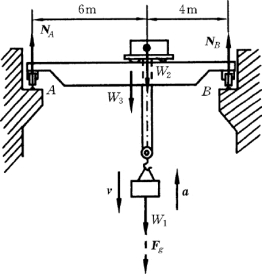
图13-7
![]()
然后将整个系统所受的主动力W1、W2、W3,约束反力NA、NB 和惯性力Fg 组成的力系看作平衡力系,用静力学平衡方程求解。(https://www.xing528.com)
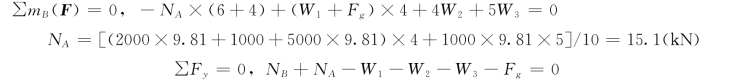
则 NB= (W1+W2+W3+Fg)-NA=3500×9.81+1000-15100=20200N=2.02 (kN)
【例13-3】 如图13-8所示,电动机的定子重P,安装在水平的基础上;转子重Q,其质心为C,偏心距OC=e,运动开始时重心C在最低位置。今转子以匀角速度ω转动,求电机所受的约束反力。
解:以电机整体为研究对象。除受重力P和Q外,基础及地脚螺钉对电机作用的约束反力向点A简化为一力偶M 与一力N (图中Nx 和Ny 为其分力)。对质点系加惯性力,转子绕定轴O以角速度ω匀速转动,惯性力系简化为一个通过O点的力,大小为Fg=Qeω2/g。其方向与质心C的加速度aC 相反。
根据达朗伯原理,作用于质点系的主动力、约束反力与惯性力在形式上组成平衡力系,可列出平衡方程,即
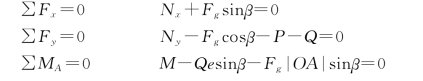
因转子匀速转动,β=ωt,代入上述方程组中得
![]()
解得
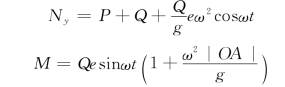
【例13-4】 重为G半径为r的均质圆球沿倾角是θ的斜面无初速地滚下,如图13-9所示。欲使球滚而不滑,摩擦系数f最小应等于多少?

根据达朗伯原理列出平衡方程
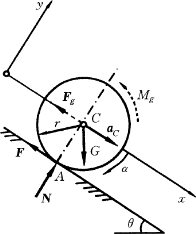
图13-9

联立以上三式求得
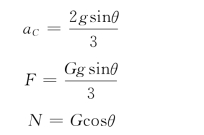
要使球滚而不滑,应有F≤fN,即
![]()
式中:f为静摩擦系数。则
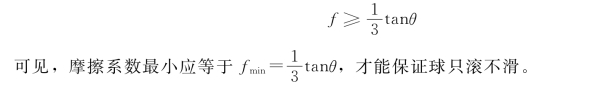
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




