动力学普遍定理包括动量定理、动量矩定理和动能定理这三大部分内容,有关这些定理及其单独应用已在前面有关章节分别进行了讨论,但是有许多动力学问题,特别是比较复杂的综合性问题,往往不是应用某个定理所能解决的,需要联合应用几个定理才能求解。而且一个问题往往有几种求解方法,所以如何综合应用动力学普遍定理,是一个比较复杂的问题,难以总结出一套通用的方法,只能大致给出一些解题的基本思路和各个定理的选用方法。
首先我们来讨论各个定理的共性和个性。动力学普遍定理研究的都是物体(质点及质点系)运动的变化与受力之间的关系,但每一定理又只建立某种运动特征量和某种力的作用量之间的关系。这表明它们既有共性,又有其特殊性。例如,动量定理和动量矩定理是矢量形式,它们既反映速度大小的变化,也反映速度方向的变化,而动能定理是标量形式,它只反映速度大小的变化;动量定理和动量矩定理涉及所有的外力,却与内力无关,而动能定理则涉及所有做功的力等。这些都是其个性的反映,这正是我们解题时选择定理的基本依据。
在解题时,根据质点或质点系的受力情况、约束情况、给定的条件及要求的未知量,并结合各定理的特点,就可判断选用那一定理求解最为简捷。例如已知量和待求量是速度、加速度、外力(特别是理想约束的约束反力),而系统的内力又比较复杂时,一般可选用动量定理或质心运动定理求解。对于转动或系统仅有一个固定轴的问题,选用刚体定轴转动微分方程或动量矩定理求解较合适。对单一刚体作平面运动的问题,应选用刚体平面运动微分方程求解。若已知量和待定量是速度、加速度、作用力和路程时,特别是系统比较复杂且约束为理想约束时,选用动能定理求解比较合适。有的问题不能只用某一定理单独求解,而必须同时并用其他定理才能求解。因此,首先必须对各定理有较透彻的了解,弄清什么样的问题宜用什么定理求解,才能进一步掌握各定理的综合应用。
【例12-12】 建立例11-13中圆轮质心C的运动微分方程。
解:在例11-13中,我们应用刚体的平面运动微分方程建立了圆轮质心C的运动微分方程。现在用其他方法建立该方程(见图12-29)。
方法一:应用功率方程。
均质圆轮作平面运动,其动能为
![]()
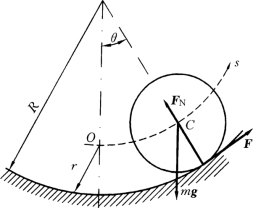
图12-29
因圆轮只滚不滑,故其约束为理想约束,在运动过程中只有重力做功,重力的功率为
![]()

方法二:用机械能守恒定律求解。
从方法一的分析已知,圆轮运动过程中只有重力做功,因此系统的机械能守恒。要求的是运动微分方程,所以应建立任意位置的机械能,并利用Ek+EP=常数,来求解。
选取质心的最低位置O为重力势能零点,则圆轮在任一位置的势能为
![]()
该位置的动能为
![]()
由机械能守恒有

此题也可用动能定理求解。
【例12-13】 半径为R、重为P的均质圆盘,可绕水平轴O转动,如图12-30所示。圆盘从图示虚线位置(φ=0)无初速释放。求当圆盘转过φ角时的速度ω、角加速度α及O 点的约束反力。
解:首先采用两种方法求圆盘转过φ角时的角速度ω 和角加速度α。
方法一:用机械能守恒定律求解。
取圆盘为研究对象,研究圆盘由φ=0转到φ角的过程。圆盘受有重力P、约束反力FRx和FRy。显然约束反力不做功,只有重力做功,故系统的机械能守恒。
取O点为重力零势能点,则在φ=0位置有
![]()
在φ角位置时有
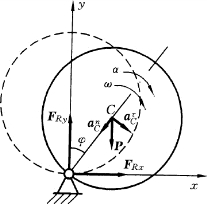
图12-30

方法二:应用刚体绕定轴转动微分方程求解。
研究对象和受力分析同前,由定轴转动微分方程有

结果同前,ω和α还可用动能定理求解。(https://www.xing528.com)
求O轴的约束反力可采用质心运动定理。取坐标Oxy,则
也可以采用质心运动定理在自然轴系上的投影计算,即

此法比直角坐标法计算简单些。

图12-31
【例12-14】 均质圆柱形滚子C重为P,半径为R,被缠绕其上的绳子拉动后可沿水平面作纯滚动,绳跨过重为G,半径为r的定滑轮(质量分布在轮缘)B,绳另一端悬挂一重为Q的重物A,如图12-31所示。绳重不计,轴承B处的摩擦力不计。试求圆柱形滚子中心C的加速度,水平段绳子的拉力及水平面对滚子的摩擦力。
解:本题是由多个物体所组成的质点系。题目既要求运动量,又要求约束反力,属综合性问题,需用多个定理求解。
首先求圆柱C质心的加速度aC。求加速度一般用动能定理的微分形式或功率方程较方便,这里我们采用功率方程求aC。
取整个系统为研究对象。由已知可知,系统的约束反力不做功,整个系统只有重力Q做功。系统的功率为
![]()
式中:vA 为重物A 在任意位置的速度。系统在任一瞬时的动能为

此过程也可由动能定理、机械能守恒定律求解。
求水平段绳的拉力与水平面的摩擦力可采用刚体平面运动微分方程求解。

F<0,说明静滑动摩擦力实际指向与图设相反。
本题还可采用其他方法求解,读者可试一试。
【例12-15】 无重刚杆AB的一端固连一重为P2 的质点B,另一端用铰链连接在置于光滑水平面上的重为P1 的滑块A的中心,如图12-32 (a)所示。AB=l,不计摩擦,设开始释放时杆AB处于水平位置,初速度为零,滑块A静止。求杆AB摆到铅垂位置时质点B和滑块A 的速度。

图12-32
解:取系统为研究对象,受力分析如图12-32所示,设在铅垂位置时滑块A的速度为vA,质点B的速度为vB,且vB=vA+vBA,方向如图12-32所示。
由受力图可知,系统的受力满足∑Fx =0,即系统Ox方向的动量守恒。因初瞬时系统静止,所以有

式中:vA 和vB 均为未知量,故不能求解,必须再应用其他定理,列出补充方程才能求解。
由受力分析可知,系统在运动过程中,只有质点B的重力P2 做功,故系统在此过程中机械能守恒,取系统的初位置为重力的零势能位置,则系统在初位置时的动能的和势能分别为
![]()
系统在铅垂位置时的动能和势能为

由机械能守恒定律
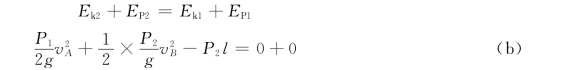
联立式(a)和式(b)解得
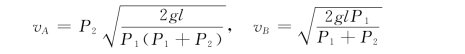
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




