机械能守恒定律及应用

质点系在某瞬时的动能和势能的代数和称为机械能。设质点系在运动过程的位置1和位置2的动能分别为Ek1和Ek2，所受的力在从位置1运动到位置2的过程中所做的功为W12，则由动能定理有

如果质点在运动过程中，只有势力做功，则由式（12-36）有此即机械能守恒定律，即质点系在运动过程中只有有势力做功，则其机械能保持不变。这样的质点系称为保守系统。根据这一定律，质点在势力场中运动时，动能和势能可以相互转化，但其和保持不变。

如果质点系还受到非保守力的作用，则称为非保守系统。非保守系统的机械能是不守恒的。

应用机械能守恒定律解题的基本步骤如下：

（1）选取某质点或质点系为研究对象，分析研究对象所受的所有做功力是否为有势力，若是，则应用机械能守恒定律。

（2）确定应用定律的始、末位置。

（3）选取零势能位置，分别计算始、末位置的动能和势能。

（4）应用机械能守恒定律求解。

【例12-10】 重P、半径为R的均质圆柱形滚子，可沿与水平面成角θ的斜面作无滑动的滚动，如图12-27所示，在滚子中心轴C上连结一刚度系数为k的弹簧。设开始时，滚子处于静止，此时弹簧无变形。试求滚子中心C沿斜面移动路程s时的速度。

解：取滚子为研究对象，研究滚子从静止到C移动路程s的过程，在此过程中只有重力和弹性力做功，故在此过程中机械能守恒。

初始时系统静止，Ek1=0，在末位置时

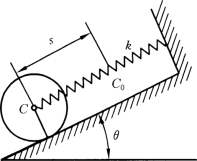
图12-27

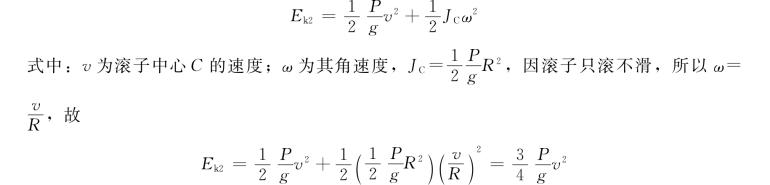
取开始时轮心的静止位置为重力和弹性力的零势能点，则轮子在初、末位置时的势能分别为

(www.xing528.com)

由机械能守恒定律有

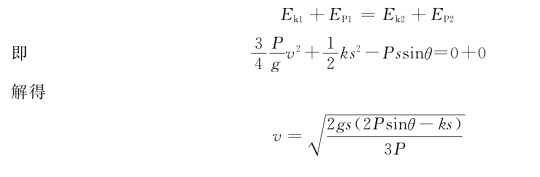
图12-28

【例12-11】 如图12-28所示，摆的质量为m，点C为质心，O端为光滑铰支，在D 处用弹簧悬挂，可在铅锤平面内摆动。设摆对水平轴O的转动惯量为JO，弹簧的刚度系数为k；摆杆在水平位置处平衡。设OD=CD=b。求摆从水平位置处以初角速度ω0 向下作微幅摆动时，摆的角速度与φ角的关系。

解：取摆为研究对象，此系统只有弹性力和重力做功，为保守系统，故可应用机械能守恒定律。

取摆在水平位置时为初位置，并以此时位置为零势能位置；取摆杆摆过微小角度φ时为末位置。则在初位置时有

式中：δ0 为水平位置时弹簧的伸长量；δ为末位置时弹簧的伸长量，δ=δ0+bφ。

因在平衡位置时满足平衡方程∑MO（F）=0，即

由机械能守恒可得

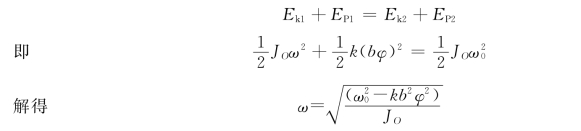
如此系统以水平位置为重力零势能点，以弹簧自然位置 （原长位置）为弹性零势能点，则

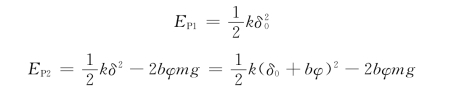
其解题结果相同，可见，对于受多种有势力作用的系统，其各有势力可选取各自的零势能位置，也可统一选取零势能位置。对于不同的零势能位置，系统的势能是不同的。另外，由本题的解题过程还可看出，对于常见的重力——弹性力系统，以其平衡位置为零势能点，往往是更方便的。