物块由弹簧原长位置沿斜面下移0.5m时力的功劳

1．重力的功

质点在地面附近运动时，所受重力P可看作是不变的，取坐标系Oxyz的z轴铅直向上，质点沿轨道由M1 运动到M2，如图12-9所示。则重力P在各坐标轴上的投影为Fx=0，Fy=0，Fz=-P，于是由式（12-6）得重力的功为

对于质点系，设有n个质点，其中任一个质点Mi所受的重力为Pi，则整个质点系所受的重力的功为

由重心坐标公式有∑Pizi1=∑PizC1，∑Pizi2=∑PizC2，令P=∑Pi是整个质点系的重量，则

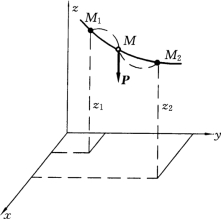
图12-9

式中：zC1和zC2为质点系在位置1和位置2时的重心的z坐标。

由式（12-7）和式（12-8）可见，重力所做的功只与质点或质点系重心的起始位置与终了位置的高度差有关，而与所经的路径无关。重心下降，重力做正功；重心上移，重力做负功。

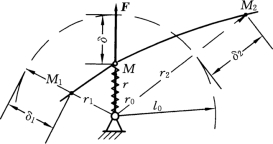
图12-10

2．弹性力的功

物体受到弹性力的作用，作用点M 的轨迹如图12-10所示。设弹簧的原长为l0，刚度系数为k，其单位为N/m。在弹性极限内，由胡克定律，弹性力的大小为

其方向总是指向自然位置。r为点M 对固定点的矢径r的长度。

若设矢径方向的单位矢量为r0，并考虑到弹性力的方向，则弹性力可表示为

当弹簧伸长时，r＞l0，力F与r0 的方向相反；当弹簧被压缩时，r＜l0，力F与r0的方向一致。

由式（12-5）可得弹性力的作用点M 由M1 运动到M2 位置时，弹性力做的功为

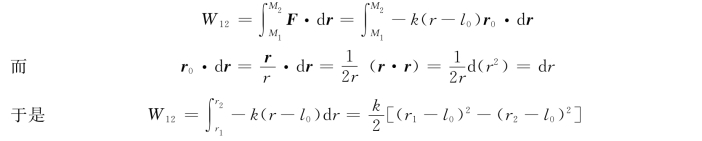
令δ1=r1-l0，δ2=r2-l0，分别为弹簧在起止位置时的变形量，则

由式（12-9）可知，弹性力的功也只与其作用点M 的起止位置有关，即只与弹簧在起止位置的变形量δ有关，而与弹性力作用点M 的运动路径无关。

3．作用于绕定轴转动刚体上的力及力偶的功

在绕z轴转动的刚体A 点作用一力F，如图12-11所示。设力F与力作用点A 处的轨迹切线之间的夹角为θ，则力F在切线方向的投影为

(www.xing528.com)

因刚体绕定轴转动时转角φ与弧长s的关系为

式中：R为力作用点到转轴的垂直距离，于是力F的元功为

因FτR=Mz，于是

力F在刚体从角φ1 和φ2 的过程中所做的功为

如果力矩是常数，则

若作用于转动刚体上的是力偶，则力偶所做的功仍可用上述公式计算，其中Mz 为力偶对转轴z的矩，即力偶矩矢在轴上的投影。

当刚体作面运动时，作用于刚体的力偶所做的功可同样计算。

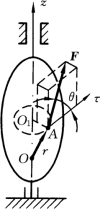
图12-11

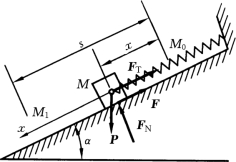
图12-12

【例12-1】 质量m=20kg的物块M 置于倾角α=30°的斜面上，并用刚度系数k=120N/m的弹簧系住，如图12-12所示。斜面的滑动摩擦因素f=0．2。试计算物块由弹簧原长位置M0 沿斜面下移s=0．5m到达M1 位置时，作用于物块M 上各力的功及合力的功。

解：取物块M 为研究对象，坐标如图12-12所示，M0 为其原点。受力分析如图12-12所示，其中P为重力，FT 为弹簧力，FN 斜面法向反力，F 为动滑动摩擦力。由∑Fy =0，得

上述四个力中法向反力FN 不做功，其余三个力作功。于是由式 （12-8）得重力P的功为

由式（12-1b）得动摩擦力的功为

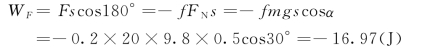
由式（12-9）得弹性力的功为

合力的功为