【摘要】：下面就不变质点系（刚体）作平动、定轴转动以及平面运动时的动量矩加以计算并讨论。设刚体以角速度ω 绕固定轴（z轴）转动，如图11-2所示，刚体内任一点的质量为mi，转动半径为ri，则对转轴子的动量矩为图11-3令∑mir2i=Jz，称为刚体对z轴的转动惯量，则得即绕定轴转动刚体对其转轴的动量矩等于刚体对转轴的转动惯量与转动角速度的乘积。由转动惯量的定义式知，其值是正的标量，所以动量矩的符号与角速度的符号相一致。
对于n个质点组成的质点系，能列出n个这样的方程并相加得
由牛顿第三定律知，作用在质点上的内力成对出现，且大小相等方向相反，即Fij=-Fji其中，（i，j=1，2，…，n且i≠j），所以内力的主矩为
上式左端
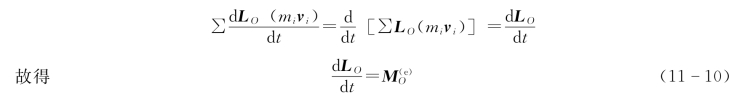(www.xing528.com)
由式（11-10）知，质点系对某固定点的动量矩对时间的导数，等于作用于质点系的外力对同一点的力矩。将此式称为质点系的动量矩定理。
将式（11-10）投影到固定坐标轴上，可得质点系对轴的动量矩定理，即
即质点系对某固定轴的动量矩对时间的导数等于作用于该质点系所有外力对同一轴之矩的代数和。
质点系动量矩定理不包含内力，说明内力不能改变其动量矩，只有外力才能改变质点系的动量矩，但内力可以改变质点系内各质点的动量矩，即起着传递作用。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
