质心运动定律与质心守恒原理

质心运动定理的表达式∑F（e）=MaC 中，如果外力主矢量∑F（e）=0，得aC=0或vC=常矢量。

1．vC=常矢量≠0

即当作用于质点系的外力主矢等于零时，则质心保持匀速直线运动状态，即动量守恒。

2．vC=常矢量=0

即当作用于质点系的外力主矢等于零时，且初瞬时质心静止，则质心的位置始终不变，称为质心位置守恒。

如果虽然外力主矢量∑F（e）≠0，但是外力主矢量在某一方向上 （比如x轴方向）投影∑F（e）x =0，则得aCx=0或vCx=常数。

（1）vCx=常数≠0，即当作用于质点系的所有外力在某轴上投影的代数和等于零，则质心的速度在该轴上的投影是常量。

（2）vCx=常数=0，即当作用于质点系的所有外力在某轴上投影的代数和等于零，且初速度投影等于零，则质心在该轴上投影的坐标保持不变，即xc=常量。称为质心在某方向的位置守恒。

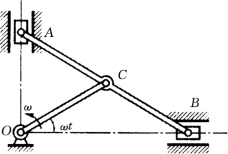
图10-3

【例10-1】 如图10-3所示，椭圆规尺AB的质量为2m1，曲柄OC的质量为m1，而滑块A和B 的质量均为m2。已知：OC=AC=CB=l；曲柄和尺的质心分别在其中点上；曲柄绕O 轴转动的角速度ω 为常数。试求该机构（质点系）的动量。

解：此质点系统由两部分组成：一部分为尺AB与滑块A、B，另一部分为曲柄OC，根据质点系的动量计算式，有

因为vC 和vC1均垂直于OC曲柄，故动量p也垂直于OC。将vC=2vC1=lω代入上式得

【例10-2】 电动机的外壳固定在水平基础上，定子质量为m1，转子质量为m2。转子的转轴通过定子的质心O1，但由于制造误差，转子的质心O2 到O1 的距离为e，如图10-4所示。已知转子匀速转动角速度为ω。求基础的反力。

解：选取整个电机为研究的质点系。这样可以不考虑使转子转动的内力；外力有定子的重力m1g，转子的重力m2g，基础的反力Fx、Fy 和反力偶M。

建立直角坐标系如图10-4所示，则质点系质心的坐标为

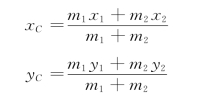
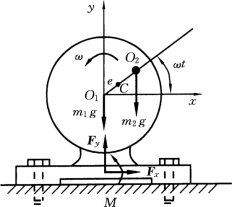
图10-4

其中x1 和y1 为定子质心O1 的坐标x1=y1=0，x2、y2 为转子质心O2 的坐标，则x2=ecosωt，y2=esinωt。所以

根据质心运动定理在直角坐标轴上的投影得

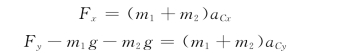
式 （a）求导并代入上式得

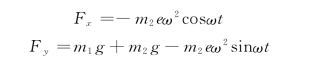
可以看出，电动机的支座反力是时间的正弦和余弦函数，即大小和方向是变化的。这种变化的作用力常成为振动的激励源，影响很大。因此，转子的平衡 （消除偏心距e）的问题，是工程中一个很重要的实际问题。

用质心运动定理只能求出Fx、Fy，而对约束反力偶却无能为力，这可用动量矩定理解决，读者在学完下一章之后可自己求解。

【例10-3】 如图10-5所示，设例10-2中的电机没用螺栓固定，各处摩擦不计，求电动机外壳的运动。设定子由静止开始运动。

解：取电机定子，转子为研究的质点系。电机受到的作用力有定子和转子的重力，以及地面的法向反力。

因为∑Fx（e ）0，且电机初始为静止，因此系统质心的坐标xc保持不变。

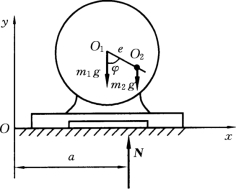
图10-5

建立坐标系如图10-5所示。转子在静止时，设xC1=a，当转子转过角度φ=ωt时，定子必定向左移动，设移动距离为s，此时

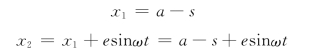
则质心坐标为

(www.xing528.com)

因为在水平方向质心守恒，所以有xC1=xC2，解得

综合以上各例可知，应用质心运动定理解题的步骤如下：

（1）分析质点系所受的全部外力，包括主动力和约束反力。

（2）根据外力主矢是否等于零，确定质心运动是否守恒。

（3）如果外力主矢等于零，且质心初速度为零，则质心坐标保持不变，计算任一瞬时质心坐标和初瞬时质心坐标，令其相等，即可得到所要求的质点位移。

（4）如果外力主矢不等于零，则计算任一瞬时质心坐标，求质心的加速度，然后应用质心运动定理求未知力。若在质点系上作用的未知力，在某一方向有两个以上，则质心运动定理只能求出它们在这个方向投影的代数和。

（5）在外力已知时，欲求质心的运动规律，与求解质点的运动规律相同。

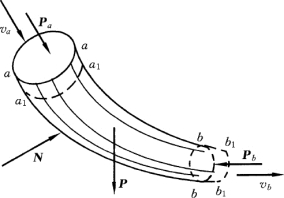
图10-6

【例10-4】 如图10-6所示，表示水流经变截面弯管的示意图。设流体是不可压缩的，流动是稳定的 （即管内任一截面上的流速不随时间而变化）。求流体对管壁的附加动压力。

解：取管中任意两截面aa和bb间的流体为研究的质点系。质点系受的外力有重力P、两截面受相邻流体的压力Pa 和Pb及管壁对流体反力的合力N。

假如经过无限小的时间间隔dt，这一部分流体流到两截面a1a1 和b1b1 之间。设Q为流体的流量（即每秒钟流过任一截面的流体体积），ρ为密度，则质点系在dt时间间隔内流过截面的质量为

在时间间隔dt内质点系的动量变化为

因为管内流动是稳定的，有pa1b =p′a1b ，因此

当dt取极小时，可认为截面aa与a1a1 之间各质点的速度相同，截面bb与b1b1 之间各质点的速度也相同，于是得

应用质点系动量定理可得

消去dt得

因管壁对流体的反力N 包含两部分：N静为不考虑流体动量改变时管壁的静反力，N动为由于流体的动量变化而产生的附加动压力，则

附加动压力由下式确定

设截面aa和bb的面积分别为Aa 和Ab，由不可压缩流体的连续性定律知

因此，只要知道流速和曲管的尺寸，即可求得附加动反力。流体对管壁的附加动压力与N动大小相等，方向相反。在应用前面的结论时应取投影式。

如图10-7所示，为一水平的等截面直角形弯管，当流体被迫改变流动方向时，对管壁施加的附加动压力的大小等于管壁对流体作用的附加动反力，即

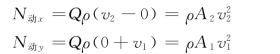
可见，当流速很高或管子的横截面积很大时，附加动压力很大，因此在管子的弯头处必须安装支座。

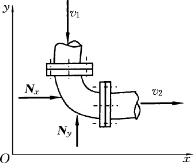
图10-7