动量设定及应用于质点系

例如，射出枪膛的子弹，质量虽然很小，但其速度很大，也能穿入或穿透障碍物。又如质量很大的轮船，虽然速度很小，当其靠岸时也需小心行事，如果稍一疏忽，足以将船撞坏等等。实践证明，物体的机械运动量的强弱，不仅取决于速度，而且还取决于质量。因此，引入与物体的质量和速度相关的一个物理量来描述物体机械运动的强弱程度，即：动量。

（一） 质点的动量

质点的质量m与它的速度v的乘积mv，称为质点的动量，用p来表示，即

动量是一瞬时矢量，方向与速度一致。在国际单位制中，动量的单位是kg·m/s或N·s。

（二） 质点系的动量

设有一n个质点组成的质点系，某瞬时质量为mi的第i个质点的速度为vi，则由单个质点的动量定义知，第i个质点的动量为

则质点系的动量为

❖质心（质点系的质量中心）

质点系的运动不仅与所受的力有关，而且与质点系质量的分布情况有关，而质量分布的特征之一可以用质量中心（简称质心）来描述。(www.xing528.com)

设有一n个质点组成的质点系，质点系中第i个质点的质量为mi，它的位置可由以O为参考点的位置矢径r表示，如图10-1所示，则质心C的位置由下式决定

式中：M=∑mi，是质点系的总质量。

将式（10-3）变形并对时间求导得

图10-1

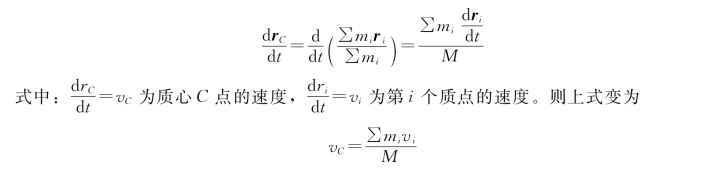
所以，质点系的动量为

式（10-4）表明质点系的质量与质心速度的乘积等于质点系的动量，它给出了质点系动量的简捷求法。由公式知，不论质点系内各质点的速度如何不同，只要知道质心的速度，就可以求出整个质点系的动量。