质点动力学的两类基本问题-《理论力学》成果

由上面质点运动微分方程可求解质点动力学的两类问题：

（1）已知质点的运动，求作用于质点上的力，称为质点动力学第一类问题。在求解过程中需对运动方程求导即可。

（2）已知作用于质点上的力，求质点的运动，称为质点动力学第二类问题。在求解过程中需解微分方程，即求积分的过程。

在此两类问题基础上，有时也存在两类问题的联合求解。

【例9-1】 质点的质量m=0．1kg，按x=t4-12t3+60t2 的规律作直线运动，x以“m”计，时间t以 “s”计，试求该质点所受的力，并求其极值。

解：当质点作直线运动时其运动微分方程为

则作用在该质点上的力为

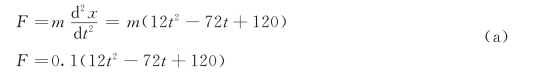
对式（a）求导

得时间为

将式（b）代入式（a）得作用在该质点上的最小力为

上面的例子为质点动力学第一类问题，在这类问题的求解时应做到以下几点：

（1）根据题意选择适当的质点运动微分方程形式。

（2）正确地对质点进行力和运动分析。

（3）利用质点运动微分方程求质点所受的力。

【例9-2】 质点的质量m，在力F=F0-kt的作用下，沿x轴作直线运动，F0、k为常数，当运动开始时即t=0，x=x0，v=v0，试求质点的运动规律。

解：根据题意，采用直角坐标形式的质点运动微分方程，即

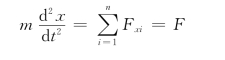
则有

采用分离变量法积分，得

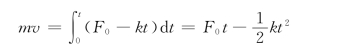
再积分，得质点的运动方程为

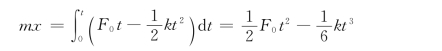
即解：根据题意，采用自然法求解。质点的切向运动微分方程为

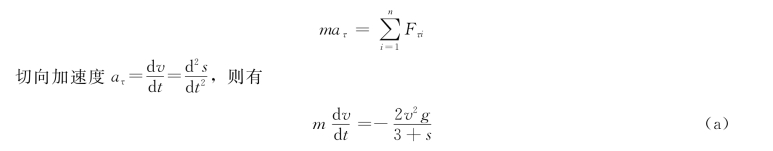
将切向加速度进行如下的变换

式 （b）代入式（a）有

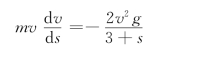
应用分离变量法

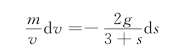
积分

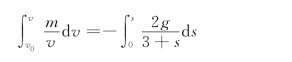
得

则得质点的速度为(www.xing528.com)

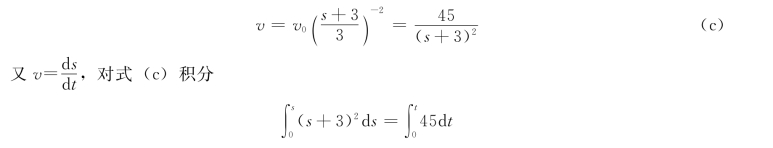
质点的运动规律为

例9-2和例9-3为质点动力学第二类问题。在求解时应根据题意将运动量进行变换，才能求解。求解的步骤与质点动力学第一类问题基本相同，解这类问题是解微分方程的过程，一般采用分离变量法求解。

【例9-4】 一圆锥摆，如图9-3所示，质量为m=0．1kg的小球系于长为l=0．3m的绳上，绳的另一端系在固定点O上，并与铅垂线成θ=60°角，若小球在水平面内做匀速圆周运动，试求小球的速度和绳子的拉力。

解：以小球为质点，小球的受重力mg及绳子的拉力F及运动如图9-3所示，采用自然法求解。其运动微分方程为

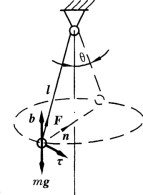
图9-3

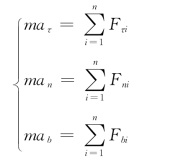
其切向运动微分方程为

法向运动微分方程为

副法向运动微分方程为

由于副法向加速度ab=0，则由式（b）绳子得拉力为

因圆的半径ρ=lsinθ，将上面绳子的拉力代入式（a）得小球的速度为

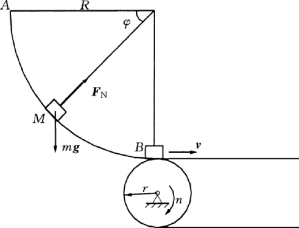
图9-4

【例9-5】 如图9-4所示，物块M 自点A沿光滑的圆弧轨道无初速地滑下，落到传送带上B，已知圆弧的半径为R，物块M 的质量为m，试求物块M 在圆弧轨道上点B 的法向约束力，若物块M 与传送带间无相对滑动，试确定半径为r的传送轮的转速。

解：根据题意，物块M 沿光滑圆弧轨道的运动为轨迹曲线为已知的运动，故采用自然法求解。如图9-4所示，质点的切向运动微分方程为

式中，φ为物块M 对应的半径与水平线的夹角。

切向加速度为

式 （b）代入式（a）并进行分离变量，积分得

同时注意ds=Rdφ，则式（c）变为

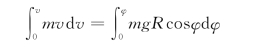
解得质点的速度为

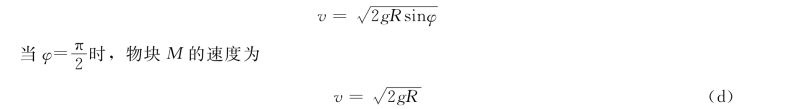
物块M 在圆弧轨道上点B 的法向运动微分方程为

将式（d）代入式（e）得物块M 在上点B 的法向约束力为

传送轮的转速为

例9-4和例9-5为两类问题的联合求解。