理论力学第五节：运动学综合问题分析

工程中的机构都是由数个物体组成的，各物体间通过连接点而传递运动。为分析机构的运动，首先要分清各物体做什么运动，要计算有关连接点的速度和加速度。

为分析某点的运动，如能找出其位置与时间的函数关系，则可直接建立运动方程，用解析法求其运动全过程的速度和加速度。当难以建立点的运动方程或只对机构某些瞬时位置的运动参数感兴趣时，可根据刚体各种不同运动形式，确立此刚体的运动与其上一点运动关系，并常用合成运动或平面运动的理论来分析相关的两个点在某瞬时的速度和加速度关系。

平面运动理论用来分析同一平面运动刚体上两个不同点间的速度和加速度联系。当两个刚体相接触而有相对滑动时，则需用合成运动的理论分析这两个不同刚体上相重合一点的速度和加速度联系。两物体间有相对运动，虽不接触，其重合点的运动也符合合成运动的关系。复杂机构中，可能同时有平面运动和点的合成运动问题，应注意分别分析，综合运用有关理论。下面通过几个例题说明这些方法的综合应用。

【例8-9】 图8-24所示平面机构，滑块B可沿杆OA 滑动。杆BE与BD 分别与滑块B 铰接，BD 可沿水平导轨运动。滑块E 以匀速v沿铅直导轨向上运动，杆BE长为图示瞬时杆OA 铅直，且与杆BE 夹角为45°，求该瞬时杆OA的角速度和角加速度。

解：BE杆作平面运动，可先求出点B的速度和加速度。点B连同滑块在OA 杆上滑动，并带动杆OA 转动，可按合成运动方法求解杆OA的角速度和角加速度。

BE杆作平面运动，在图8-24中，由vE 及vB 方向可知此瞬时点O为BE 的速度瞬心，因此

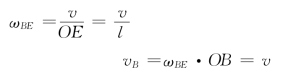
图8-24

以E为基点，点B的加速度为

式中各矢量方向如图8-24所示。由于点E作匀速直线运动，故aE=0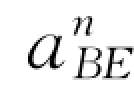，的大小为

将式（a）投影到沿BE方向的轴上，得

因此

上面由刚体平面运动方法求得了滑块B的速度和加速度。由于滑块B可以沿杆OA滑动，因此应利用点的合成运动方法求杆OA的角速度和角加速度。取滑块B为动点，动系固结在杆OA上，点的速度合成定理为

其中va=vB；牵连速度为OA杆上与滑块B 重合的那一点的速度，其方向垂直于OA，因此与va同向；相对速度vr沿OA杆，即垂直于va。显然有

即

于是得杆OA的角速度

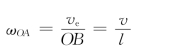
其转向如图8-24所示。

滑块B的绝对加速度aa=aB，其牵连加速度有法向及切向二项，其法向部分为

由于滑块B的相对运动为沿OA 杆的直线运动，因此其相对加速度ar也沿OA方向。这样有

因为该瞬时vr=0，故aC=0。在此矢量式中，各矢量方向已知，如图8-25所示；未知量为ar及aτe的大小，共两个。将式（b）投影到与ar垂直的BD线上，得

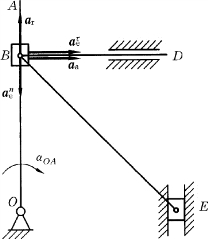
图8-25

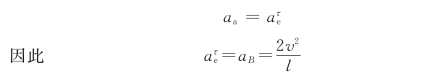
杆OA的角加速度为

(www.xing528.com)

角加速度方向如图8-25所示。

上面的求解方法是依次应用刚体平面运动及点的合成运动方法求解，这是机构运动分析中较常用的方法之一。

【例8-10】 图8-26 （a）所示平面机构，AB长为l，滑块A可沿摇杆OC 的长槽滑动。摇杆OC以匀角速度ω绕O 转动，滑块B以匀速v=ωl沿水平导轨滑动。图示瞬时OC铅直，AB与水平线OB 夹角为30°。求此瞬时AB杆的角速度及角加速度。

图8-26

解：杆AB作平面运动，点A又在摇杆OC内有相对运动，这是一种应用平面运动和合成运动理论联合求解的问题，而且是一种含两个运动输入量ω和v的较复杂的机构运动问题。

杆AB作平面运动，以B为基点，有

点A在杆OC内滑动，因此，需用点的合成运动法，取点A为动点，动系固结在OC上，有

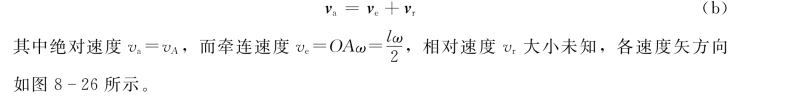
由式（a）和式（b），得

其中vB=v为已知，ve已求得，且vAB和vr方向已知，仅有vAB及vr两个量的大小未知，故可解。

将此矢量方程沿vB 方向投影，得

因此

AB杆的角速度方向如图，大小为

将式（c）沿vr方向投影，得

故

以B为基点，则点A的加速度为

由于vB 为常量，所以aB=0，而

仍以点A为动点，动系固结于OC上，则有

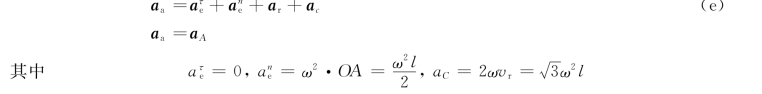
由式（d）和式（e）得

由此得AB杆的角加速度为

方向如图8-26 （b）所示。