平面图形内各点的速度和分布，理论力学

根据上述定理，每一瞬时在图形内都存在速度等于零的一点C，即vC=0。选取C做为基点，图8-14 （a）中A，B，D等各点的速度为

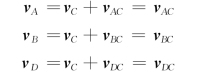
由此得到结论：平面图形内任一点的速度等于该点随图形绕瞬时速度中心转动的速度。

由于平面图形绕任意点转动的角速度都相等，因此图形绕速度瞬心C转动的角速度等于图形绕任一基点转动的角速度，以ω表示这个角速度，于是

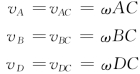
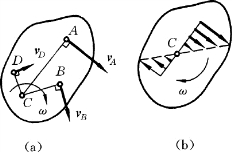
图8-14

由此可见，图形内各点的速度大小与该点到速度瞬心的距离成正比。速度的方向垂直于该点到速度瞬心的连线，指向图形转动的一方，如图8-14 （a）所示。

平面图形上各点速度在某瞬时的分布情况与图形绕固定轴转动时各点的速度分布情况相类似 [见图8-14 （b）]。于是，平面图形的运动可看作绕速度瞬心的瞬时转动。

注意：刚体作平面运动时，在每一瞬时，图形内必有一点成为速度瞬心，但是在不同瞬时，速度瞬心在图形内的位置是不同的。

综上所述可知，如果已知平面图形在某一瞬时的速度瞬心位置和角速度，则在该瞬时，图形内任一点的速度可以完全确定。在解题时，根据机构的几何条件，确定速度瞬心位置的方法有下列几种：

（1）平面图形沿一固定表面做无滑动的滚动，如图8-15所示。图形与固定表面的接触点C就是图形的速度瞬心，因为在这一瞬时，点C相对于固定面的速度为零，所以它的绝对速度等于零。车轮滚动的过程中，轮缘上的各点相继与地面接触而成为车轮在不同时刻的速度瞬心。

（2）已知图形内任意两点A和B的速度方向，如图8-16所示，速度瞬心C的位置必在每一点速度的垂线上。因此在图8-16中，通过点A，做垂直于vA 方向的直线Aa；再通过点B，做垂直于vB 方向的垂线Bb，则二条直线的交点C就是平面图形的速度瞬心。

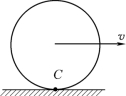
图8-15

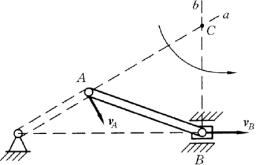
图8-16

（3）已知平面图形上两点A和B 的速度相互平行，并且速度的方向垂直于两点的连线AB，如图8-17所示，则速度瞬心必定在连线AB与速度矢vA 和vB 端点连线的交点C上 [见图8-14 （b）]。因此，与确定图8-17所示齿轮的速度瞬心C的位置，不仅需要知道vA 和vB 的方向，而且还需要知道它们的大小。

当vA 和vB 同向时，图形的速度瞬心在AB的延长线上 [见图8-17 （a）]；当vA 和vB 反向时，图形的速度瞬心在A、B二点之间[见图8-17 （b）]。

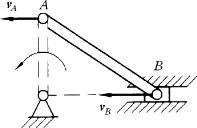
（4）某一瞬时，图形上A、B两点的速度相等，即vA=vB 时，如图8-18所示，图形的速度瞬心在无限远处。在该瞬时，图形上各点的速度分布如同图形作平动的情形一样，故称瞬时平动。必须注意，此瞬时各点速度虽然相同，但加速度不同。

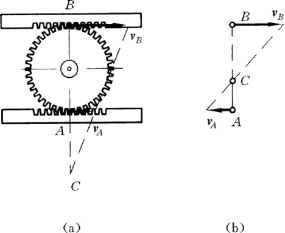
图8-17

(www.xing528.com)

图8-18

【例8-5】 车厢的轮子沿直线轨道滚动而无滑动，如图8-19所示。已知车轮中心O的速度为vO。如半径R和r都是已知的，求轮上A1、A2、A3、A4 各点的速度，其中A2、O、A4 三点在同一水平线上，A1、O、A3 三点在同一铅垂线上。

解：因为车轮只滚动无滑动，故车轮与轨道的接触点C就是车轮的速度瞬心。令ω为车轮转动的角速度，因vO=rω，从而求得车轮的角速度，转向如图，大小为

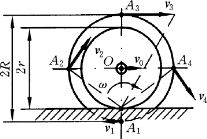
图8-19

图8-19中各点速度分别计算如下

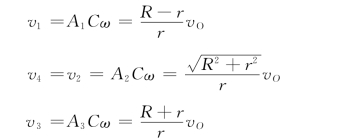
这些速度方向分别垂直于A1C、A2C、A3C和A4C，指向如图8-19所示。

【例8-6】 用瞬心法解例8-1。

解：分别作A和B 两点速度的垂线，两条直线的交点C就是图形AB 的速度瞬心，如图8-20所示。

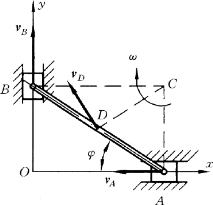
图8-20

点B的速度为

以上结果与例8-1求得的完全一样。

用瞬心法也可以求图形内任一点的速度。例如中点D的速度为

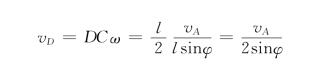
它的方向垂直于DC，且指向图形转动的一方。

由以上各例可以看出，用瞬心法的解题步骤为：第一步要分析题中各物体的运动，哪些物体做转动，哪些物体做平面运动；第二步要研究平面运动的物体上哪一点的速度大小和方向是已知的，哪一点的速度的某一要素（一般是速度方向）是已知的；第三步要根据已知条件，求出图形的速度瞬心的位置和平面图形转动的角速度，最后求出各点的速度。

如果需要研究由几个图形组成的平面机构，可依次对每一图形按上述步骤进行。应注意，每一个平面图形有它自己的速度瞬心和角速度，因此每求出一个瞬心和角速度，应明确标出它是哪一个图形的瞬心和角速度，绝不可混淆。