平面图形上点速度分析：基点法应用

设平面图形S某瞬时的角速度为ω，图形上A点的速度为vA，现在来求图形上任一点B的速度，如图8-8所示。

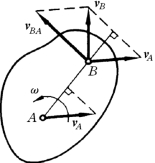
图8-8

取A点作为基点，假想在A点上固定一个平动参考系，则平面图形的运动可以分解成随A点的平动和相对于平动参考系的转动。按照点的合成运动的概念，把B点的速度vB 作为绝对速度，在上述平动参考系下，其牵连速度就是图形随基点平动的速度vA，而相对速度则是B点相对于基点A 的转动速度，记为vBA。于是根据速度合成定理

可将B的速度写成

由此得出结论：平面图形内任一点的速度等于基点的速度与该点随图形绕基点转动速度的矢量和。

式（8-2）揭示了平面图形上同一瞬时任意二点之间的速度关系。用这种方法求解平面图形上任一点的速度时，需要选择一个速度已知的点作为基点，因而这种方法称为基点法。

式 （8-2）中vBA表示B 点相对于基点A 转动的速度。vBA的方向垂直于AB 连线，其大小为vBA=ωAB。这样，已知基点A的速度和平面图形的角速度，平面图形上任意点的速度都可以求出。

由于vBA始终垂直于AB 连线，因此将式（8-2）向A，B两点连线方向投影，则有

即：平面图形上任意两点的速度在这两点连线上的投影相等。这个结论称为速度投影定理。

这个定理也可以由下面的理由来说明：因为A和B 是刚体上两点，它们之间的距离应保持不变，所以两点的速度在AB方向上的分量必须相同，否则，线段AB不是伸长，便要缩短。因此，这一定理不仅适用于刚体平面运动，也适用于刚体作其他任意的运动。

如果已知图形内一点A的速度vA 的大小和方向，又知道另一点B的速度vB 的方向，应用速度投影定理，就可以求出vB 的大小和指向。

【例8-1】 椭圆规尺的A端以速度vA 沿x轴的负向运动，如图8-9所示，AB=l，试求B端的速度及尺AB 的角速度。

解：尺AB作平面运动，因而可用公式

在本题中vA 的大小和方向以及vB 的方向都是已知的，共计有三个要素是已知的，再加上vBA的方向垂直于AB 这一要素，可以作出速度平行四边形如图8-9所示。作图时，应注意使vB 位于平行四边形的对角线上。由图中的几何关系得

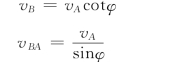
另外vBA=ωAB，此处ω是AB 的角速度，由此得

【例8-2】 图8-10平面机构中，AB=BD=DE=l=300mm。在图示位置时，BD//AE，杆AB的角速度为ω=5rad/s。试求此瞬时杆DE的角速度和杆BD 中点C 的速度。

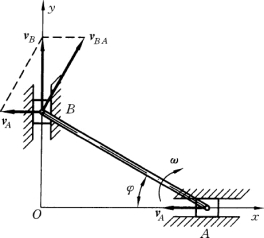
图8-9

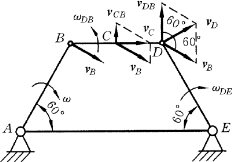
图8-10

解：杆DE绕点E 转动，为求其角速度可先求点D的速度。杆BD 作平面运动，而点B也是转动刚体AB 上的一点，其速度为

方向如图8-10所示。

对平面运动的杆BD，以点B为基点，按式（8-2）得

(www.xing528.com)

其中vB 的大小和方向已知，点D绕B 的转动速度vDB的方向与BD 垂直，点D的速度vD与DE 垂直。由于式（a）中四个要素是已知的，可以做出其速度平行四边形如图所示，其中vD 位于平行四边形的对角线。由此瞬时的几何关系得知

于是解出此瞬时杆DE的角速度为

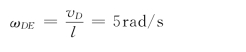
方向如图。

vDB为点D 绕B 的转动速度，应有

因此

方向如图。在求得杆BD角速度的基础上，以点B或D 为基点，求出杆BD上任一点的速度。如仍以B点为基点，杆BD中点C的速度为

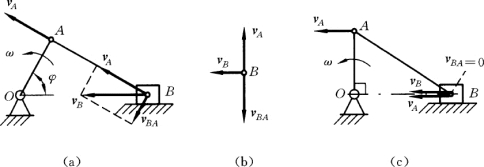
图8-11

解：连杆AB作平面运动，以点A为基点，点B的速度为

其中vA 的大小为vA=rω，方向与OA垂直；vB 沿OB 方向；vBA与AB 垂直。式中的四个要素是已知的，可以作出其速度平行四边形。

当φ=0°时，vA 与vBA均垂直于OB，也垂直于vB，按速度平行四边形合成法则，应有vB=0，如图8-11 （b）所示。

当φ=90°时，vA 与vB 方向一致，而vBA又垂直于AB，其速度平行四边形为一直线段，如图8-11 （c）所示，显然有

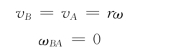
此时杆AB的角速度为零，A、B两点的速度大小与方向都相同，连杆AB具有平动刚体的特征。但杆AB只有在此瞬时有vB=vA，其他时刻则不然，因此称此时的连杆作瞬时平动。

【例8-4】 如图8-12所示平面机构中，曲柄OA=100mm，以角速度ω=2rad/s转动。连杆AB带动摇杆CD，并拖动轮E沿水平面滚动，已知CD=3CB，图示位置时A，B，E三点恰好在一条水平线上，且CD⊥ED。试求此瞬时点E 的速度。

解：vA=ωOA=0．2m/s

由速度投影定理，杆AB上点A、B的速度在AB 线上的投影相等，得

摇杆CD绕点C转动，有

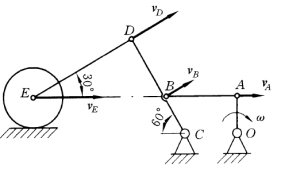
图8-12

轮E沿水平面滚动，轮心E的速度方向水平，由速度投影定理，得