理论力学：刚体平面运动概述

工程中很多构件的运动，例如行星齿轮A的运动（见图8-1）；曲柄连杆机构中连杆AB的运动（见图8-2）以及沿直线轨道滚动的轮子的运动等，这些刚体的运动即不是平动，又不是绕定轴的转动，但有一共同特点，即在运动中，刚体上的任意一点与某一固定平面始终保持相等的距离，这种运动称为平面运动。平面运动刚体上的各点都在平行于某一固定平面的平面内运动。

图8-3 （a）为一连杆的简图，用一个平行于固定平面的平面截割连杆，得截面S，它是一个平面图形，如图8-3 （b）所示。当连杆运动时，图形内任意点始终在自身平面内运动。若通过图形内任一点作垂直于图形的直线，则当刚体作平面运动时，该直线作平动，因此平面图形上的点与直线上各点的运动完全相同。由此可知，平面图形上各点的运动可以代表刚体上所有点的运动。因此，刚体的平面运动可简化为平面图形在它自身平面内的运动。

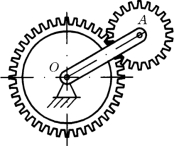
图8-1

图8-2

图8-3

平面图形在其平面上的位置完全可由图形内任意线段O′M 的位置来确定 （图8-4），而确定此线段在平面内的位置，只需确定线段上任一点O′的位置和线段O′M 与固定坐标轴Ox间的夹角φ即可。

点O′的坐标和φ角都是时间的函数，即

式 （8-1）就是平面图形的运动方程。

由式（8-1）可见，平面图形的运动方程可由两部分组成：一部分是平面图形随点O′的平动，另一部分是绕点O′的转动。

平面运动的这种分解也可以按上一章合成运动的观点加以解释。以沿直线轨道滚动的车轮为例，如图8-5 （a）所示，取车厢为动参考系，以轮心点O′为原点取动参考系O′x′y′，则车厢的平动是牵连运动，车轮绕平动参考系原点O′的转动是相对运动，两者的合成就是车轮的平面运动 （绝对运动）。车轮的平面运动可分解为平动和转动二种简单的运动。(www.xing528.com)

图8-4

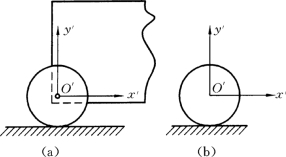
图8-5

仿照车轮，对于任意的平面运动，可在平面图形上任取一点O′，称为基点，并假想在基点处放置一个平动参考系O′x′y′，则平面运动就可以分解为随基点O′的平动和相对于基点O′的转动，如图8-6所示。

如图8-7所示的曲柄连杆机构中，曲柄OA为定轴转动，滑块B为直线平动，而连杆AB则作平面运动。如以B为基点，即在滑块B上建立一个平动参考系，以Bx′y′表示，则杆AB的平面运动可分解为随同基点B 的直线平动和在动系Bx′y′内绕基点B 的转动。同样，以A为基点，在点A安上一个平动参考系Ax″y″，杆AB的平面运动又可分解为随同基点A 的平动和绕基点A 的转动。

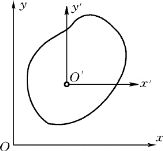
图8-6

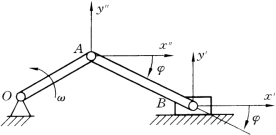
图8-7

必须指出，上述分解中，总是在选定的基点处固结一个平动的参考系，所谓绕基点的转动，是相对于这个平动参考系的转动。研究平面运动时，可以选择不同的点作为基点。一般平面图形上各点的运动是不相同的，例如，图8-7所示的连杆上的点B做直线运动，点A做圆周运动。因此，在平面图形上选取不同的基点，其动参考系的平动是不同的，其速度、加速度也不相同。如图8

7所示，还可以看出：如果运动起始时OA和AB 都位于水平位置，运动中的任一时刻，AB连线绕点A 或绕点B 的转角，相对于各自的平动参考系Ax′y′或Bx′y′都是一样的，都等于相对于固定参考系的转角φ。由于任一时刻的转角相同，其角速度、角加速度也必然相同。于是可得结论：平面运动可取任意基点而分解为平动和转动，其中平动的速度和加速度与基点的选择有关，而平面图形绕基点转动的角速度和角加速度与基点的选择无关。这里所谓的角速度和角加速度是相对于各基点处的平动参考系而言。平面图形相对于各平动参考系（包括固定参考系），其转动运动都是一样的，角速度、角加速度都是共同的，无须标明绕哪一点转动或选哪一点为基点。