牵连运动平动加速度合成定理─《理论力学》

在图7-11中，设Oxyz为定系，O′x′y′z′为动系且作平动，M 为动点。动点M 的相对速度为

动点M 的相对加速度为

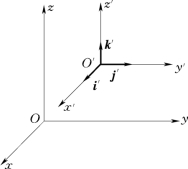
图7-11

式中：i′、j′、k′为动系坐标x′、y′、z′的单位矢量，由于动系作平动，故i′、j′、k′为常矢量，对时间的导数均为零，ve=vO′。将速度合成定理式 （7-11）对时间求导得

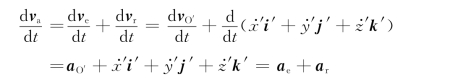
动点M 的绝对加速度为

牵连运动为平动时点的加速度合成定理：在任一瞬时，动点的绝对加速度等于在同一瞬时动点相对加速度和牵连加速度的矢量和。它与速度合成定理一样满足平行四边形合成法则，即绝对加速度位于相对加速度和牵连加速度所构成平行四边形对角线位置。在求解时也要画加速度平行四边形来确定三种加速度之间的关系。

【例7-7】 如图7-12 （a）所示，曲柄OA以匀角速度ω绕定轴O 转动，丁字形杆BC沿水平方向往复平动，滑块A在铅直槽DE 内运动，OA=r，曲柄OA与水平线夹角为φ=ωt，试求图示瞬时，杆BC的速度及加速度。

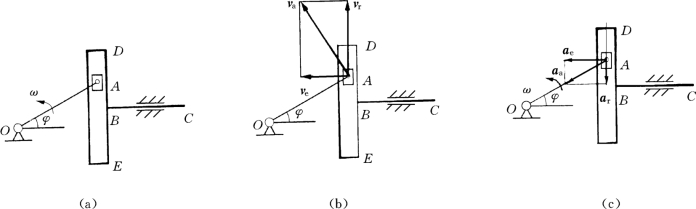
图7-12

解：滑块A为动点，丁字形杆BC为动系，地面为定系。动点A的绝对运动是以O为圆心的圆周运动，相对运动为滑块A在铅直槽DE 内的直线运动；牵连速度为T字形杆BC沿水平方向的往复平移。

（1）求杆BC的速度。作速度的平行四边形，如图7-12 （b）所示。动点A的绝对速度为

杆BC的速度为

（2）求杆BC的加速度。作加速度的平行四边形，如图7-12 （c）所示。动点A的绝对加速度为

杆BC的加速度为

【例7-8】 如图7-13 （a）所示的平面机构中，直杆O1A、O2B平行且等长，分别绕O1、O2 轴转动，直杆的A、B连接半圆形平板，动点M 沿半圆形平板ABD 边缘运动，起点为点B。已知O1A=O2B=18cm，AB=O1O2=2R，R=18cm，试求当t=时，动点M 的绝对速度和绝对加速度。

图7-13

解：根据题意，选半圆形平板ABD为动系，地面为定系。由于直杆O1A、O2B平行且等长，则动系ABD作平移，动点M 的牵连速度为

动点M 牵连速度的方向垂直于直杆O1A，沿角速度ω的转动方向。(www.xing528.com)

由于动系作曲线运动，动点M 的牵连加速度分为切向和法向加速度，即

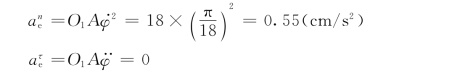
动点M 的相对速度为

同理，动点M 的相对加速度也分为切向和法向加速度，即

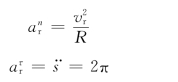
当t=3s时，动点M 的相对轨迹为

而

则当t=3s时，动点M 恰巧运动到半圆形平板ABD 最高点，动点M 相对速度的方向为水平向左，即

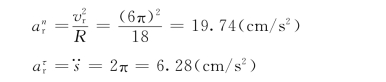
此时直杆O1A与水平线的夹角为

（1）动点M 的绝对速度。如图7-13 （b）所示，由速度合成定理的矢量形式

向直角坐标轴x、y上投影，得动点M 的绝对速度在坐标轴上的投影为

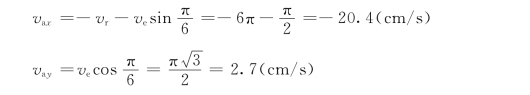
从而得动点M 的绝对速度为

（2）动点M 的绝对加速度。如图7-13 （c）所示，由牵连运动为平移时点的加速度合成定理的矢量形式

向直角坐标轴x、y上投影，得动点M 的绝对加速度在坐标轴上的投影为

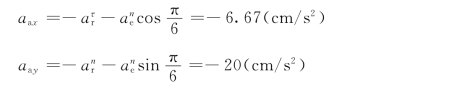
从而得动点M 的绝对加速度为