理论力学：点的合成运动概念

在工程和实际生活中物体相对于不同参考系运动的例子很多，例如沿直线滚动的车轮，在地面上观察轮边缘上点M 的运动轨迹是旋轮线，但车厢上观察是一个圆，如图7 1所示，又如在雨天观察雨滴的运动，如果在地面上观察 （不计自然风的干扰）雨滴铅锤下落，而行驶的汽车上，雨滴在车窗上留下倾斜的痕迹，如图7-2所示。

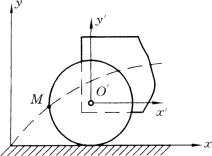
图7-1

图7-2

从上面的两个例子看出物体相对于不同参考系的运动是不同的，它们之间存在运动的合成和分解的关系。一般情况下，将研究的物体看成是动点，动点相对于两个坐标系运动，其中建立在不动物体上的坐标系称为定参考坐标系 （简称定系），如建立在地面上的坐标系，另一个坐标系相对定参考坐标系是运动的，称为动参考坐标系 （简称动系）。动点相对于定系运动可以看成是动点相对于动系的运动和动系相对定系的运动的合成。上面的例子中，定系建立在地面上，动点M 的运动轨迹是旋轮线，动系建立在车厢上，点M相对于动系的运动轨迹是一个圆，而车厢是作平移的运动。即动点M 的旋轮线可以看成圆的运动和车厢平移运动的合成。

研究点的合成运动必须要选定两个参考坐标系，清楚以下三种运动：

（1）动点相对于定参考坐标系运动，称为动点的绝对运动。所对应的轨迹、速度和加速度分别称为绝对运动轨迹、绝对速度va、绝对加速度aa。

（2）动点相对于动参考坐标系运动，称为动点的相对运动。所对应的轨迹、速度和加速度分别称为相对运动轨迹、相对速度vr、相对加速度ar。

（3）动系相对于定系的运动，称为动点的牵连运动。动系上与动点重合的点称为动点的牵连点，牵连点所对应的轨迹、速度和加速度分别称为牵连运动轨迹、牵连速度ve、牵连加速度ae。

结合所建立的两个参考坐标系和三种运动，请初学者自己分析上面的例子。

图7-3

一般来讲，绝对运动看成是运动的合成，相对运动和牵连运动看成是运动的分解，合成与分解是研究点的合成运动的两个方面，切不可孤立看待，必须用联系的观点去学习。

动点的绝对运动、相对运动和牵连运动之间的关系可以通过动点在定参考坐标系和动参考坐标系中的坐标变换得到。以平面运动为例，设Oxy为定系，O′x′y′为动系，M 为动点，如图7-3所示，

M 点绝对运动方程为

M 点相对运动方程为

牵连运动是动系O′x′y′相对于定系Oxy的运动，其运动方程为

由图7-3的坐标变换

【例7-1】 半径为r的轮子沿直线轨道无滑动地滚动，如图7-4所示，已知轮心C的速度为vC，试求轮缘上的点M绝对运动方程和相对轮心C的运动方程和牵连运动方程。

解：沿轮子滚动的方向建立定系Oxy，初始时设轮缘上的点M 位于y轴上MO 处。在图示瞬时，点M 和轮心C的连线与CH 所的夹角为(www.xing528.com)

在轮心C建立动系Cx′y′，点M 的相对运动方程为

点M 相对运动轨迹方程为

图7-4

由式（b）知点M 的相对运动轨迹为圆。

牵连运动为动系Cx′y′相对于定系Oxy的运动，其牵连运动方程为

其中，由于动系作平动，因此动系坐标轴x′与定系坐标轴x的夹角φ=0。

由式（7-4）得点M 绝对运动方程为

点M 的绝对运动轨迹为式（d）表示的旋轮线。

【例7-2】 用车刀切削工件直径的端面时，车刀沿水平轴z作往复的运动，如图7 5所示。设定系为Oxyz，刀尖在Oxy面上的运动方程为x=rsinωt，工件以匀角速度ω绕z轴转动，动系建立在工件上为Ox′y′z′，试求刀尖在工件上画出的痕迹。

图7-5

解：由题意知，刀尖为动点，刀尖在工件上画出的痕迹为动点相对运动轨迹。由图7-5 （b）得动点相对运动方程为

削去时间t，得动点相对运动轨迹方程为

则刀尖在工件上画出的痕迹为圆。

注意若求三种运动的速度之间的关系，最直接的方法是式（7-4）对时间求导，即可求出点的相对速度、牵连速度和绝对速度三者之间的关系。