点的速度和加速度的矢量表示理论力学

一般情况下，描述刚体转动时不仅应说明转动的快慢和方向，还应指明转轴在空间的方位，为此引入角速度和角加速度矢量概念。

为了指明转轴在空间的方位，规定角速度矢ω和角加速度矢α 均沿转动轴线，它们的模分别表示该瞬时刚体角速度和角加速度的大小，用k表示沿轴线Oz正方向的单位矢量，则

其指向则依据ω和α的正负号按右手螺旋法则确定，如图6-8所示。至于角速度矢和角加速度矢的起点，可在轴线上任意选取，即角速度矢和角加速度矢是滑动矢量。

当ω＞0，α＞0时，ω及α均沿Oz轴正向，说明刚体作加速转动，如图6-8 （a）所示。当ω＞0，α＜0时，ω沿Oz轴正向，而α沿负向，如图6-8 （b）所示，刚体作减速运动。

根据上述角速度和角加速度的矢量表示，刚体内任一点的速度可以用矢积表示。

如在轴线上任选一点O为原点，动点M 的矢径以r表示，如图6-9所示。那么，点M 的速度可以用角速度矢与它的矢径的矢量积表示，即

图6-8

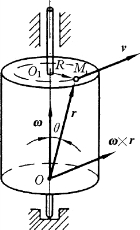
图6-9

为证明这一点，需证明矢积确实表示点M 的速度矢的大小和方向。

根据矢积的定义知，ω×r仍是一个矢量，它的大小是

式中：θ为角速度矢ω 与矢径r间的夹角。于是证明了矢积ω×r的大小等于速度的大小。

矢积ω×r的方向垂直于ω 与r所组成的平面（即图6-9中三角形OMO1 所在平面），从矢量v的末端向始端看，则见ω按逆时针转过角θ与r重合，由图容易看出矢积ω×r的方向正好与点M 的速度方向相同。

绕定轴转动的刚体上任一点的加速度矢也可用矢积表示。

因为点M 的加速度为

将v=ω×r代入，得

式 （6-19）中右端第一项的大小为

这结果恰等于点M 的切向加速度的大小，而α×r的方向垂直于α和r所组成的平面，指向如图6-10所示。这方向恰与点M 的切向加速度方向一致，因此矢积α×r等于切向加速度aτ，即

图6-10

同理可知，式 （6-19）第二项等于点M 的法向加速度，即

(www.xing528.com)

结论：

（1）作定轴转动的刚体上任意一点的速度等于角速度矢与矢径的矢量积。

（2）作定轴转动的刚体上任意一点的切向加速度等于角加速度矢与矢径的矢量积，法向加速度等于角速度与速度的矢量积。

【例6-2】 变速箱由四个齿轮构成，如图6-11所示。齿轮Ⅱ和Ⅲ安装在用一轴上，与轴一起运动，各齿轮的齿数分别为z1=36、z2=112、z3=32和z4=128，如主动轴Ⅰ的转数n1=1450r/min，试求从动轮Ⅳ的转数n4。

解：在机械中常用齿轮作为传动部件，例如本题中变速箱，是由多组齿轮构成的，起到增速和减速的作用。在齿轮相互啮合处其速度应相等。如本例中的主动轮Ⅰ和从动轮Ⅱ，设其角速度分别为ω1、ω2，齿轮的半径分别为r1 和r2，即

定义齿轮的传动比i12等于主动轮的角速度与从动轮角速度的比。

由式（a）得

由于齿轮啮合时齿距必须相等，而齿距等于齿轮节圆周长与齿轮齿数的比。若设齿轮齿数分别为z1、z2，则有

从而由式（b）和由式（c）得

即齿轮传递时，两个齿轮角速度的比等于两个齿轮半径的反比，或等于两个齿轮齿数的反比。

在机械中还有皮带轮传动，如图6-12所示。如不考虑皮带的厚度，并假设皮带与轮无相对滑动，设轮Ⅰ和轮Ⅱ的角速度分别为ω1、ω2，半径分别为r1 和r2，即

图6-11

图6-12

皮带轮的传动比i12为

即皮带轮传递时，两个皮带轮角速度的比等于两个皮带轮半径的反比。

由上面公式解本题。设四个轮的转数分别为n1、n2、n3、n4，且有

将两式相乘得

解得从动轮Ⅳ的转数n4 为