当刚体作定轴转动时,除了转轴上的各点以外,刚体上的点都在垂直于转轴的平面内作圆周运动,圆周的半径R等于该点到轴线的垂直距离,圆心在轴线上,对此,宜采用自然法研究各点的运动。
设刚体由定平面A绕定轴O 转动任一角度φ 到达B 位置,其上任一点由O′运动到M,如图6-4所示。以固定点O′为弧坐标s的原点,按φ角的正向规定弧坐标s的正向,于是当刚体转过φ角时,点M 的弧坐标为
![]()
式中:R为点M 到轴心O 的距离。
将式(6-9)对时间t取一阶导数,得

即转动刚体内任一点速度的大小,等于刚体的角速度与该点到轴线的垂直距离的乘积,它的方向沿圆周的切线而指向转动的一方。其速度分布如图6-5所示。

图6-4

图6-5
现在求点M 的加速度。因为点作圆周运动,因此应求切向加速度和法向加速度。

即转动刚体内任一点的切向加速度的大小,等于刚体的角加速度与该点到轴线垂直距离的乘积,它的方向由角加速度的符号决定。当α是正值时,它沿圆周的切线,指向角φ的正向;否则相反。
法向加速度为

式中:ρ为曲率半径,即该点到轴线的垂直距离,ρ=R,因此
![]() (https://www.xing528.com)
(https://www.xing528.com)
即转动刚体内任一点的法向加速度的大小,等于刚体角速度的平方与该点到轴线垂直距离的乘积,它的方向与速度垂直并指向轴线。如果ω与α同号,角速度的绝对值增加,刚体作加速转动,这时点的切向加速度aτ 与速度v的指向相同;如果ω与α异号,刚体作减速转动,aτ与v的指向相反。这两种情况如图6-6 (a)、(b)所示。
点M 的加速度a的大小可由下式求出
![]()
要确定加速度a的方向,只需求出a与半径MO 所成的交角θ即可,如图6-6所示。从直角三角形的关系式可得
![]()
由于在每一瞬时,刚体的ω与α都只有一个确定的数值,所以从式(6-11)、式 (6-14)和式(6-15)知:
(1)在同一瞬时,转动刚体上各点的速度v和加速度a的大小均与到转轴的垂直距离成正比。
(2)在同一瞬时,各点速度v的方向垂直于到转轴的距离R,各点加速度a的方向与到转轴的垂直距离R 的夹角θ都相等。加速度分布如图6-7所示。
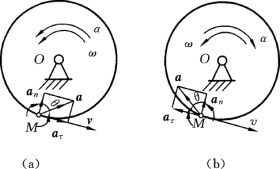
图6-6
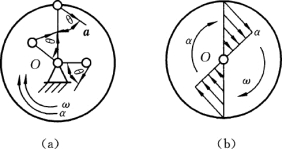
图6-7
【例6-1】 直径为d的轮子作匀速转动,每分钟转数为n。求轮缘上各点的速度和加速度。
解:根据题意,在v=Rω中代入

由于轮子作匀速转动,所以α=0,得
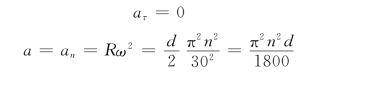
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




