点的加速度：矢量法、切向加速度、法向加速度、全加速度

由矢量法知动点的加速度为

式 （5-19）加速度应分两项，一项表示速度大小对时间变化率，用aτ 表示称为切向加速度，其方向沿轨迹曲线切线，当aτ 与v同号时动点作加速运动，反之作减速运动；另一项表示速度方向对时间变化率，用an 表示称为法向加速度。

若将动点的全加速度a向自然坐标系b、τ、n上投影，则有

式中：ab为副法向加速度。

若已知动点的切向加速度aτ和法向速度an，则动点的全加速度大小为

全加速度与法线间的夹角为

如图5-12所示。

图5-12

【例5-4】 飞轮边缘上的点按s=4sint的规律运动，飞轮的半径r=20cm。试求时间t=10s该点的速度和加速度。

解：当时间t=10s时，飞轮边缘上点的速度为

方向沿轨迹曲线的切线。

飞轮边缘上点的切向加速度为

法向加速度为

飞轮边缘上点的全加速度大小和方向为

全加速度与法线间的夹角α=0．45°

【例5-5】 已知动点的运动方程为：x=20t，y=5t2-10。式中x、y以m计，t以s计，试求t=0时动点的曲率半径ρ。

解：动点的速度和加速度在直角坐标x、y、z轴上的投影为

动点的速度和全加速度的大小为

在t=0时，动点的切向加速度为

法向加速度为

全加速度的大小为

图5-13

t=0时动点的曲率半径为

【例5-6】 半径为r的轮子沿直线轨道无滑动地滚动，如图5-13所示，已知轮心C的速度为vC，试求轮缘上的点M 的速度、加速度、沿轨迹曲线的运动方程和轨迹的曲率半径ρ。

解：沿轮子滚动的方向建立直角坐标系Oxy，初始时设轮缘上的点M 位于y轴上。在图示瞬时，点M和轮心C的连线与CH 所的夹角为

点M 的运动方程为

(www.xing528.com)

点M 的速度在坐标轴上的投影为

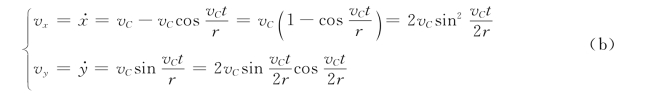
点M 的速度大小为

点M 的速度方向余弦为

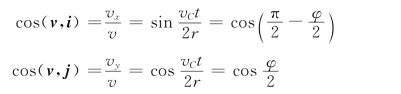
则速度的方向角为

即点M 速度沿∠MCH 角分线。

轮缘上的点M 沿轨迹曲线的运动方程，由式（c）积分得

点M 的加速度在坐标轴上的投影，由式（b）得

点M 的加速度大小和方向余弦为

则加速度的方向角为

即点M 的加速度沿MC，且恒指向轮心C点。

点M 的切向加速度和法向加速度为

轨迹的曲率半径为

讨论：

（1）点M 与地面接触时，φ=0点M 的速度v=0，即圆轮沿直线轨道无滑动地滚动时与地面接触的点的速度为零。

（2）点M 与地面接触时，点M 的加速度方向为铅直向上。

【例5-7】 列车沿半径为R=400m的圆弧轨道作匀加速运动，设初速度v0=10m/s，经过t=60s后，其速度达到v=20m/s，试求列车在t=0、t=60s时的加速度。

解：由于列车作匀加速运动，切向加速度aτ=常数，有

切向加速度为

（1）t=0时法向加速度为

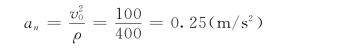
全加速度为

全加速度与法线间的夹角为

即α=45°。

（2）t=60s时法向加速度为

全加速度为

全加速度与法线间的夹角为

即α=13．6°。

描述点的运动的方法有很多，除了本章所研究的方法以外，还有极坐标、柱坐标和球坐标等，应根据所研究的问题选择适当的方法研究点的运动。例如研究行星的运动，一般选择柱坐标或者球坐标等。