同理,由式(5-3)得动点的加速度为
![]()
加速度的解析形式
![]()
则加速度在直角坐标轴上的投影为
![]()
加速度在直角坐标轴上的投影等于速度在同一坐标轴上的投影对时间一阶导数,也等于动点所对应的坐标对时间二阶导数。
若已知加速度投影,则加速度的大小和方向为

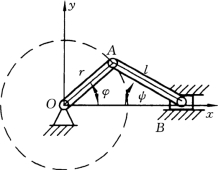
图5-5
以上是从动点作空间曲线运动来研究的,若点作平面曲线运动,则令坐标z=0;若点作直线运动令坐标y=0、z=0。
求解点的运动学问题大体可分为两类:第一类是已知动点的运动,求动点的速度和加速度,它是求导的过程;第二类是已知动点的速度或加速度,求动点的运动,它是求解微分方程的过程。
【例5-1】 曲柄连杆机构如图5-5所示,设曲柄OA长为r,绕O轴匀速转动,曲柄与x轴的夹角为φ=ωt,t为时间(单位为“s”),连杆AB长为l,滑块B在水平的滑道上运动,试求滑块B的运动方程,速度和加速度。
解:建立直角坐标系Oxy,滑块B的运动方程为
![]()
其中由几何关系得
![]()
则有

式 (b)代入式(a)得滑块B的运动方程
![]()
对式(b)求导得滑块B的速度和加速度,即

【例5-2】 已知动点的运动方程为x=rcosωt,y=rsinωt,z=ut,r、u、ω为常数,试求动点的轨迹、速度和加速度。
解:由运动方程消去时间t得动点的轨迹方程为
![]()
动点的轨迹曲线是沿半径为r的柱面上的一条螺旋线,如图5-6 (a)所示。
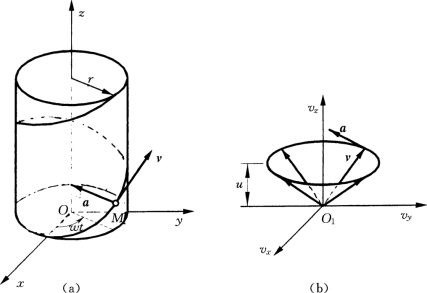
图5-6(https://www.xing528.com)
动点的速度在直角坐标轴上的投影为

速度的大小和方向余弦为
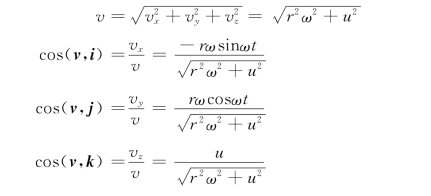
由上式知速度大小为常数,其方向与y轴的夹角为常数,故速度矢端轨迹为水平面的圆,如图5-6 (b)所示。动点的加速度在直角坐标轴上的投影为

加速度的大小和方向余弦为

则动点的加速度的方向垂直于z轴,并恒指向z轴。

图5-7
【例5-3】 如图5-7所示为液压减震器简图,当液压减震器工作时,其活塞M 在套筒内作直线的往复运动,设活塞M的加速度为a=-kv,v为活塞M 的速度,k为常数,初速度为vo,试求活塞M的速度和运动方程。
解:因活塞M 作直线的往复运动,因此建立x轴表示活塞M 的运动规律,如图5-7所示。活塞M 的速度、加速度与x坐标的关系为
![]()
代入已知条件,则有

将式(a)进行变量分离,并积分

得
![]()
活塞M 的速度为
![]()
再对式(b)进行变量分离得
![]()
积分得

得活塞M 的运动方程为
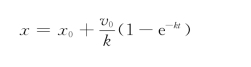
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




